
Taylor Series Formula: A Taylor Series is a representation of a function as an infinite sum of terms, where each term is expressed in terms of the function's derivatives at a specific point. The Taylor series formula allows us to approximate a function by summing an infinite series of terms, where each term is related to the function's value and its derivatives at a chosen point.
What Is Taylor Series Formula?
The Taylor series formula you provided is indeed an accurate representation of the Taylor series expansion for a function f(x) around a point a. This formula shows how you can express a function as an infinite sum of terms, where each term is related to the function's value and its derivatives at the point a. It's a powerful mathematical tool for approximating functions and is widely used in various areas of mathematics and science.
Here's a breakdown of the key components in the formula:
![]()
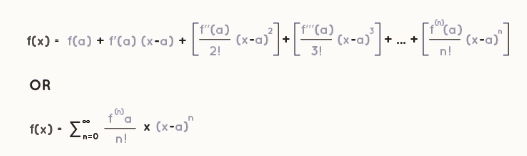
f(x): The function you want to approximate.
f(a): The value of the function at the center point a.
f'(a): The first derivative of the function at a.
f''(a): The second derivative of the function at a.
f'''(a): The third derivative of the function at a.
(x - a): The difference between the variable x and the center point a.
n: The total number of terms in the series, which can be infinite in a full Taylor series expansion.
The formula you provided is a concise way to express the Taylor series, where the terms in the series are built using the function and its derivatives at the center point a. The sum of these terms, up to n terms, provides an approximation of the function within a certain range around a. As you include more terms (i.e., increase n), the approximation becomes more accurate within that range. However, it's essential to consider the radius of convergence to ensure that the series converges to the function within a specific interval around the center point.
The second representation you provided is a compact way to express the Taylor series using sigma notation (∑) and the factorial (n!) notation. It's a concise way to represent the sum of all the terms in the series.
In both representations, the Taylor series is a powerful tool for approximating functions and solving various mathematical and scientific problems.
Taylor Series Formula Proof
Taylor's Series Theorem Statement:
Assume that if f(x) be a real or composite function, which is a differentiable function of a neighbourhood number that is also real or composite. Then, the Taylor series describes the following power series:
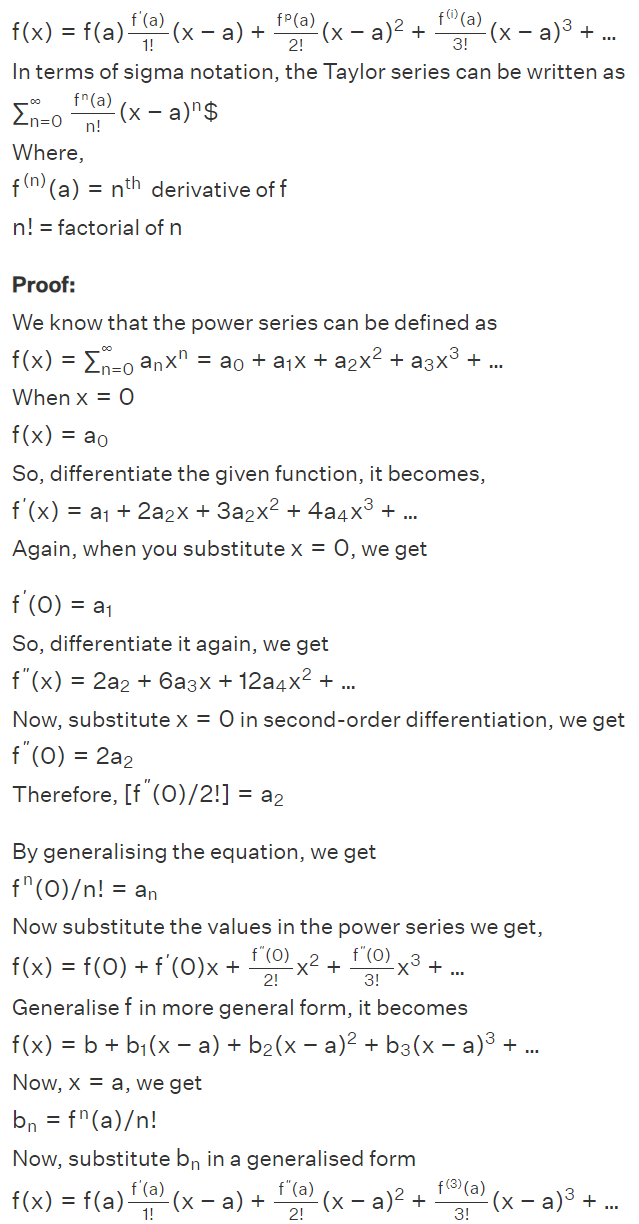
Application of Taylor Series Formula
The Taylor series is a powerful mathematical tool with numerous applications in mathematics, science, engineering, and many other fields. Here are some of the common applications of the Taylor series formula:
- Function Approximation: One of the most fundamental applications is to approximate a function by using a finite number of terms in its Taylor series. This can be especially useful when dealing with complex functions, and it allows for simpler calculations.
- Calculus and Analysis: The Taylor series can be used to find derivatives and integrals of functions, making it a valuable tool in calculus and mathematical analysis.
- Physics: In physics, the Taylor series is used to approximate various physical phenomena. For example, it is used in the study of oscillations, waves, and particle motion.
- Engineering: Engineers often use Taylor series to approximate the behavior of systems in control theory, electrical circuits, and structural analysis. It is also used for signal processing and filter design.
- Economics and Finance: In economics and finance, Taylor series can be used to approximate complex economic models and make predictions about future trends or market behavior.
- Computer Graphics: Taylor series is used in computer graphics to approximate functions for rendering and animation. It helps create realistic images and animations in video games and simulations.
- Probability and Statistics: In statistics, the Taylor series can be employed to approximate probability density functions, cumulative distribution functions, and moments of random variables.
- Numerical Methods: The Taylor series is the foundation for many numerical methods used in solving equations, root finding, and optimization problems.
- Quantum Mechanics: In quantum mechanics, Taylor series is used to approximate solutions to Schrödinger's equation, which describes the behavior of quantum systems.
- Machine Learning: In some machine learning algorithms, Taylor series expansions are used to approximate complex functions and make predictions based on a series of simpler approximations.
- Error Analysis: Taylor series is employed in error analysis, helping to estimate the accuracy of numerical methods and calculations.
- Waveform Analysis: In signal processing and communications, the Taylor series is used to analyze and approximate waveforms.
These are just a few examples of the many applications of the Taylor series formula. Its versatility and power make it a fundamental concept in mathematics and various scientific disciplines, providing a means to represent and understand complex functions and phenomena.
Examples Using Taylor Series Formula
Example 1: For the function f(x) = 2x - 2 x 2 centered at a = -3:
The Taylor series expansion is: -24 + 14(x + 3) - 2(x + 3) 2
Example 2: For the function f(x) = cos(x) centered at a = 0:
The Taylor series expansion is: 1 - x 2 /2! + x 4 /4! - ...
Example 3: For the function f(x) = x 3 - 10x 2 + 6 centered at x = 3:
The Taylor series expansion is: -57 - 33(x - 3) - (x - 3) 2 + (x - 3) 3
These expansions provide a way to approximate the functions around the given points, with the number of terms determining the level of accuracy within a certain radius of convergence. Well done on applying the Taylor series formula to these examples!
| Related Links | |
| Covariance Formula | Decay Formula |
| Cp Formula | Derivative Formula |
Taylor Series Formula FAQs
Q1. What is the Taylor series formula used for?
Q2. How is the Taylor series different from the Maclaurin series?
Q3. What is the radius of convergence in a Taylor series?
Q4. Can the Taylor series be used to approximate any function?
Q5. How do you determine the number of terms to use in a Taylor series expansion?










