Determinants
are scalar values derived by summing the products of elements within a square matrix and their respective cofactors, following a specific rule. Determinants play a crucial role in various mathematical operations, such as finding the adjoint and inverse of a matrix. They are also essential in solving systems of linear equations using the matrix inversion method. Additionally, determinants aid in understanding and calculating the cross-product of two vectors.
What Are Determinants?
Determinants serve as scaling factors for matrices, representing how they stretch or shrink. They encapsulate the concept of transformations applied to matrices, measuring their effect on size. Determinants are mathematical functions that take a square matrix as input and yield a single numeric value as their output.
Determinants Definition
For any square matrix, denoted as C with elements cij in an n×n order, we can define a determinant as a single scalar value, which can be either a real or a complex number. In this context, cij represents the element located at the (i, j) position within matrix C. The determinant is typically represented as det(C) or |C|, where the notation |C| is used to express the determinant by enclosing it within absolute-value bars, as opposed to square brackets.
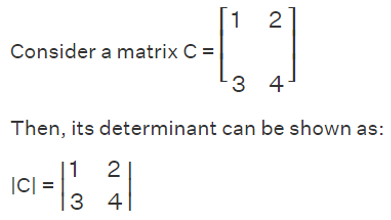
How To Calculate Determinant?
In the case of the simplest square matrix, which is a 1×1 matrix containing only one number, the determinant is equal to that single number itself. Now, let's explore how to compute determinants for square matrices of higher orders, including second-order, third-order, and fourth-order matrices.
Calculating Determinant of 2x2 Matrix
To compute the determinant of a 2x2 square matrix or a square matrix of order 2×2, we can utilize the following determinant formula:
Also Check –
Area related to circles Formula
Calculating Determinant of 3x3 Matrix
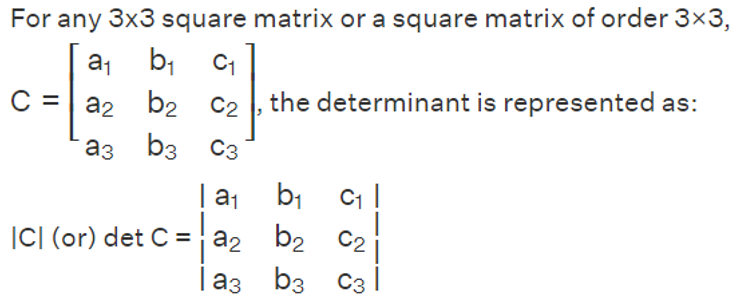
Here are the steps involved in calculating the determinant of a 3x3 matrix:
Choose an anchor element, for example, a1, from the first row of the matrix.
Calculate the determinant of the 2x2 sub-matrix (known as the minor) obtained by removing the current row and column that contain the anchor element (in this case, the minor of a1).
Repeat the above step for the other two anchor elements, b1 and c1, located in the first row.
Multiply each of the minor determinants by their respective anchor elements (a1, b1, c1).
Sum up the products obtained in the previous step to find the determinant of the 3x3 matrix.
This process allows you to compute the determinant of a 3x3 matrix by breaking it down into smaller sub-matrices and applying a specific pattern of multiplication and addition involving the anchor elements and their corresponding minors.
Also Check –
Linear Inequalities formula
It's important to note that while we calculated the determinant of a 3x3 matrix using the elements from the first row in the example, you can use any row or any column to calculate the determinants following the same approach. The choice of which row or column to use does not affect the result; you will obtain the same determinant value regardless of the selection.
Calculating the Determinant of a 4×4 Matrix
When finding the determinant of a 4x4 square matrix (or a square matrix of order 4×4), there are certain important considerations to keep in mind:
-
Expanding along a Row or Column:
Just as with smaller matrices, you can expand the determinant along any row or column. This means you can choose the row or column that makes the calculations more convenient for you.
-
Cofactor Expansion:
To find the determinant of a 4x4 matrix, you can use the method of cofactor expansion. It involves breaking down the matrix into 3x3 sub-matrices, calculating their determinants, and combining them following a specific pattern of signs and multiplication.
-
Pattern of Signs:
In the cofactor expansion method, the pattern of signs alternates between positive and negative as you move across the matrix. The standard pattern is often remembered as "+ - + -" or vice versa. It's essential to apply the correct sign to each term in the expansion.
-
Multiple Expansions:
You may choose to expand the determinant along a row or column that contains elements with zeros, as this can simplify the calculations. Additionally, you can select the row or column that results in the fewest non-zero terms when calculating the sub-matrices.
-
Computational Efficiency:
When calculating determinants of larger matrices, it's helpful to use a method or strategy that minimizes computational effort. Selecting the appropriate row or column for expansion and optimizing your calculations can save time and reduce the chance of errors.
By keeping these considerations in mind and following the rules of determinant calculation, you can efficiently find the determinant of a 4x4 matrix.
Also Check –
Cube Root Formula
Multiplication of Determinants
We employ a method known as the multiplication of arrays to multiply two determinants of square matrices. Specifically, we can use the row-by-column multiplication rule to multiply the determinants of square matrices A and B:
Properties of Determinants
In the calculation of determinants for square matrices of various types, these determinants are determined based on crucial properties. Here is a list of some important properties of determinants:
Property 1:
"The determinant of an identity matrix is always equal to 1."
Property 2:
"If any square matrix B with order n×n has a zero row or a zero column, then det(B) = 0"
Property 3:
"If C is upper or a lower-triangular matrix then det(C) is the product of all its diagonal entries"
Property 4:
"If D is a square matrix, then if its row is multiplied by a constant k, then the constant can be taken out of the determinant"
Also Check –
Real Number Formula
Rules For Operations on Determinant
Here are some essential rules that are useful when performing row and column operations on determinants:
The value of the determinant remains unchanged if the rows and columns are interchanged.
The sign of the determinant changes if any two rows or columns are interchanged.
If any two rows or columns of a matrix are equal, then the value of the determinant is zero.
If every element of a particular row or column is multiplied by a constant, then the value of the determinant is also multiplied by that constant.
If the elements of a row or a column are expressed as a sum of elements, then the determinant can be expressed as a sum of determinants.
If the elements of a row or column are added or subtracted with the corresponding multiples of elements of another row or column, then the value of the determinant remains unchanged.
Important Notes on Determinant
Here are some key points to keep in mind when studying determinants:
A determinant can be viewed as a mathematical function that takes a square matrix as its input and yields a single numeric value as its output.
A square matrix is defined as a matrix with an equal number of rows and columns, resulting in a grid-like structure.
In the case of the simplest square matrix, which is a 1×1 matrix containing only one number, the determinant value is equal to the number itself.
