
Vector Projection Formula: The projection vector illustrates the component of one vector onto another. It denotes a scalar quantity, acquired by multiplying the specified vector by the sine of the angle between the two vectors.
The concept of vector projection finds extensive use in physics and engineering, particularly in representing a force vector concerning another vector. Exploring the vector projection formula, its derivation, and examining various examples can provide a deeper understanding.
What is a Projection Vector?
The vector projection of one vector onto another is the magnitude of the projection of the given vector onto the other. This is achieved by multiplying the magnitudes of the respective vectors by the cosecant of the angle between them. The outcome of the vector projection formula results in a scalar value. The projection of vector → a onto vector → b is determined by multiplying vector a by the cosecant of the angle between vectors a and b. This calculation simplifies to derive the final value of the projection vector. The projection vector possesses a magnitude that is a component of the magnitude of vector a and shares the same direction as vector b.
Vector Projection Formula
In vector algebra, the formula for the projection of vector a onto vector b involves taking the dot product of vector a and vector b, then dividing it by the magnitude of vector b. The dot product yields a scalar value, as does the magnitude of vector b. Consequently, the magnitude and direction of the projection vector's answer also end up as a scalar value, aligned with the direction of vector b.
Vector Projection Formula
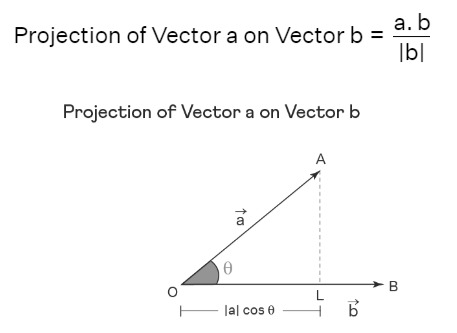
Deriving the Formula for Projection Vector
The derivation process elucidates and enables a clearer comprehension of the projection vector formula, which signifies the projection of one vector onto another. Consider two vectors, labeled OA = → a and OB = → b, with θ representing the angle between → a and → b. This derivation focuses on determining the component of vector a along vector b. Visualize drawing AL perpendicular to OB.
From the right triangle OAL , cos θ = OL/OA
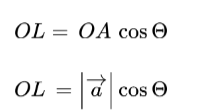
OL is the projection vector of vector a on vector b.
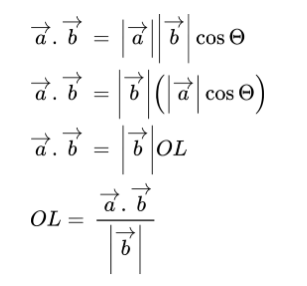
Thus, projection vector formula of of vector a on b
Vector Projection Formula
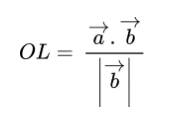
Relation of Projection Vector
The subsequent concepts presented below aid in enhancing comprehension of the projection vector. Let's discuss the details, encompassing the formula to determine the angle between two vectors and the computation of the dot product of these vectors.
Calculation of the Angle Between Two Vectors
The angle between two vectors is computed using the cosine function. Specifically, it is determined by taking the inverse cosine of the dot product of the individual components of the vectors, divided by the product of the magnitudes of the two vectors. The formula for the angle between two vectors is expressed as follows:
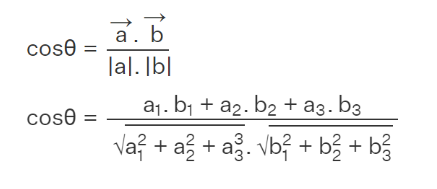
Dot Product of Two Vectors
The dot product, synonymous with the scalar product, refers to the mathematical operation conducted between two vectors. When these vectors are represented using unit vectors—i, j, k—aligned with the x, y, z axes, the scalar product can be determined in the following manner:
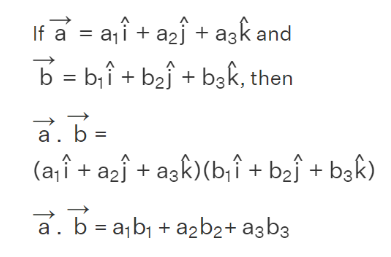
The vector projection is a fundamental concept in mathematics, physics, and engineering that defines the projection of one vector onto another. It involves calculating a scalar quantity, obtained by multiplying the specific vector by the sine of the angle between the vectors. This concept is extensively applied in various fields, particularly in representing force vectors concerning other vectors.
The formula for vector projection, derived from the dot product and vector magnitudes, allows us to determine the component of one vector along another. Through this process, the projection vector yields a scalar value, sharing the same direction as the vector onto which it's projected.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| Recursive Formula | Regular Square Pyramid Formula |
| Vieta’s Formula | Quartile Formula |
Vector Projection Formula FAQs
What is a vector projection?
How is the projection vector calculated?
What does the magnitude of the projection vector signify?
In what fields is vector projection used?










