The
Volume of a Cube Formula
signifies the quantity of cubic units completely occupied by the cube. It is measured in cubic units, such as centimeters³, meters³, inches³, feet³, and so on. A cube is a solid three-dimensional geometric figure composed of six square faces or sides. Consequently, the volume of a cube represents the entirety of space enclosed by it. Since all the faces of the cube are square in shape, the lengths of its edges are also equal. Therefore, if the length, width, and height of the cube are equal, denoted as 'a,' then the Volume of a Cube Formula.
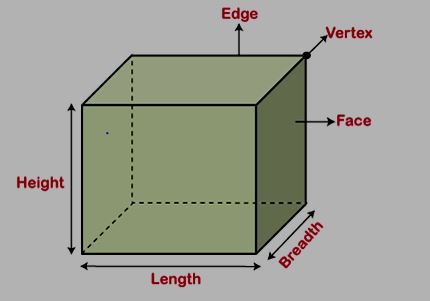
Volume = Length ×Height × Breadth
If , Length = Height = Breadth = a
Volume of Cube = a × a × a =
a
3
Edge:
An edge is defined as a line segment that connects two vertices. A cube has a total of twelve edges, all of which are of equal length.
Face:
The faces of a cube are the square surfaces that make up its sides. In a cube, there are six faces: the top, bottom, right, left, front, and back faces.
Vertex:
A vertex is a point where three edges intersect. A cube has a total of eight vertices.
Also Check -
Introduction to Graph Formula
Surface Area of a Cube
The surface area of a cube is the total of the areas of its external surfaces. To determine the surface area of a cube, which is the number of square units covering the entire surface of the cube, we use the following general formula for a cube with side length 'a':
Surface Area of Cube = 6a²
Also Check -
Comparing Quantities Formula
Illustrating Volume of a Cube with Examples
Example 1:
Determine the cube's volume when its sides measure 7 cm each.
Solution:
Given the side length of the cube is 7 cm.
We know that the volume of a cube is given by (side length of the cube)³.
Therefore, Volume, V = (7 cm)³
V = 343 cm³
Example 2:
Find the edge length of a cube when its volume measures 125 cm³.
Solution:
Given the volume of the cube is 125 cm³.
Let 'a' represent the length of the edges.
Using the formula for the volume of a cube, we have:
125 = a³
Calculating the cube root of both sides:
a = ³√125
a = 5 cm
Hence, the length of the cube's edges is 5 cm.
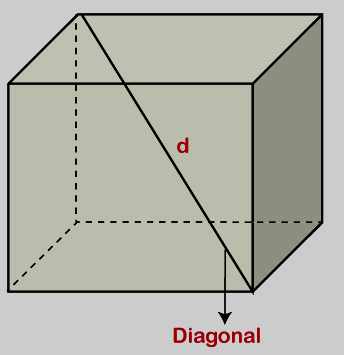
Example 3:
Find the volume of a cube with a diagonal length of 27 cm.
Solution:
Using the formula for the volume of a cube given its diagonal, we have:
Volume = √3 × d³/9
Given that d = 27 cm,
Volume of the cube = √3 × (27 × 27 × 27)/9
= √3 × (27 × 27 × 3)
≈ 3788 cubic units
Therefore, the volume of the cube is approximately 3788 cubic units.
Also Check -
Linear Equation Formula
Example 4:
Determine the volume of a cube if the length of one of its edges is 10 inches.
Solution:
Given the edge length of the cube is 10 inches.
Utilizing the formula for the cube's volume:
Volume = (edge length)³
Volume = (10 inches)³
Volume = 1,000 cubic inches
So, the volume of the cube is 1,000 cubic inches.
Example 5:
Find the length of the edges of a cube if its volume is 64 cubic centimeters.
Solution:
Given the volume of the cube is 64 cubic centimeters.
Let 'a' represent the length of the edges.
Utilizing the formula for the cube's volume:
64 = a³
Calculating the cube root of both sides:
a = 4 centimeters
Hence, the length of the cube's edges is 4 centimeters.
Also Check -
Rational Number Formula
Example 6:
Calculate the surface area of a cube with an edge length of 6 meters.
Solution:
Given the edge length of the cube is 6 meters.
Here we using formula for the surface area of a cube:
Surface Area = 6 × (edge length)²
Surface Area = 6 × (6 meters)²
Surface Area = 6 × 36 square meters
Surface Area = 216 square meters
So, the surface area of the cube is 216 square meters.
Example 7:
Find the volume of a cube if the sum of the lengths of its edges is 48 units.
Solution:
Given the sum of the lengths of the cube's edges is 48 units.
Let 'a' represent the length of one edge.
Since there are 12 edges on a cube, the sum of the lengths of the edges can be expressed as:
12a = 48
Dividing both sides by 12:
a = 4 units
Now, using the formula for the volume of a cube:
Volume = (edge length)³
Volume = (4 units)³
Volume = 64 cubic units
So, the volume of the cube is 64 cubic units.
