Volume of a Hemisphere Formula: Definition, Solved Examples

Volume of a Hemisphere Formula are field of geometry, we explore various three-dimensional shapes, each characterized by three distinct measurements: length, breadth, and height. These three-dimensional objects do not exist solely on a flat surface and are often derived from the rotation of two-dimensional shapes.

One exemplary 3D shape is the sphere, which originates from the rotation of a 2D shape known as a circle. An apt real-world example of a sphere is our planet Earth, which exhibits a spherical form.

Also Check - Line and Angles Formula

Hemisphere Definition

A sphere is defined as a collection of points in three dimensions, with all points on its surface equidistant from the center. When a plane intersects the sphere at its center, dividing it into two equal parts, it forms what we call a hemisphere. A hemisphere essentially constitutes half of a sphere. Generally, a sphere gives rise to two hemispheres. An illustrative example is Earth, consisting of the Southern Hemisphere and the Northern Hemisphere.

Also Check - Logarithm Formula

Hemisphere Volume

Calculating the volume of a hemisphere is straightforward, given that the sphere's base is circular. The formula for the volume of a hemisphere was developed by Archimedes and is as follows:

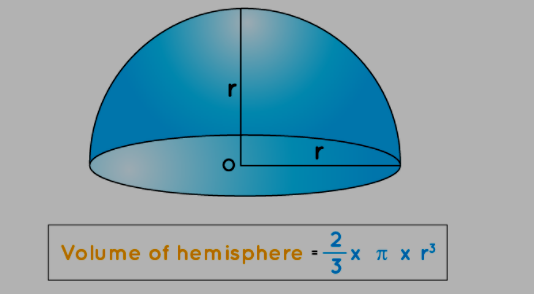
The volume of a hemisphere = (2/3)πr³ cubic units.

Here, π represents a constant with an approximate value of 3.14, and "r" signifies the radius of the hemisphere.

Download PDF Volume of a Hemisphere Formula

Also Check - Comparing Quantities Formula

Hemisphere Equation

When the radius "R" is centered at the origin, the equation for a hemisphere is expressed as:

x² + y² + z² = R²

In the Cartesian form or equation of a hemisphere with radius "R" at the point (x₀, y₀, z₀), it is represented as:

(x - x₀)² + (y - y₀)² + (z - z₀)² = R²

The spherical coordinates of the hemisphere are defined as follows:

x = r cos θ sin ∅

y = r sin θ cos ∅

z = r cos ∅

Examples

Example : Calculate the volume of a hemisphere with a radius of 12 cm.

Solution: Given: Radius, r = 12 cm

Using the formula for hemisphere volume:

V = (2/3)πr³ cubic units

Substituting the value of r into the formula:

V = (2/3) × 3.14 × 12 × 12 × 12

V = 2 × 3.14 × 4 × 12 × 12

V = 3617.28

Therefore, the volume of the hemisphere is 3617.28 cubic units.

Example  : Calculate the volume of a hemisphere with a radius of 9 cm.

Solution: Given: Radius, r = 9 cm

Using the formula for hemisphere volume:

V = (2/3)πr³ cubic units

Substituting the value of r into the formula:

V = (2/3) × 3.14 × 9 × 9 × 9

V = 2 × 3.14 × 3 × 9 × 9

V = 1526.04

Therefore, the volume of the hemisphere is 1526.04 cubic units.