CBSE Worksheet for Chapter - 9 Line and Angles Class 8

CBSE Worksheet for Chapter - 9 Line and Angles Class 8

Worksheets For class 8

Find CBSE Worksheet for chapter-9 Line and Angles class 8

CLASS-8

BOARD: CBSE

Mathematic Worksheet - 9

TOPIC: Line and Angles

For other CBSE Worksheet for class 8 Mathematic check out main page of Physics Wallah.

SUMMARY:



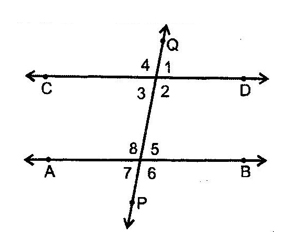
1. Transversal: A line which intersects two or more given parallel lines at distinct points is called a transversal of the given lines.

2. Corresponding angles: ∠1 & ∠ 5, ∠ 4 & ∠ 8, ∠ 2 & ∠ 6, ∠ 3 & ∠ 7 are pairs of corresponding angles.

3. Alternate interior angles: ∠ 3 &  ∠ 5, ∠ 2 & ∠ 8 are the pairs of alternate interior angles.

4. Consecutive interior angles: ∠ 2 &  ∠ 5, ∠ 3 &  ∠ 8, are pairs of consecutive interior angles.

5. Vertically opposite angles: in figure, ∠ 1 = ∠ 3, ∠ 2 = ∠ 4, ∠ 5 = ∠ 7 & ∠ 6 = ∠ 8.

OBJECTIVE:

1. Two supplementary angles are in ratio 4 : 5, then the angles are:

(A) 80°, 100°

(B) 70°, 110°

(C) 80°, 120°

(D) None

2. If an angle differs from its complement by 10°, find the larger angle.

(A) 45°

(B) 50°

(C) 95°

(D) 60°

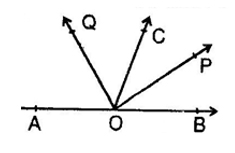
3. In the given figure, OP and OQ bisect ∠ BOC and ∠ AOC respectively, then ∠ POQ is.

(A) 90°

(B) 45°

(C) 135°

(D) 180°



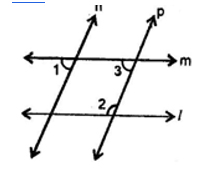
4. In the given fig if l II m, n II p and ∠1 = 85° then ∠ 2 is

(A) 95°

(B) 110°

(C) 135°

(D) 85°



5. An larger angle is 14° more than its complementary angle then angle is:

(A) 38°

(B) 52°

(C) 50°

(D) none of these

6. X lies in interior of ∠BAC. If ∠BAC = 70° and ∠BAX = 42° then ∠XAC = ?

(A) 28°

(B) 29°

(C) 27°

(D) 30°

7. If the supplement of an angle is three times its complement, then angle is:

(A) 40°

(B) 35°

(C) 50°

(D) 45°

8. Two angles whose measures are a & b are such that 2a – 3b = 60°, if they form a linear pair then find 4a/5b.

(A) 0

(B) 8/5

(C) 1/2

(D) 2/3

9. The supplement of an angle is one third of itself. Then the angle is:

(A) 135°

(B) 45°

(C) 140°

(D) None

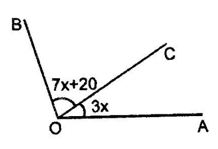
10. In given figure, if ∠BOC = 7x + 20° and ∠COA = 3x, then the value of x for which AOB becomes a straight line.

(A) 15°

(B) 12°

(C) 16°

(D) None



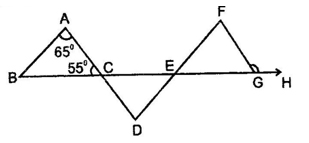
11. In given figure if AB II DF, AD II FG ∠BAC = 65°, ∠ACB=55 ^o ∠FGH is:

(A) 120°

(B) 125°

(C) 115°

(D) 140°



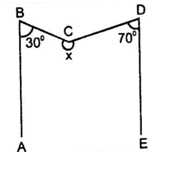
12. In given figure, AB II ED and ∠ABC = 30°, ∠EDC = 70° then x is:

(A) 240°

(B) 125°

(C) 260°

(D) None



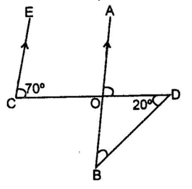
13. In the given figure, if EC II AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is-

(A) 20°

(B) 50°

(C) 60°

(D) 70°



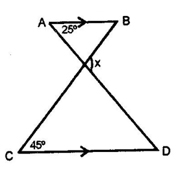
14. Given AB II CD, x° =

(A) 20°

(B) 70°

(C) 110°

(D) 35°



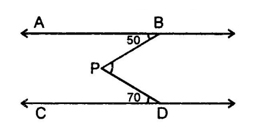
15. As shown in the figure 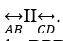. If point P is between these two lines such that m∠ABP = 50° and m∠CDP = 70° then find ∠BPD.

(A) 120°

(B) 70°

(C) 110°

(D) 50°



16. The measure of that angle which is four times its supplement is:

(A) 36

(B) 144°

(C) 155°

(D) 180°

Solutions: to worksheet-9 Topic- Line and Angles

Objective:

1) A

2) B

3) A

4) A

5) B

6) A

7) D

8) B

9) A

10) C

11) B

12) C

13) B

14) B

15) A

16) B