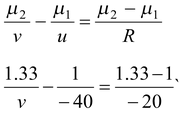Refraction on Curved Surfaces
Optics of Class 12
Refraction on Curved Surfaces
|
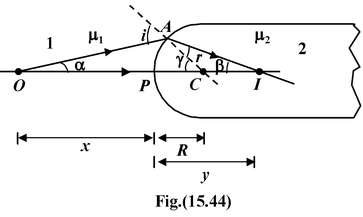
Consider a spherical surface of radius R separating the two media 1 and 2 as shown in figure. A point object O is placed on the principal axis and we have to find the position of its image I from the pole P of the boundary surface. Using geometry, we have i = α + γ (i) andγ = r + β (ii) From Snell’s law μ 1 sin i = μ 2 sin r |
|
Applying paraxial approximation : sin i ≈ i and sin r ≈ r
Thusμ 1 i = μ 2 r
Eliminating i and r from equation (i) and (ii), we get
μ 1 α + μ 2 β = (μ 2 - μ 1 )γ
Since α ≈ AP/x ;β = AP/y ;γ = AP/R
∴
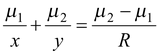
Applying Cartesian Sign Convention the above equation may be obtained from the general formula given as:
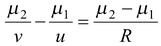 (15.20)
(15.20)
whereu is the position of the object from the pole
v is the position of the image from the pole
R is the radius of curvature of the surface
μ 1 is the medium which comes before the boundary, and
μ 2 is the medium which comes after the boundary if we move in the direction of the incident light.
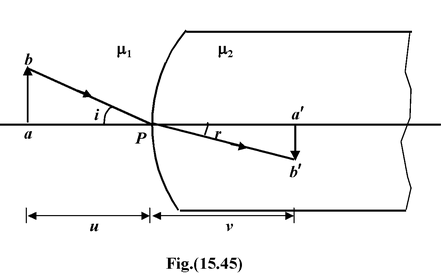
Lateral Magnification for Refracting Spherical Surface
|
Magnification is defined as m = height of image/height of object Using Cartesian convention, m = -a'b'/ab From Snell’s law, we know that μ 1 sin i = μ 2 sin r Applying paraxial ray assumption sin i ≈ i and sin r ≈ r Thus μ 1 i = μ 2 r or r/i = μ 1 /μ 2 Alsoab = ui and a′b′ = vr Thusm = -vr/ui |
|
Substituting the value of (r/i) , we get
m =
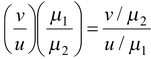 (15.21)
(15.21)
Example 15.13
|
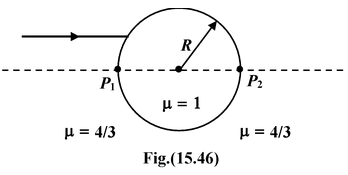
A parallel beam of light travelling in water (μ = 4/3 ) is refracted through a spherical air bubble of the final image formed. (a)Find the position of the final image formed. (b) Draw the ray diagram |
|
Solution
(a)Refraction at the first surface:
u = -∞ ; μ 1 = 4/3 ; μ 2 = 1; R = +R
Using the equation (15.20)
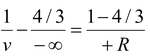
orv = -3R
The image is at a distance 3R from P 1 in water.
Refraction at the second surface.
μ 2 = 4/3 ; μ 1 = 1; u = -(3R + 2R) = -5R; R = -R
∴
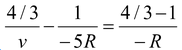
or v = -5R/3
The final image is at a distance 5R/2 from P 2 towards left, as shown in the figure.
(b)
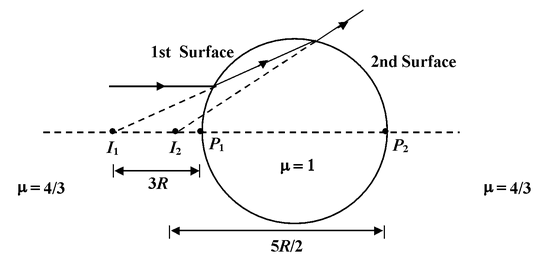
Example 15.14
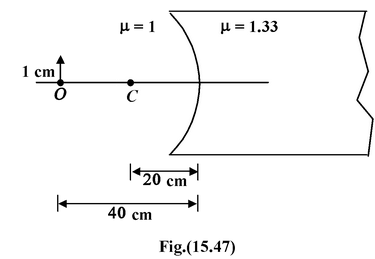
For the optical arrangement shown in the figure.
Solution
|
According to Cartesian sign convention u = -40cm, R = -20 cm μ = 1, μ 2 = 1.33 Applying equation (15.2), we get
|
|
After solving, v = -32 cm.
The magnification is m =
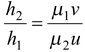
∴
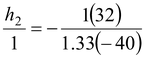 orh
2
= 0.6 cm
orh
2
= 0.6 cm
The positive sign shows that the image is erect.
Related Topics