
CBSE Class 7 Maths Notes Chapter 11 Perimeter and Area: In CBSE Class 7 Maths, Chapter 11 tells about Perimeter and Area, which are important concepts in geometry. Perimeter means the total length around the edge of a shape, while area is the space inside the boundaries of a shape. Knowing these ideas well is important because they help us understand shapes better.
In this chapter, students will learn how to find the perimeter and area of different shapes like squares, rectangles, triangles, and circles using specific formulas. They'll also see how these concepts are used in real life. By learning these things, students will become better at understanding shapes and solving problems related to them.CBSE Class 7 Maths Notes Chapter 11 Perimeter and Area PDF
You can access the CBSE Class 7 Maths Notes for Chapter 11 on Perimeter and Area by clicking on the PDF link provided below. The notes provide explanations, examples, and exercises to help students learn and practice these concepts effectively.CBSE Class 7 Maths Notes Chapter 11 Perimeter and Area PDF
CBSE Class 7 Maths Notes Chapter 11 Perimeter and Area
Perimeter
Perimeter refers to the total length or distance covered along the boundary of a closed shape, such as a square, rectangle, triangle, or any other polygon. It's like tracing the outline of a shape. The perimeter is calculated by adding up the lengths of all the sides of the shape. For example, the perimeter of a square with sides of length 5 meters would be 5 + 5 + 5 + 5 = 20 meters. Similarly, the perimeter of a rectangle with length 8 meters and width 6 meters would be 8 + 8 + 6 + 6 = 28 meters. In simple terms, the perimeter is the distance around the edge of a shape.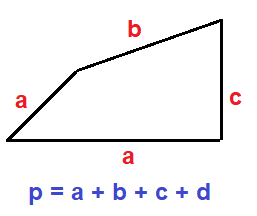
Area
Area refers to the amount of space enclosed within the boundary of a two-dimensional shape, such as a square, rectangle, circle, triangle, or any other polygon. It's like the surface area or space covered by the shape. The area is calculated differently depending on the shape. For example, the area of a square is found by multiplying the length of one side by itself (squared). So, if a square has sides of length 5 meters, its area would be 5 meters multiplied by 5 meters, which equals 25 square meters. Similarly, the area of a rectangle is found by multiplying its length by its width. For instance, if a rectangle has a length of 8 meters and a width of 6 meters, its area would be 8 meters multiplied by 6 meters, which equals 48 square meters. In simple terms, the area is the measure of the space inside a shape.
The perimeter of Square and Rectangle
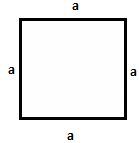
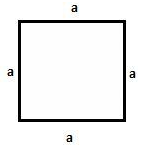
- Perimeter of a square = a + a + a + a = 4a, where a is the length of each side.
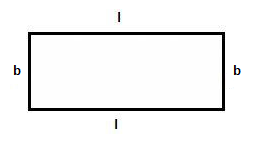
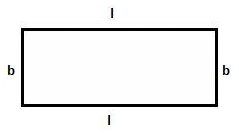
- Perimeter of a rectangle = l + l + b + b = 2(l + b), where l and b are length and breadth, respectively.
Area of Square & Rectangle
Area of square = 4 a 2Here a is the length of each side
Area of rectangle = Length(l) × Breadth(b) = l × b
Area of a Parallelogram

- Area of parallelogram ABCD = ( b a s e × h e i g h t )
Area of parallelogram ABCD = ( b × h )
Triangle as Part of Rectangle
- The rectangle can be considered as a combination of two congruent triangles.
-
Consider a rectangle ABCD, it is divided into 2 triangles ACD and ABD.

Triangles as parts of Rectangle - Area of each triangle = 1 2 (Area of the rectangle). = 1 2 ( l e n g t h × b r e a d t h ) = 1 2 ( 10 c m × 5 c m ) = 25 c m 2
Area of a Triangle
- Consider a parallelogram ABCD.
- Draw a diagonal BD to divide the parallelogram into two congruent triangles.
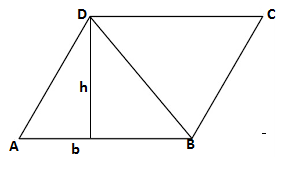
- Area of triangle ABD = 1/2 (Area of parallelogram ABCD)
| CBSE Syllabus Class 7 | |
| CBSE Class 7 English Syllabus | CBSE Class 7 Math Syllabus |
| CBSE Class 7 Social Science Syllabus | CBSE Class 7 Science Syllabus |
Conversion of Units
- Kilometres, metres, centimetres, millimetres are units of length.
- 10 millimetres = 1 centimetre
- 100 centimetres = 1 metre
- 1000 metres = 1 kilometre
Terms Related to Circle
- A circle is a simple closed curve which is not a polygon.
- A circle is a collection of points which are equidistant from a fixed point .

- The fixed point in the middle is called the centre .
- The fixed distance is known as radius .
- The perimeter of a circle is also called as the circumference of the circle.
Circumference of a Circle
- The circumference of a circle ( C ) is the total path or total distance covered by the circle. It is also called a perimeter of the circle.
Circumference of a circle = 2 × π × r ,where r is the radius of the circle.
Visualising Area of a Circle
Area of Circle
- Area of a circle is the total region enclosed by the circle.
Area of a circle = π × r 2 , where r is the radius of the circle.
Introduction and Value of Pi
- Pi ( π ) is the constant which is defined as the ratio of a circle’s circumference ( 2 π r ) to its diameter(2r) .
π = Circumference ( 2 π r )/Diameter (2r)
- The value of pi is approximately equal to 3.14159 or 22/7.
Cost of Framing, Fencing
- Cost of framing or fencing a land is calculated by finding its perimeter.
- Example: A square-shaped land has length of its side 10m. Perimeter of the land = 4 × 10 = 40m Cost of fencing 1m = Rs 10 Cost of fencing the land = 40 m × Rs 10 = Rs 400
Cost of Painting, Laminating
- Cost of painting a surface depends on the area of the surface.
- Example: A wall has dimensions 5 m × 4 m . Area of the wall = 5 m × 4 m = 20 m 2 Cost of painting 1 m 2 of area is R s 20 . Cost of painting the wall = 20 m 2 × R s 20 = R s 400
Related Links -
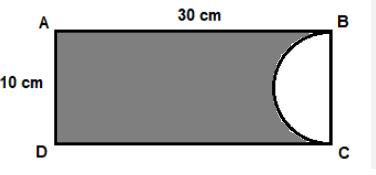
Area of Mixed Shapes
- Find the area of the shaded portion using the given information.
CBSE Class 7 Maths Notes Chapter 11 FAQs
What is the difference between perimeter and area?
Perimeter refers to the total distance around the boundary of a closed figure, while area is the measure of the total surface enclosed by the figure.
Can the area of irregular shapes be calculated?
Yes, the area of irregular shapes can be calculated by breaking them down into smaller, regular shapes (like rectangles or triangles), finding the area of each part, and then adding them together.
What units are used to measure perimeter and area?
Perimeter is measured in linear units such as meters, centimeters, or feet, while area is measured in square units such as square meters, square centimeters, or square feet.
How is the perimeter used in real-life situations?
Perimeter is used in various real-life scenarios, such as calculating the length of fencing required for a garden, the distance around a track, or the circumference of circular objects like tires or lids.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App







