CBSE Class 7 Maths Notes Chapter 8
CBSE Class 7 Maths Notes Chapter 8:
Due to its many practical applications, CBSE Class 7 Maths Notes Chapter 8 Comparing Quantities is a crucial chapter in the NCERT Math textbook for students. Students can better grasp the key subjects that make up the majority of the questions in the Class 7 exam by using the revision notes for Mathematical Chapter 8.
CBSE Class 7 Maths Notes Chapter 8 of Comparing Quantities is a useful resource for students preparing for the coming Olympiad exam, as one or two problems from this chapter typically appear on the test.
To get subject-best grades, download the NCERT Solutions PDF and choose to cross-refer after answering questions. If you have access to the NCERT Solution for Class 7 Science, studying subjects like science, math, English, social science, and Hindi will become simpler. NCERT Solutions for Class 7 Maths are also available for download, which will assist you in reviewing the entire syllabus and improving your exam scores.
CBSE Class 7 Maths Notes Chapter 8 PDF
Students can use our Class 7 Maths Chapter 8 Revision Notes if they are having trouble understanding the concepts covered in Comparing Quantities. The notes are written in a clear, concise, and accessible manner.
Students can get the Class 7 Maths Notes of Comparing Quantities from this page right now if they want to review the basics of Chapter 8 Comparing Quantities.
CBSE Class 7 Maths Notes Chapter 8 PDF
CBSE Class 7 Maths Notes Chapter 8 Comparing Quantities
Comparing Quantities:
We are often asked to compare two quantities in our day-to-day activities. These could include things like weights, grades, salaries, and heights. Two quantities must have the same units in order to be compared.
We use the ratio 150:75, or 2:1, to compare the heights of two persons who are 150 cm and 75 cm tall.
A
ratio
is a formula in mathematics that uses a particular process to compare two values.
Percentage:
A percentage is the numerator of a fraction whose denominator is 100. The sign %, which also represents a tenth, is used to represent the percentage.
Ratios to Percent:
We occasionally receive parts that need to be converted from ratios to percentages. This can easily be converted by increasing the result by 100 after dividing m by n.
It is possible to compare two ratios by converting them to like fractions. If the two fractions are equal, we say that the two provided ratios are equivalent.
If two ratios are equal, then the four quantities are said to be in proportion. For example, 8, 2, 16, and 4 are in proportion because the ratios 8:2 and 16:4 is equivalent.
A technique for comparing quantities is the percentage. A percentage is the numerator of a fraction whose denominator is 100. A hundredth of a percent is referred to as a percent. 82 percent, for instance, denotes 82 points out of a possible 100.
Decimals can be converted to percentages and vice versa, just like percentages.
For example,
0.15
=
0.15
×
100
%
=
15
%
0.15=0.15×100%=15%
.
Related Links -
For instance, we frequently use percentages in our daily lives;
-
When a percentage of the entire quantity is given, we now know how to calculate precise values.
-
When portions of a number are given to us as percentages, we've seen how to convert ratios to percentages.
-
Another way to represent an increase or decrease in a quantity is with a percentage.
-
A specific transaction's profit or loss might be expressed as a percentage.
-
The rate of interest is represented in percentages for determining loan interest. For instance, 800 was borrowed at a rate of 12 percent annually for a period of three years.
Increase or Decrease as Percent
Sometimes we need to know the percentage increase or decrease in a given quantity. Let's say the population of a state increased from 40,000 to 44,000. The population growth can then be more easily comprehended if we say that it increased by 10%.
Price related to an item or buying and selling
An item's buying price is its cost price. It goes by the shorthand CP.
The price at which you sell is known as the selling price, or SP for short.
a. If CP is less than SP, you made a profit, and it can be calculated as
SP -- CP
b. You're in a no-profit, no-loss situation if
CP = SP
c. And, the loss are equal to
CP − SP
The profit or loss might be expressed as a percentage. It is always carried out using the CP as a guide.
Simple Interest:
"Principal" denotes the amount borrowed, and "interest" is the extra money a borrower must pay for utilising borrowed funds for a predetermined duration of time (I).
The term "Time Period" (T) describes how long the money is being borrowed for. Typically, the rate of interest is stated as a percentage per year.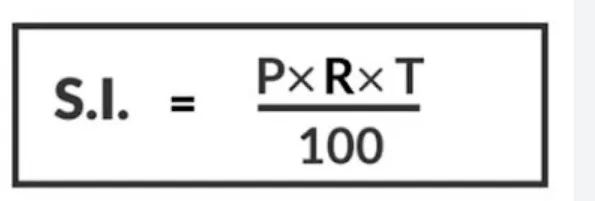
Interest for Multiple Years
If the loan amount is more than a year, interest is computed throughout the entire duration of the loan.
