
NCERT solutions for Class 9 Maths chapter 12 we have prepared NCERT Solutions for all exercise of chapter 12. Make sure to refer to the CBSE class 9 maths syllabus and go through the theory in the NCERT textbook.
These solutions complement cbse class 9 maths ncert solutions and help students practice efficiently. Physics Wallah also provides additional notes and formula summaries, making it easier to tackle exercises and exams.
NCERT Solutions for Class 9 Maths Exercise 12.1
NCERT Solutions for Class 9 Maths Exercise 12.1 guide students in applying Heron’s Formula to find areas of triangles. Step-by-step explanations simplify complex problems, helping students strengthen geometry skills and prepare for exams along with CBSE class 9 sample papers.
(Questions 1–6 content as provided)
Question 1. A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side a. Find the area of the signal board, using Heron’s formula.If its perimeter is 180 cm, what will be the area of the signal board?
Solution:
Let each side of the equilateral triangle be a.
Semi-perimeter of the triangle, 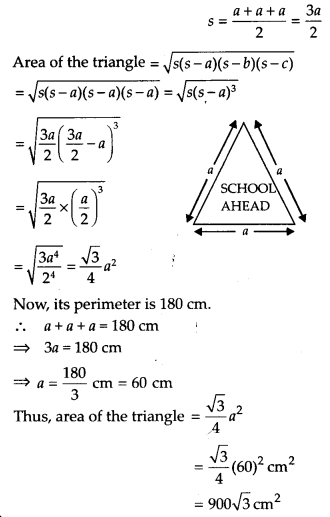
Question 2. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see figure). The advertisements yield an earning of ₹5000 per m² per year. A company hired one of its walls for 3 months. How much rent did it pay? 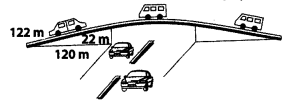
Solution:
Let the sides of the triangular will be
a = 122m, b = 12cm, c = 22m
Semi-perimeter, s = 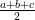
( 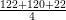 )m =
)m = 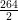 m = 132m
m = 132m
The area of the triangular side wall 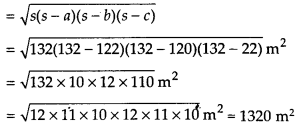
Rent for 1 year (i.e. 12 months) per m2 = Rs. 5000
∴ Rent for 3 months per m2 = Rs. 5000 x 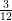
= Rent for 3 months for 1320 m2
= Rs. 5000 x 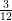 x 1320 = Rs. 16,50,000.
x 1320 = Rs. 16,50,000.
Question 3. There is a slide in a park. One of its side Company hired one of its walls for 3 months.walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see figure). If the sides of the wall are 15 m, 11 m and 6m, find the area painted in colour. 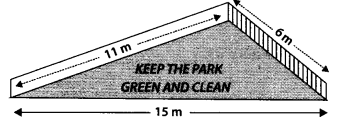
Solution:
Let the sides of the wall be
a = 15m, b = 11m, c = 6m
Semi-perimeter, 
Thus, the required area painted in colour
= 20√2 m2
Question 4. Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Solution:
Let the sides of the triangle be a
=18 cm, b = 10 cm and c = x cm
Since, perimeter of the triangle
= 42 cm
∴ 18cm + 10 cm + xcm = 42
x = [42 – (18 + 10)cm = 14cm
Now, semi-permimeter, s = 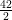 cm = 21 cm
cm = 21 cm 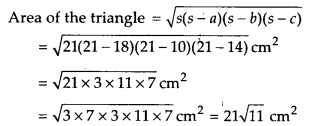
Thus, the required area of the triangle
= 21 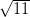 cm2
cm2
Question 5. Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area.
Solution:
Let the sides of the triangle be
a = 12x cm, b = 17x cm, c = 25x cm
Perimeter of the triangle = 540 cm
Now, 12x + 17x + 25x = 540
⇒ 54x = 54 ⇒ x = 10
∴ a = (12 x10)cm = 120cm,
b = (17 x 10) cm = 170 cm
and c = (25 x 10)cm = 250 cm
Now, semi-perimeter, s = 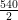 cm = 270 cm
cm = 270 cm 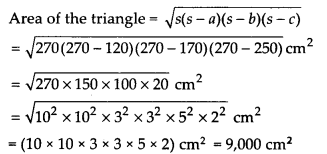
Question 6. An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Solution:
Let the sides of an isosceles triangle be
a = 12cm, b = 12cm,c = x cm
Since, perimeter of the triangle = 30 cm
∴ 12cm + 12cm + x cm = 30 cm
⇒ x = (30 – 24) = 6
Now, semi-perimeter, s = 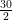 cm =15 cm
cm =15 cm 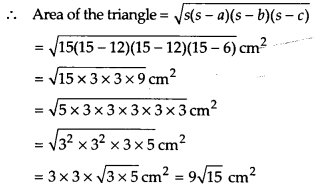
Thus, the required area of the triangle
= 9√15 cm2
NCERT Solutions for Class 9 Maths Exercise 12.2
NCERT Solutions for Class 9 Maths Exercise 12.2 help students practice advanced problems on Heron’s Formula. The detailed solutions enhance problem-solving skills and build a strong conceptual understanding, supporting preparation according to the cbse class 9 syllabus. These solutions are a vital part of cbse class 9 maths ncert solutions and exam preparation.
(Questions 1–9 content as provided)
Question 1. A park, in the shape of a quadrilateral ABCD has 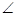 C =
C = 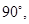 AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
Solution:
Since BD divides quadrilateral ABCD in two triangles:
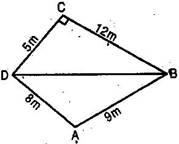
(i) Right triangle BCD and (ii)  ABD.
ABD.
In right triangle BCD, right angled at C,
therefore, Base = CD = 5 m and Altitude = BC = 12 m
 Area of
Area of  BCD =
BCD = 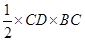 =
= 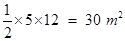
In  ABD, AB = 9 m, AD = 8 m
ABD, AB = 9 m, AD = 8 m
And BD = 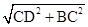 [Using Pythagoras theorem]
[Using Pythagoras theorem]
 BD =
BD = 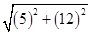 =
= 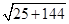 =
= 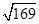 = 13 m
= 13 m
Now, Semi=perimeter of  ABD =
ABD = 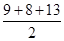 = 15 m
= 15 m
Using Heron’s formula,
Area of  ABD =
ABD = 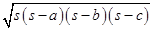
= 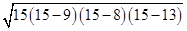 =
= 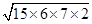
= 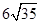 =
= 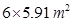
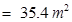 (approx.)
(approx.)
![]() Area of quadrilateral ABCD = Area of
Area of quadrilateral ABCD = Area of  BCD + Area of
BCD + Area of  ABD
ABD
= 30 + 35.4
Question 2. Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Solution:
In quadrilateral ABCE, diagonal AC divides it in two triangles,  ABC and
ABC and  ADC.
ADC.
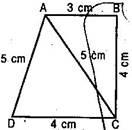
In  ABC, Semi-perimeter of
ABC, Semi-perimeter of  ABC =
ABC = 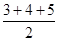 = 6 cm
= 6 cm
Using Heron’s formula,
Area of  ABC =
ABC = 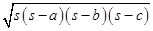
= 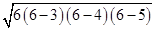 =
= 
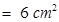
Again, In  ADC, Semi-perimeter of
ADC, Semi-perimeter of  ADC =
ADC = 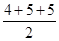 = 7 cm
= 7 cm
Using Heron’s formula, Area of  ABC =
ABC = 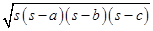
= 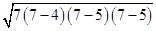 =
= 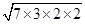 = 2
= 2 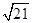
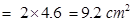 (approx.)
(approx.)
Now area of quadrilateral ABCD = Area of  ABC + Area of
ABC + Area of  ADC
ADC
= 6 + 9.2
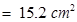
Question 3. Radha made a picture of an aeroplane with coloured paper as shown in figure. Find the total area of the paper used.
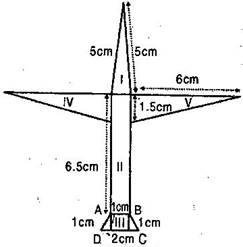
Solution:
Area of triangular part I: Here, Semi-perimeter
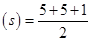 = 5.5 cm
= 5.5 cm
Therefore, Area = 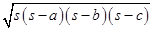
= 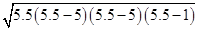
= 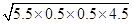 =
= 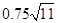
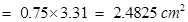
Area of triangular part II = Length x Breadth 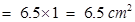
Area of triangular part III (trapezium): 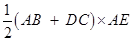
= 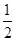 (AB + DC)
(AB + DC) 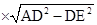 =
= 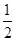 (1 + 2)
(1 + 2) 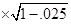
= 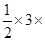
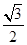 =
= 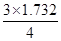
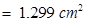
Area of triangular parts IV & V: 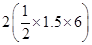
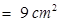
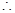 Total area = 2.4825 + 6.2 + 1.299 + 9
Total area = 2.4825 + 6.2 + 1.299 + 9 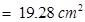
Question 4. A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 29 cm and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Solution:
Semi-perimeter of triangle 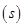 =
= 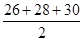 = 42 cm
= 42 cm
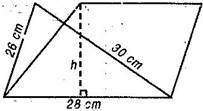
Using Heron’s formula,
Area of triangle = 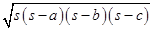
= 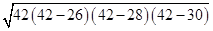
= 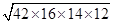
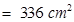
According to question, Area of parallelogram = Area of triangle
 Base x Corresponding height = 336
Base x Corresponding height = 336
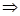
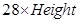 = 336
= 336
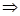 Height = 12 cm
Height = 12 cm
Question 5. A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, grass of how much area of grass field will each cow be getting?
Solution:
Here, AB = BC = CD = DA = 30 m and Diagonal AC = 48 m which divides the rhombus ABCD in two congruent triangle.
 Area of
Area of  ABC = Area of
ABC = Area of  ACD
ACD
Now, Semi-perimeter of  ABC
ABC ![]() =
= 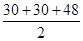 = 54 m
= 54 m
Now Area of rhombus ABCD = Area of  ABC + Area of
ABC + Area of  ACD
ACD
= 2 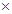 Area of
Area of  ABC [
ABC [ 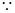 Area of
Area of  ABC = Area of
ABC = Area of  ACD]
ACD]
= 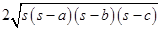 [ Using Heron’s formula]
[ Using Heron’s formula]
= 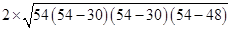
= 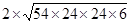 =
= 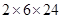
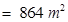
![]() Field available for 18 cows to graze the grass
Field available for 18 cows to graze the grass 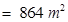
![]() Field available for 1 cow to graze the grass =
Field available for 1 cow to graze the grass = 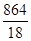
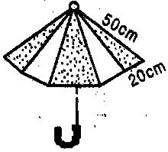
Question 6. An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?
Solution:
Here, sides of each of 10 triangular pieces of two different colours are 20 cm, 50 cm and 50 cm.
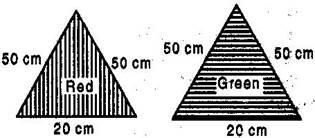
Semi-perimeter of each triangle 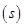 =
= 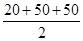 = 60 cm
= 60 cm
Now, Area of each triangle = 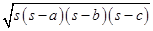
= 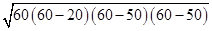
= 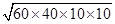 =
= 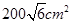
According to question, there are 5 pieces of red colour and 5 pieces of green colour.
![]() Cloth required for 5 red pieces =
Cloth required for 5 red pieces = 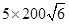 =
= 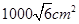
And Cloth required to 5 green pieces = 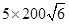 =
= 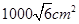
Question 7. A kite is in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and sides 6 cm each is to be made of three different shades as shown in figure.
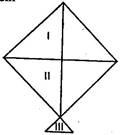
How much paper of each side has been used in it?
Solution:
Let ABCD is a square of side 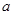 cm and diagonals AC = BD = 32 cm
cm and diagonals AC = BD = 32 cm
In right triangle ABC, 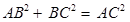 [Using Pythagoras theorem]
[Using Pythagoras theorem]
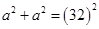
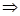
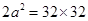
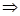
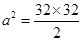 = 512
= 512
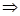 Area of square
Area of square 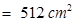 [Area of square =
[Area of square = 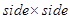 ]
]
Diagonal BD divides the square in two equal triangular parts I and II.
 Area of shaded part I = Area of shaded part II
Area of shaded part I = Area of shaded part II
= 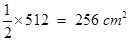
Now, semi-perimeter of shaded part III
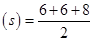 = 10 cm
= 10 cm
Area of shaded part III
= 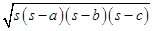
= 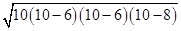
= 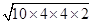 =
= 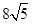
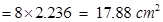
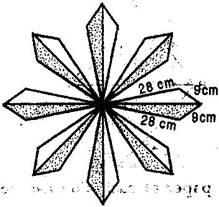
Question 8. A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see figure). Find the cost of polishing the tiles at the rate of 50 paise per cm2.
Solution:
Here, Sides of a triangular shaped tile area 9 cm, 28 cm and 35 cm.
Semi-perimeter of tile 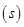 =
= 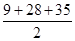 = 36 cm
= 36 cm
Area of triangular shaped tile = 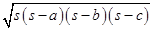
= 
= 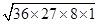 =
= 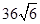
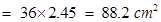 (approx.)
(approx.)
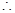 Area of 16 such tiles
Area of 16 such tiles  (Approx.)
(Approx.)
 Cost of polishing
Cost of polishing 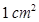 of tile = Rs. 0.50
of tile = Rs. 0.50
 Cost of polishing
Cost of polishing 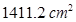 of tile
of tile
= 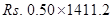 = Rs. 705.60 (Approx.)
= Rs. 705.60 (Approx.)
Question 9. A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Solution:
Let ABCD be a field in the shape of trapezium and parallel side AB = 10 m & CD = 25 m
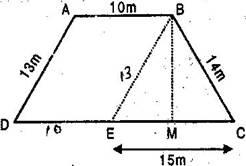
And Non-parallel sides AD = 13 m and BC = 14 m
Draw BM  DC and BE
DC and BE  AD so that ABED is a parallelogram.
AD so that ABED is a parallelogram.
 BE = AD = 13 m and DE = AB = 10 m
BE = AD = 13 m and DE = AB = 10 m
Now in  BEC, Semi-perimeter
BEC, Semi-perimeter 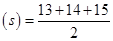
= 21 m
Area of  BEC =
BEC = 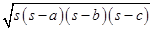
= 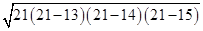
= 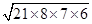 =
= 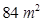
And Area of  BEC =
BEC = 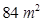
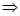
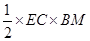 = 84
= 84
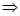
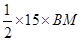 = 84
= 84
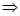 BM =
BM = 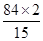 = 11.2 m
= 11.2 m
Now area of trapezium ABCD = 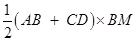
= 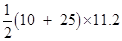
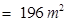
NCERT Solutions for Class 9 Maths Chapter 12 PDF
Students can download NCERT solutions for class 9 maths chapter 12 pdf to access all exercises on Heron’s Formula in one place. The PDF provides step-by-step solutions, making revision, practice, and concept strengthening easier.
It complements cbse class 9 sample papers and other cbse class 9 maths ncert solutions, serving as a convenient resource for effective exam preparation.
Do you need help with your homework or preparing for exams?
Study without using the internet
Related Chapters
NCERT Solutions for Class 9 Maths Chapter 12 Herons Formula FAQs
What are NCERT Solutions for Class 9 Maths Chapter 12 Herons Formula?
How can these solutions help in exam preparation?
Are these solutions useful for both Exercise 12.1 and 12.2?
Can I download NCERT Solutions Chapter 12 PDF?
Do these solutions include additional practice questions?
How do these solutions improve understanding of Herons Formula?









