NCERT Solutions for Class 9 Maths chapter-11 Constructions

NCERT solutions for Class 9 Maths chapter 11 Constructions is prepared by academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of chapter 11. Given below is step by step solutions of all questions given in NCERT textbook for chapter 11. Read chapter 11 theory make sure you have gone through the theory part of chapter-11 from NCERT textbook and you have learned the formula of the given chapter. Physics Wallah prepared a detail notes and additional questions for class 9 maths with short notes of all maths formula of class 9 maths. Do read these contents before moving to solve the exercise of NCERT chapter 11.

NCERT Solutions for Class 9 Maths Exercise 11.1

Question 1. Construct an angle of at the initial point of a given ray and justify the construction.

Solution:
Steps of construction:

(a) Draw a ray OA.

(b) With O as centre and convenient radius, draw an arc LM cutting OA at L.

(c) Now with L as centre and radius OL, draw an arc cutting the arc LM at P.

(d) Then taking P as centre and radius OL, draw an arc cutting arc PM at the point Q.

(e) Join OP to draw the ray OB. Also join O and Q to draw the OC. We observe that:

AOB = BOC =

(f) Now we have to bisect BOC. For this, with P as centre and radius greater than PQ draw an arc.

(g) Now with Q as centre and the same radius as in step 6, draw another arc cutting the arc drawn in step 6 at R.

(h) Join O and R and draw ray OD.

Then AOD is the required angle of

Justification:

Join PL, then OL = OP = PL [by construction]

Therefore OQP is an equilateral triangle and POL which is same as BOA is equal to

Now join QP, then OP = OQ = PQ [ by construction]

Therefore OQP is an equilateral triangle.

POQ which is same as BOC is equal to

By construction OD is bisector of BOC.

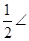DOC = DOB = BOC =

Now, DOA = BOA + DOB

DOA =

DOA =

Question 2. Construct an angle of at the initial point of a given ray and justify the construction.

Solution: 
Steps of construction:

(a) Draw a ray OA.

(b) With O as centre and convenient radius, draw an arc LM cutting OA at L.

(c) Now with L as centre and radius OL, draw an arc cutting the arc LM at P.

(d) Then taking P as centre and radius OL, draw an arc cutting arc PM at the point Q.

(e) Join OP to draw the ray OB. Also join O and Q to draw the OC. We observe that:AOB = BOC =

(f) Now we have to bisect BOC. For this, with P as centre and radius greater than PQ draw an arc.

(g) Now with Q as centre and the same radius as in step 6, draw another arc cutting the arc drawn in step 6 at R.

(h) Join O and R and draw ray OD. Then AOD is the required angle of

(i) With L as centre and radius greater than LS, draw an arc.

(j) Now with S as centre and the same radius as in step 2, draw another arc cutting the arc draw in step 2 at T.

(k) Join O and T and draw ray OE.

Thus OE bisects AOD and therefore AOE = DOE =

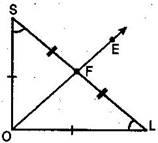
Justification:

Join LS then OLS is isosceles right triangle, right angled at O.

OL = OS

Therefore, O lies on the perpendicular bisector of SL.

SF = FL

And OFS = OFL [Each ]

Now in OFS and OFL,

OF = OF [ Common]

OS = OL [By construction]

SF = FL [Proved]

 

OFS OFL [By SSS rule]

SOF = LOF [By CPCT]

Now SOF + LOF = SOL

SOF + LOF =

2LOF =

LOF =

And AOE =

Question 3. Construct the angles of the following measurements :

(i)

(ii)

(iii)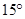

Solution: 
(i) Steps of construction:

(a) Draw a ray OA.

(b) With O as centre and a suitable radius, draw an arc LM that cuts OA at L.

(c) With L as centre and radius OL, draw an arc to cut LM at N.

(d) Join O and N draw ray OB. Then AOB =

(e) With L as centre and radius greater than LN, draw an arc.

(f) Now with N as centre and same radius as in step 5, draw another arc cutting the arc drawn in step 5 at P.

(g) Join O and P and draw ray OC. Thus OC bisects AOB and therefore AOC = BOC =

(ii) Steps of construction:

(a) Draw a ray OA.

(b) With O as centre and convenient radius, draw an arc LM cutting OA at L.

(c) Now with L as centre and radius OL, draw an arc cutting the arc LM at P.

(d) Then taking P as centre and radius OL, draw an arc cutting arc PM at the point Q.

(e) Join OP to draw the ray OB. Also join O and Q to draw the OC. We observe that:

AOB = BOC =

(f) Now we have to bisect BOC. For this, with P as centre and radius greater than PQ draw an arc.

(g) Now with Q as centre and the same radius as in step 6, draw another arc cutting the arc drawn in step 6 at R.

(h) Join O and R and draw ray OD. Then AOD is the required angle of

(i) With L as centre and radius greater than LS, draw an arc.

(j) Now with S as centre and the same radius as in step 2, draw another arc cutting the arc draw in step 2 at T.

(k) Join O and T and draw ray OE. Thus OE bisects AOD and therefore AOE = DOE = .

(l) Let ray OE intersect the arc of circle at N.

(m) Now with L as centre and radius greater than LN, draw an arc.

(n) With N as centre and same radius as in above step and draw another arc cutting arc drawn in above step at I.

(o) Join O and I and draw ray OF. Thus OF bisects AOE and therefore AOF = EOF = .

(iii) Steps of construction: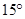

(a) Draw a ray OA.

(b) With O as centre and a suitable radius, draw an arc LM that cuts OA at L.

(c) With L as centre and radius OL, draw an arc to cut LM at N.

(d) Join O and N draw ray OB. Then AOB =

(e) With L as centre and radius greater than LN, draw an arc.

(f) Now with N as centre and same radius as in step 5, draw another arc cutting the arc drawn in step 5 at P.

(g) Join O and P and draw ray OC. Thus OC bisects AOB and therefore AOC = BOC = .

(h) Let ray OC intersects the arc of circle at point Q.

(i) Now with L as centre and radius greater than LQ; draw an arc.

(j) With Q as centre and same radius as in above step, draw another arc cutting the arc shown in above step at R.

(k) Join O and R and draw ray OS. Thus OS bisects AOC and therefore COS = AOS =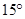

Question 4. Construct the following angles and verify by measuring them by a protractor.
(i) 75°
(ii) 105°
(iii) 135°
Solution:
Step I : Draw .
Step II : With O as centre and having a suitable radius, draw an arc which cuts at B.
Step III : With centre B and keeping the same radius, mark a point C on the previous arc.
Step IV : With centre C and having the same radius, mark another point D on the arc of step II.
Step V : Join and , which gives ∠COD = 60° = ∠BOC.
Step VI : Draw , the bisector of ∠COD, such that
∠COP = ∠COD = (60°) = 30°.
Step VII: Draw , the bisector of ∠COP, such that
∠COQ = ∠COP = (30°) = 15°.

Thus, ∠BOQ = 60° + 15° = 75°∠AOQ = 75°

(ii) Steps of Construction:
Step I : Draw .
Step II : With centre O and having a suitable radius, draw an arc which cuts at B.
Step III : With centre B and keeping the same radius, mark a point C on the previous arc.
Step IV : With centre C and having the same radius, mark another point D on the arc drawn in step II.
Step V : Draw OP, the bisector of CD which cuts CD at E such that ∠BOP = 90°.
Step VI : Draw 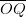, the bisector of such that ∠POQ = 15°

Thus, ∠AOQ = 90° + 15° = 105°

(iii) Steps of Construction:
Step I : Draw .
Step II : With centre O and having a suitable radius, draw an arc which cuts at A
Step III : Keeping the same radius and starting from A, mark points Q, R and S on the arc of step II such that .
StepIV :Draw , thebisector of 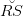which cuts the arc 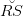at T.
Step V : Draw , the bisector of .

Thus, ∠POQ = 135°

Question 5. Construct an equilateral triangle, given its side and justify the construction.
Solution:
pt us construct an equilateral triangle, each of whose side = 3 cm(say).
Steps of Construction:
Step I : Draw .
Step II : Taking O as centre and radius equal to 3 cm, draw an arc to cut at B such that OB = 3 cm
Step III : Taking B as centre and radius equal to OB, draw an arc to intersect the previous arc at C.
Step IV : Join OC and BC.

Thus, ∆OBC is the required equilateral triangle.

Justification:
∵ The arcs 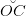and are drawn with the same radius.
∴ =
⇒ OC = BC [Chords corresponding to equal arcs are equal]
∵ OC = OB = BC
∴ OBC is an equilateral triangle.

 

NCERT Solutions for Class 9 Maths Exercise 11.2

 

Question 1. Construct a ∆ ABC in which BC = 7 cm, ∠B = 75° and AB + AC = 13 cm.
Solution:
Steps of Construction:
Step I : Draw .
Step II : Along , cut off a line segment BC = 7 cm.
Step III : At B, construct ∠CBY = 75°
Step IV : From , cut off BD = 13 cm (= AB + AC)
Step V : Join DC.
Step VI : Draw a perpendicular bisector of CD which meets BD at A.
Step VII: Join AC.

Thus, ∆ABC is the required triangle.

Question 2. Construct a ABC in which BC = 8 cm, ∠B = 45° and AB – AC = 35 cm.
Solution:
Steps of Construction:
Step I : Draw .
Step II : Along , cut off a line segment BC = 8 cm.
Step III : At B, construct ∠CBY = 45°
Step IV : From , cut off BD = 3.5 cm (= AB – AC)
Step V : Join DC.
Step VI : Draw PQ, perpendicular bisector of DC, which intersects at A.
Step VII: Join AC.

Thus, ∆ABC is the required triangle.

Question 3. Construct a ∆ ABC in which QR = 6 cm, ∠Q = 60° and PR – PQ = 2 cm.
Solution:
Steps of Construction:
Step I : Draw .
Step II : Along , cut off a line segment QR = 6 cm.
Step III : Construct a line YQY’ such that ∠RQY = 60°.
Step IV : Cut off QS = 2 cm (= PR – PQ) on QY’.
Step V : Join SR.
Step VI : Draw MN, perpendicular bisector of SR, which intersects QY at P.
Step VII: Join PR.

Thus, ∆PQR is the required triangle.

Question 4. Construct a ∆ XYZ in which ∠Y = 30°, ∠Y = 90° and XY + YZ + ZX = 11 cm.
Solution:
Steps of Construction:
Step I : Draw a line segment AB = 11 cm = (XY+YZ + ZX)
Step II : Construct ∠BAP = 30°
Step III : Construct ∠ABQ = 90°
Step IV : Draw AR, the bisector of ∠BAP.
Step V : Draw BS, the bisector of ∠ABQ. Let AR and BS intersect at X.
Step VI : Draw perpendicular bisector of , which intersects AB at Y.
Step VII: Draw perpendicular bisector of , which intersects AB at Z.
Step VIII: Join XY and XZ.

Thus, ∆XYZ is the required triangle.

Question 5. Construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm.
Solution:
Steps of Construction:
Step I : Draw BC = 12 cm.
Step II : At B, construct ∠CBY = 90°.
Step III : Along , cut off a line segment BX = 18 cm.
Step IV : Join CX.
Step V : Draw PQ, perpendicular bisector of CX, which meets BX at A.
Step VI : Join AC.

Thus, ∆ABC is the required triangle.

 

Physics Wallah team developed an additional resource material for all aspirents who are preparing for entrance exam like NEET,JEE,RMO & Olmpiads, if you are preparing for all these exam you need additional theory and questions apart from NCERT books so just click on the following chapter and get the additional theory , notes, question bank, online chapter wise test and many more ! 

 

Additional Resource and Notes for class 9 Maths

1. Probability

2. Surface Areas and Volumes

3. Coordinate Geometry

4. Pair of Linear Equations in Two Variables

5. Line and angle 

6 Number system 

7. Mensuration 

8. consutration 

9. circle 

10. Areas of parallelograms

11. Polynomial 

12. Quadrilaterial 

13. Triangle 

14. Statistics

15. euclid geometry