Rectangular Prism - Definition, Properties and Solved Examples

Rectangular Prism: We see many box-shaped things around us like bricks, books, and lunchboxes. These are all examples of a special 3D shape in maths called a rectangular prism. It is a solid shape with flat surfaces and straight edges. All its faces are in the shape of rectangles. To understand what is a rectangular prism and learn how to find the volume of a rectangular prism using simple formulas, keep reading.

Rectangular Prism

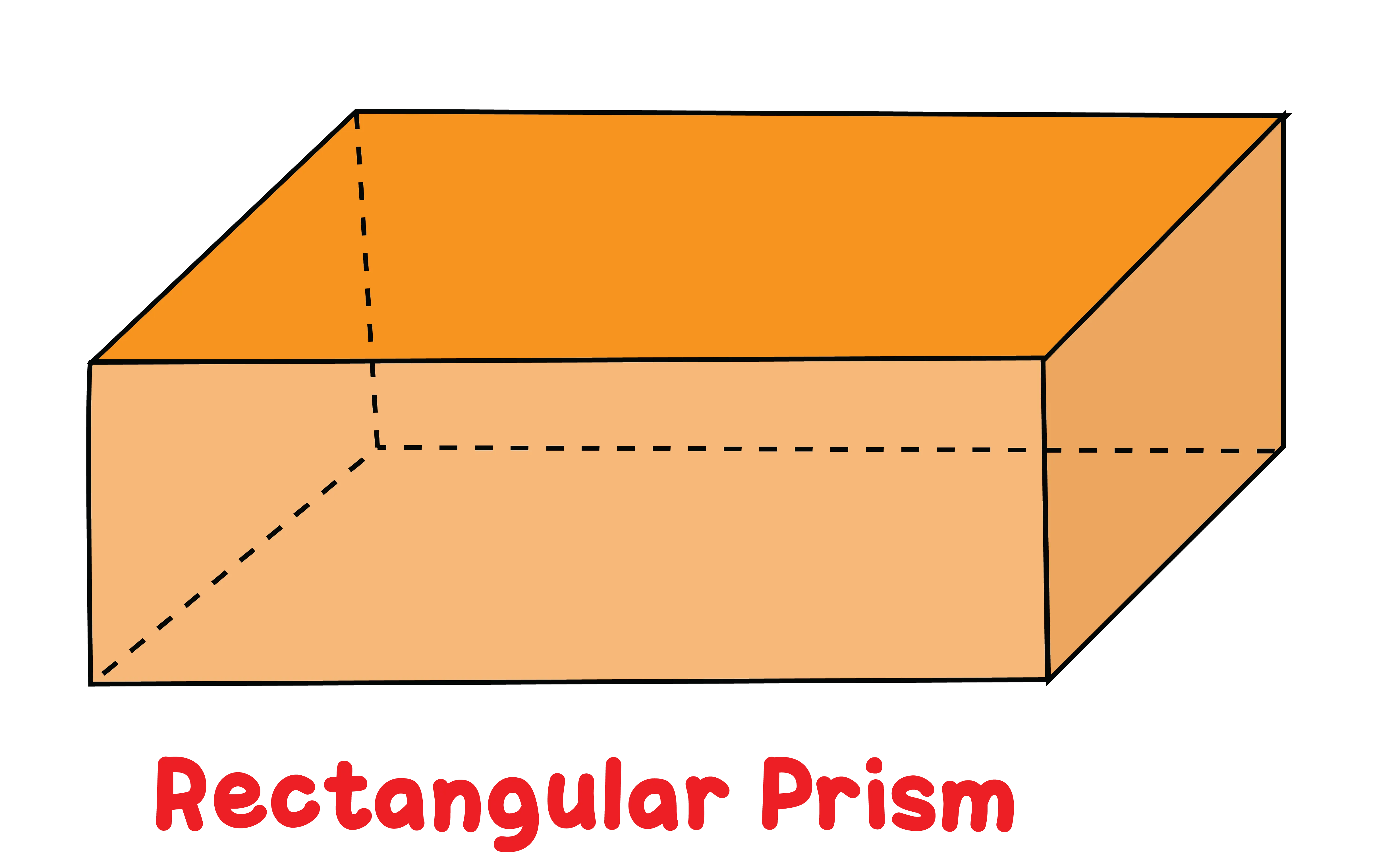
A rectangular prism is a 3D solid shape with six faces, all of which are rectangles. Think of it like a box or a brick. All its angles are right angles and opposite faces are equal. It is a common shape in everyday life.

Rectangular Prism Definition

A rectangular prism is a three-dimensional shape with six rectangular faces, and all its angles are right angles. Its sides are pairs of equal rectangles, making it a "box-like" figure. It is also called a cuboid.

What is a Rectangular Prism?- Understanding Definition

A rectangular prism is a 3D solid shape that has six flat faces, and all of them are in the shape of rectangles. It has length, width, and height, which are its three dimensions.

• The opposite faces of a rectangular prism are always the same in size.

• Because all the sides meet at right angles, it looks like a box. That’s why a rectangular prism is also known as a cuboid.

• Some everyday examples of a rectangular prism include a brick, a lunchbox, a book, or even a fish tank. This shape is part of geometry and helps students understand how space is taken up by objects in real life.

Now that students know the answer to the commonly asked question "what is a rectangular prism?" Let's learn more about its properties and types.

Read More: Unit Fraction- Definition, Examples, Practice Problems

Rectangular Prism Properties

A rectangular prism is a 3D solid shape that has the following features:

• It has 6 faces, and all of them are rectangles.

• There are 12 edges and 8 corners (vertices).

• The opposite faces are exactly the same in size and shape (congruent).

• It has three dimensions—length, width, and height.

• The top and bottom faces are called the bases, and they are always rectangular.

• In a right rectangular prism, all side faces are rectangles and meet at 90° angles.

• In an oblique rectangular prism, the side faces are parallelograms instead of rectangles.

• The cross-section of a rectangular prism is always a rectangle, no matter where we cut it straight.

Read More: What Are Mixed Numbers?

Rectangular Prism Examples

Some easy examples of rectangular prisms are a book, a brick, a matchbox, or a tissue box. You can find this shape in many objects around you at home or school. Anything shaped like a box is usually a rectangular prism.

Types of Rectangular Prism

There are two main types of rectangular prisms based on how their sides are placed:

1. Right Rectangular Prism

In the right rectangular prism, all the side faces stand straight and meet the base at right angles (90°).

• All faces are rectangles.

• The top and bottom faces (bases) are placed directly above each other.

• It looks like a regular box or cuboid.

• Most box-like things we see in daily life are examples of right rectangular prisms.

Read More: Subtraction Table

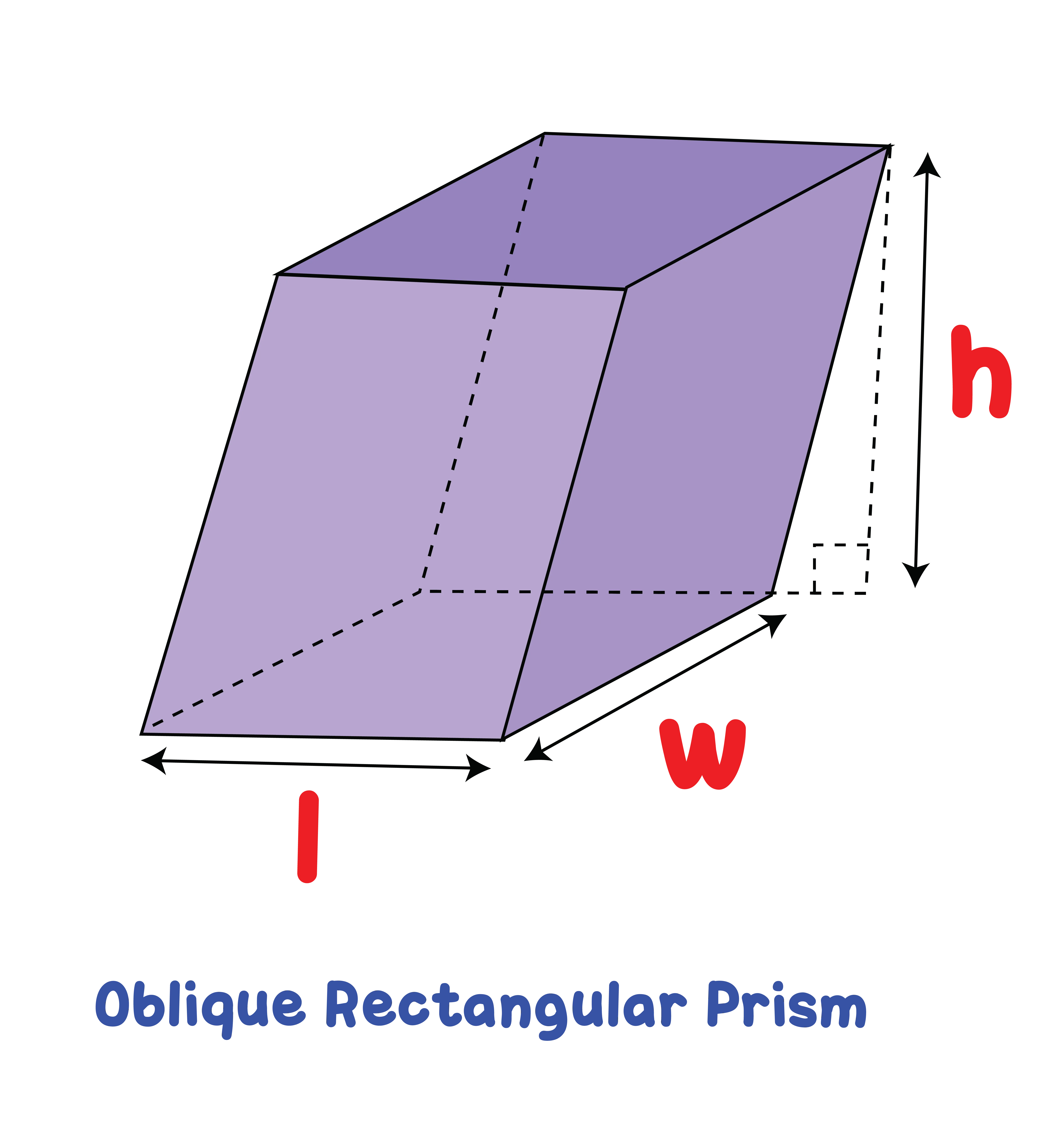
2. Oblique Rectangular Prism

In an oblique rectangular prism, the side faces lean and do not meet the base at 90°.

• The faces are not straight up; they are slanted.

• The side faces are shaped like parallelograms, not rectangles.

• The top face is not exactly above the bottom face.

Enroll Now for Kids Online Classes

Rectangular Prism Formula

As we learned above, a rectangular prism is a 3D shape, so it has both volume and surface area. To use the rectangular prism formula, it is important to know its length (l), width (w), and height (h). Let's learn in detail about both formulas of rectangular prisms one by one:

Volume of Rectangular Prism

The volume of rectangular prism represents how much space is inside the prism. The formula we use to find it is:

• Volume of Rectangular Prism = l × w × h

• The answer is given in cubic units (like cm³ or m³).

Surface Area of Rectangular Prism

The surface area is the total area of all the outer faces of the prism. A rectangular prism has two types of surface areas:

1. Lateral Surface Area (LSA): This is the total area of the four side faces, excluding the top and bottom.

• The lateral surface area can be found by this formula: LSA = 2h (l + w) square units
  where l = length, w = width, and h = height of the prism.

2. Total Surface Area (TSA): It is the sum of the areas of all six faces.

• The total surface area can be calculated using this formula: Surface Area of Rectangular Prism = 2 (lw + lh + wh)

• It is given in square units (like cm² or m²). This means adding the areas of all six rectangular faces.

This means we add the areas of all the six rectangular faces and then double it.

Hence, using the rectangular prism formula in different maths problems, students can easily find out how big a rectangular prism is and how much surface it covers.

Read More: Skip Counting Definition, Applications, and Examples

What is Rectangular Prism Net?

The definition of a rectangular prism net is that it is a flat layout that shows all the faces of the prism when it is opened and laid out on a plane. Imagine cutting along the edges of a box and spreading it flat—that is the net. It helps us see all six rectangular faces at once.

Using the rectangular prism net, students can find the total surface area of the rectangular prism by adding the areas of all these faces. Each face in the net is a rectangle with right angles, and when folded back, it forms the 3D rectangular prism shape.

Read More: A Cube Minus B Cube Formula with Examples

Solved Examples of Rectangular Prism

To understand the concept of a rectangular prism better, it is important for students to practice some questions. The solved examples of rectangular prisms given below show how to use the formulas of volume and surface area in simple math problems:

Example 1: A box has a length of 6 cm, a width of 4 cm, and a height of 3 cm. Find the volume of the box.

Solution:

Length, l = 6 cm
Width, w = 4 cm
Height, h = 3 cm

Volume of Rectangular Prism Formula = l × w × h = 6 × 4 × 3 = 72 cm³

PW CuriousJr App

Example 2: A gift box has a length of 8 cm, a width of 5 cm, and a height of 4 cm. Find the total surface area of the box.

Solution:

Length, l = 8 cm
Width, w = 5 cm
Height, h = 4 cm

Surface Area Formula of Rectangular Prism = 2 × (l × w + l × h + w × h)

Calculation:
lw = 8 × 5 = 40
lh = 8 × 4 = 32
wh = 5 × 4 = 20

Sum = 40 + 32 + 20 = 92

Surface Area of Rectangular Prism = 2 × 92 = 184 cm²

Example 3: A container has a length of 10 inches, a width of 3 inches, and a height of 7 inches. Find the volume of the container.

Solution:

Length, l = 10 in
Width, w = 3 in
Height, h = 7 in

Volume of Rectangular Prism = l × w × h = 10 × 3 × 7 = 210 in³

Example 4: A rectangular prism has a length of 12 m, a width of 6 m, and a height of 5 m. Find its surface area.

Solution:

Length, l = 12 m
Width, w = 6 m
Height, h = 5 m

Surface area formula: = 2 × (l × w + l × h + w × h)

Calculation:
lw = 12 × 6 = 72
lh = 12 × 5 = 60
wh = 6 × 5 = 30

Sum = 72 + 60 + 30 = 162

Surface Area of Rectangular Prism = 2 × 162 = 324 m²

Read More: Multiplication of Fractions

Boost Your Child’s Math Speed with CuriousJr’s Mental Maths Classes

Is your child taking too much time to answer basic math questions? The problem might not be the understanding of concepts but the calculations. Slow calculation speed in math can affect exam performance, increase stress, and lower confidence in the subject.

That’s where CuriousJr’s Mental Maths Kids Online Classes can be a real savior for your child. These classes are specially designed to solve this exact problem.

• With simple tricks and engaging methods, your child learns to think quickly and calculate faster.

• With regular sessions, they become better at solving sums faster—without relying on fingers or calculators.

• The mental maths online classes by CuriousJr are engaging, interactive, and taught in a way that builds both speed and accuracy.

Do not let slow calculation hold your child back. Book a demo class today and turn your child into a confident maths champ.