Average Rate of Change Formula: Calculation, Examples, Importance

The concept of the average rate of change involves measuring how one quantity changes in relation to another over a specific interval. This calculation provides insight into the extent of change in a function relative to a given unit of time or interval. To put it simply, the rate of change entails dividing the change in one item by the corresponding change in another item. Now, let's delve deeper into the formula for calculating the average rate of change.

What is the Average Rate of Change?

The Average Rate of Change (AROC) is a mathematical concept used to describe how a quantity changes on average with respect to another variable over a specific interval or range. It essentially measures the average amount of change in one variable divided by the corresponding change in another variable within that interval.

In simpler terms, it tells us how much something changes on average concerning another thing within a specified period or range. This concept is widely used in various fields of mathematics, science, and economics to analyze and understand how variables relate and change over time or within a given interval.

The concept of the average rate of change for a function, denoted as A(x), can be defined as the ratio of the "difference in the function's output values" to the "difference in the input values (or endpoints of the interval)." In mathematical terms, it can be calculated as [f(b) - f(a)] / (b - a), where f(b) represents the function value at point b, f(a) is the function value at point a, b is the endpoint's x-coordinate, and a is the other endpoint's x-coordinate.

Also Check – Comparing Quantities Formula

In simpler words, A(x) represents the "relationship between the change in outputs and the change in inputs," which can also be expressed as Δy / Δx, where Δy signifies the change in y-values (or function values), and Δx represents the change in x-values (or the interval's endpoints).

Here are some practical examples illustrating the concept of the average rate of change:

A bus travels at a constant speed of 80 kilometers per hour.

The number of fish in a lake increases by an average of 100 per week.

The current in an electrical circuit decreases by 0.2 amperes for every 1-volt decrease in voltage.

Also Check – Linear Equation Formula

Average Rate of Change Formula

The average rate of change function measures how one quantity changes in relation to another quantity. It's represented by the formula:

A(x) = [f(b) - f(a)] / (b - a)

Here:

A(x) stands for the average rate of change.

f(a) represents the value of function f(x) at point a.

f(b) represents the value of function f(x) at point b.

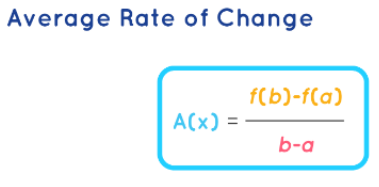
Also Check – Quadrilaterals Formula

Examples Using Average Rate of Change Formula

Certainly, here are the rephrased examples:

Example 1: Compute the average rate of change for the function f(x) = 2x + 10 as x varies from 3 to 7.

Solution:

Given:

f(x) = 2x + 10, a = 3, b = 7.

Calculate f(3):

f(3) = 2(3) + 10 = 6 + 10 = 16

Calculate f(7):

f(7) = 2(7) + 10 = 14 + 10 = 24

Using the average rate of change formula:

A(x) = [f(b) - f(a)] / (b - a)

A(x) = [f(7) - f(3)] / (7 - 3)

A(x) = (24 - 16) / 4

A(x) = 8 / 4

A(x) = 2

So, the rate of change is 2.

Example 2: Determine the average rate of change of the function f(x) = x^2 - 5x within the interval 4 ≤ x ≤ 8.

Solution:

Given:

f(x) = x ² - 5x, a = 4, b = 8.

Calculate f(4):

f(4) = (4) ² - 5(4) = 16 - 20 = -4

Calculate f(8):

f(8) = (8) ² - 5(8) = 64 - 40 = 24

Using the average rate of change formula:

A(x) = [f(b) - f(a)] / (b - a)

A(x) = (24 - (-4)) / (8 - 4)

A(x) = 28 / 4

A(x) = 7

Hence, the rate of change A(x) is 7.

Example 3: Find the rate of change for the function f(x) = 25x + 18 as x changes from 5 to 8.

Solution:

Given:

f(x) = 25x + 18, a = 5, and b = 8.

Calculate f(5):

f(5) = 25 * 5 + 18 = 125 + 18 = 143

Calculate f(8):

f(8) = 25 * 8 + 18 = 200 + 18 = 218

Using the average rate of change formula:

A(x) = [f(b) - f(a)] / (b - a)

A(x) = [218 - 143] / (8 - 5)

A(x) = 75 / 3

A(x) = 25

Therefore, the average rate of change A(x) is 25.