
Comparing Quantities Formula: In our daily lives, we frequently encounter various scenarios involving quantities, activities, and situations that require measurement and comparison. The act of comparing holds a central role in our routine. At times, we find ourselves comparing attributes such as weight, height, academic scores, speed, distance, and numerous other factors. This list of comparable quantities is extensive and diverse. However, it's important to note that only exact quantities can be directly compared; for instance, it wouldn't make sense to compare an individual's weight with another person's height. Hence, a shared reference point is essential to facilitate meaningful comparisons.
Likewise, a standardized approach is necessary when it comes to comparing quantities. Among the methods available, ratio and proportion stand out as reliable tools for this purpose. In the following discourse, we will delve into the techniques of comparing two quantities through the application of ratios and proportions. This article aims to provide a comprehensive understanding of the process of comparing diverse quantities.
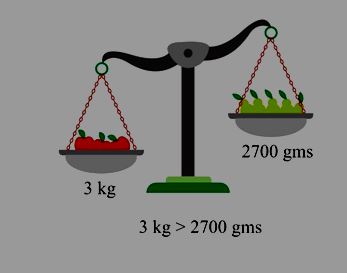
Comparing Quantities: involves the numerical connection between two amounts, showcasing the proportional magnitude of each of these amounts. Essentially, it serves as the method for evaluating and contrasting these quantities.
Also Check - coordinate geometry
Ratio
A ratio pertains to the comparison of two or more quantities that share identical units. This comparison involves dividing one quantity by another, where the number being divided is referred to as the antecedent, and the number performing the division is termed the consequent.
The mathematical symbol used to represent a ratio is ":", which is read aloud as "is to". For instance: 3:5 is articulated as "3 is to 5". In this context, "3" is denoted as the initial term or antecedent, and "5" is designated as the subsequent term or consequent. To effectively compare these two quantities, it's imperative that their units are consistent.
Also Check - Absolute Value Formula
Comparing two ratios involves the conversion of both ratios into equivalent fractions with matching denominators. If these fractions are identical, it indicates that the original ratios are equivalent or proportionate. For instance: 6cm:3m can be transformed as follows:
6cm:3m = 6cm:300cm
⇒ 6cm/6cm : 300cm/6cm
⇒ 1:50
Thus, 6cm:3m is equivalent to the ratio 1:50. Consequently, it can be concluded that the ratios 6cm:3m and 1:50 are indicative of the same relative proportions.
Also Check - Algebra Formulas
Ratio Formula
Let's imagine that we have a pair of quantities (or numbers or entities) that require a ratio to be determined between them. In such a scenario, the formula for calculating the ratio is as follows:
m:n = m/n
In this context, both "m" and "n" can represent any two given quantities.
Within this framework, "m" is identified as the initial term or antecedent, while "n" is recognized as the subsequent term or consequent.
For instance, consider the ratio 6:11, which can be expressed as 6/11. Here, 6 represents the antecedent and 11 stands as the consequent.
A noteworthy principle is that if each term of a ratio is both multiplied and divided by the same non-zero number, the ratio's fundamental value remains unaltered.
To illustrate this point, take the example: 6:11 = 12:22 = 18:33. This showcases that modifying the terms of the ratio using this method does not affect its underlying ratio relationship.
Proportion
Proportion represents an equation that establishes the equivalence of two provided ratios. Put differently, a proportion signifies the equality between two fractions or ratios. When two ratios possess an identical numerical value, they are categorized as being proportional. Consequently, if two ratios are synonymous (or equal), it follows that the four quantities involved maintain a state of proportionality.
Essentially, a proportion is a clear assertion of the equality between two ratios. This assertion can be represented in either of the following forms:
- a:b=c:d
- a:b::c:d
For instance, let's explore the question of whether the numbers 15, 20, 45, and 60 are in proportion:
The given ratios can be expressed as 15:20::45:60.
The ratio of 15 to 20 equals 15/20, which simplifies to 3/4, represented as 3:4.
Similarly, the ratio of 45 to 60 equals 45/60, which also simplifies to 3/4.
Because 15:20 is equivalent to 45:60, it can be deduced that the provided numbers, 15, 20, 45, and 60, are indeed in proportion.
Proportion Formula
Let's consider a scenario where we have two ratios, denoted as p:q and r:s, that are in proportion. In this context, the terms 'q' and 'r' are referred to as the 'means' or 'mean terms,' while the terms 'p' and 's' are identified as the 'extremes' or 'extreme terms.'
This relationship between the ratios can be expressed as follows:
- pq = rs
or
- p:q::r:s
This equation can be further interpreted as:
"The product of the extremes is equal to the product of the means."
Mathematically, this translates to:
"first term × fourth term = second term × third term"
which simplifies to:
pr = qs
For instance, let's explore the question of whether the numbers 60, 80, 90, and 120 are in proportion:
The given values can be written as 60:80::90:120.
The ratio of 30 to 40 equals 30/40, which simplifies to 3/4, represented as 3:4.
Similarly, the ratio of 45 to 60 also equals 3/4.
Since 30:40 is equivalent to 45:60, it can be concluded that the provided numbers, 60, 80, 90, and 120, are indeed in proportion.
Also Check - Linear Equation Formula
Percentage
This represents an alternative approach to comparing quantities, signifying a relation to each hundred units. In fractional representation, where the denominator is 100, the numerator denotes the percentage and is symbolized by the special sign %, which reads as "percent."
There are two techniques for determining percentages:
- Fraction Method
Illustration:
Consider a scenario where there are 20 boys among 50 students in a class. The objective is to ascertain the percentage of boys.
To standardize the denominator as one hundred, both the numerator and the denominator need to be multiplied by 2.
This yields a percentage of 40% for boys.
- Unitary Method
In the unitary method, the initial step involves determining the value of a single unit, followed by its multiplication with the desired number of units.
Illustration:
Referring to the earlier example with 20 boys among 50 students, if we wish to determine the number of boys among 100 students:
Given that 20 boys represent one unit in a group of 50 students, we can conclude that among 100 students, the number of boys would be equivalent to:
It's important to note that the unitary method allows for direct calculations of proportions based on the unit value.
Prices Related to Buying and Selling (Profit and Loss)
Terms Related to Buying and Selling
Cost Price (CP)
The cost price is the actual amount that is paid by the manufacturer to produce it or to provide the service.
Selling Price (SP)
It is the amount at which the product is sold in the market by the retailer.
Profit
After selling a product if the seller has some financial gains then it is said to be a profit.
Profit = SP – CP

Loss
It is the financial negative revenue that a seller has to bear while selling the product.
Loss = CP – SP
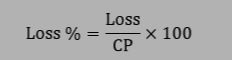
Sales Tax/Value Added Tax/Goods and Services Tax
The amount charged by the government on the sale of an item is called Sales Tax . The shopkeeper collects it from the customer and gives it to the government. So the sales tax will always be on the selling price of the item and is added to the value of the bill.
Earlier you must have seen Sales tax on the bill, nowadays; you will mostly see Value Added Tax
Formula
If the tax is x%, then the Total price after including tax would be
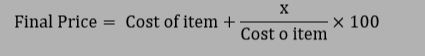
Compounded Interest
Interest is the extra money paid by the banks on our money at a fixed rate of interest.
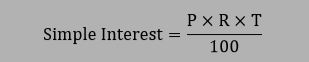
Where P = Principal amount
R = Rate of interest
T = Time period for which the interest is paid
The interest calculated both on the principal and the interest earned is called compounded interest
The Formula for Compound Interest
As the above method is very long and it cannot be used at every place so we can use the formula to find the compound interest.
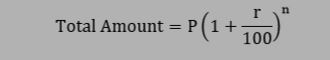
Compound Interest (CI) = Amount (A) – Principal (P)
Important Formulas Related to Comparing Quantities
Here are some formulas that will aid students in grasping fundamental arithmetic concepts related to money:
- Profit = Selling price – Cost price
- Loss = Cost price – Selling price
- If Selling Price (SP) > Cost Price (CP), then it's a profit.
- If SP = CP, then it's neither profit nor loss.
- If CP > SP, then it's a loss.
- Discount = Marked Price – Sale Price
- Discount Percentage = (Discount × 100) / Marked Price
- Profit Percentage = (Profit / Cost Price) × 100
- Loss Percentage = (Loss / Cost Price) × 100
- Percentage Increased = Change in Value / Original Value
- Simple Interest = (Principal × Rate × Time) / 100
- Compound Interest Formula = Amount – Principal
- Sales Tax or VAT = Tax on Selling Price = (Cost Price × Rate of Sales Tax) / 100
- Billing Amount = Selling price + VAT
Comparing Quantities Examples
Comparing Quantities Formula FAQs
Define the term comparing quantities.
Explain the term equivalent ratio.
If two ratios are equivalent, then the four quantities are said to be in ______.
To convert a fraction into a percent, we _________ it by 100.










