
Refractive Index Formula: The Refractive Index characterizes a material's property that establishes the relationship between the speed of light in the material and its speed in a vacuum. Represented by the symbol μ, it signifies the extent to which light particles are absorbed and re-emitted by a medium, consequently reducing the speed of light when traveling through it instead of a vacuum.
Light Refraction
When light rays travel obliquely from one medium to another, an observable change in the path or direction of light propagation occurs. This phenomenon is commonly referred to as the refraction of light. In simple terms, it describes the change in the speed or velocity of light as it transitions from one medium to another. The extent of light refraction is influenced by the velocity of the material medium and the characteristics of the medium through which the light originates. This refraction phenomenon adheres to specific laws that follow the observed changes in the speed of light rays.
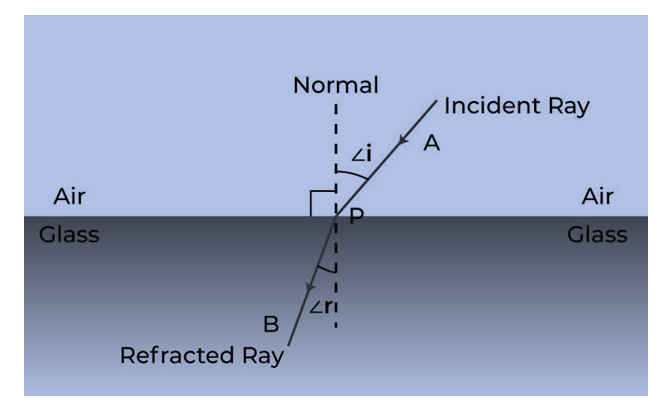
The illustration above depicts refraction through two distinct media. The light ray undergoes a change in its trajectory as it transitions from air to glass, and a similar alteration will occur when the reverse process takes place.
Refractive Index Formula Laws of Refraction
Two fundamental laws follow the phenomenon of refraction, shaping the behavior of light during this process and influencing the formation of the refracted image: The refracted ray, the incident (or obliquely falling) ray, and the normal ray at the point of incidence all lie in the same plane. Snell's Law states that the ratio of the sine of the angle of incidence (i) to the sine of the angle of refraction (r) is constant:
Sinr / sini =constant
Where:
i is the angle of incidence
r is the angle of refraction.
The constant value depends upon the refractive indexes of the two mediums involved, representing their ratio and possessing dimensionless characteristics.
What is the Refractive Index Formula
To begin with, the refractive index is a dimensionless quantity. It is a measure, expressed as the index of refraction or simply refractive index, that informs us about the speed of light as it moves through a material medium. This index provides insight into the speed of light when traversing diverse mediums. When light changes its direction while moving obliquely from one medium to another, the degree of alteration in the direction of light rays is referred to and calculated as the refractive index. The refractive index is determined by the ratio of the velocities or speeds of light in different media.
There are two types of refractive index Formula:
- Absolute Refractive Index Formula
- Relative Refractive Index Formula
The category of refractive index is determined by the two mediums through which light travels. The absolute refractive index involves one material medium and one vacuum, with the speed of light set at 3 × 10^8 m/s. On the other hand, the relative refractive index signifies the proportional change in the speed or velocity of light when transitioning from one specified medium to another.
When light travels from a rarer medium to a denser one, the light rays incline toward the normal. Conversely, if the light travels from a denser medium to a rarer one, it bends away from the normal at the point of incidence.
Absolute Refractive Index Formula
In the context of a given material medium, the refractive index is defined as the ratio of the speed or velocity of light in a vacuum (c) to the speed of light in the specific material medium (v) through which it travels. The refractive index, denoted by the symbol n, is expressed by the following formula:
Refractive Index Formula n v = c / v
where: c is the velocity of light in a vacuum, v is the velocity of light in the provided medium. The velocity of light in a vacuum is 3 × 10^8 m/s. In air, the speed is nearly the same as in a vacuum, with a minimal difference.
Therefore, when light travels from air to a medium, the speed is considered to be 3 × 10^8 m/s. The absolute refractive index, as implied by its name, provides a rough estimate of the optical density of the given material. The table offers an overview of the absolute refractive indices of various mediums.
A substance with a higher refractive index is optically denser compared to a material with a lower refractive index, which is considered a rarer medium. It's important to note that a higher optical density does not necessarily indicate a higher mass per unit volume density, as these are distinct properties. For example, kerosene has a lower density than water, but it is optically denser, as evidenced by its higher refractive index of 1.44 compared to water's refractive index of 1.33.
Relative Refractive Index Formula
Relative Refractive Index The relative refractive index pertains to the refractive index of one material medium in relation to another. The relative refractive index can be determined by the velocities of light in different media using the following formulas, where the first medium is not a vacuum:
Refractive Index Formula n 21 = v 1 / v 2
where: n 21 is the refractive index of the speed of light in material medium 2 with respect to the velocity of light in medium 1. Similarly,
Refractive Index Formula n 12 = v 2 / v 1
where: n 12 is the refractive index of the speed of light in material medium 1 with respect to the velocity of light in medium 2.When light travels from a rarer to a denser medium, it bends toward the normal, and conversely, when it travels from a denser to a rarer medium, it bends away from the normal. This phenomenon can be observed in the case of ice and kerosene, where the refractive index of ice is lower than that of kerosene. Consequently, the light ray, upon traveling from ice to kerosene, bends toward the normal. The ratio of their refractive indices provides us with the relative refractive index.
Refractive Index Formula Optical Density
Optical Density An optically denser medium is characterized by having a higher refractive index compared to vacuum. In such a medium, the speed of light is slower when compared to an optically rarer medium. Calculation of Refractive Index from the Speed of Light The refractive index ( n) can be easily determined when the speed of light is known in two different mediums.
Using the symbols v 1 and v 2 to represent the speeds of light in the first and second mediums, respectively, the refractive index ( n 21 ) of the second medium with respect to the first is given by:
Refractive Index Formula n 21 = v 1 / v 2
Similarly, the refractive index ( n 12 ) of the first medium with respect to the second is given by:
Refractive Index Formula n 12 = v 2 / v 1
Why is a High Refractive Index Important for Optical Polymers?
A high refractive index is crucial for optical polymers because it facilitates a greater bending of light rays within the material, leading to a reduction in the profile of the lens. By increasing the refractive index, the thickness of the lens decreases, resulting in a lighter weight for the optical polymer.
What is Refractive Index Gradient?
Refractive Index Gradient represents the rate of change of the refractive index concerning the distance traveled within the optical material. It is expressed as the reciprocal of a unit of distance and is a vector point function.
How Does the Refractive Index Vary with Wavelength?
The refractive index of a material varies with the wavelength of light. This is because the speed of light is the product of frequency and wavelength. Although the frequency of the light wave remains constant regardless of the medium it traverses, the velocity of light changes with the medium. To compensate for this change in velocity, the wavelength of the light wave also changes based on refraction.
Applications of Refractive Index
The article outlines various practical applications of refractive index:
- Refractive index is extensively used for identifying specific substances, confirming their purity, and measuring concentrations.
- Refractive index is applied in the pharmaceutical industry to determine drug concentrations, aiding in quality control and formulation processes.
- Refractive index finds application in estimating the thermophysical properties of various hydrocarbons and petroleum mixtures, providing valuable information in industries related to these substances.
- Widely used to calculate the focusing power of lenses and the dispersive power of prisms, contributing to the design and optimization of optical systems.
- Commonly, it is utilized for measuring the concentration of solutes in aqueous solutions. For example, in a sugar solution, the refractive index can be used to determine the sugar content.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Physics knowledge. and build a strong foundation.
| Related Links | |
| Equivalent Resistance Formula | Uniform Circular Motion Formula |
| Dynamic Viscosity Formula | Tangential Acceleration Formula |
Refractive Index Formula FAQs
What is the refractive index formula?
How is the absolute refractive index determined?
What is the relative refractive index formula?
Why is a high refractive index important in optical polymers?










