
Equivalent Resistance Formula: Equivalent resistance is the aggregate resistance within a circuit when resistors are linked in either series or parallel configurations. Resistors, which are electrical components that flow current in a circuit according to Ohm's law (V = IR), may be multiple within a circuit. Consequently, the determination of equivalent resistance is dependent on the arrangement of resistors in the circuit, influencing the current and voltage values.
What is Equivalent Resistance Formula
Equivalent Resistance refers to the overall resistance resulting from the combination of all resistances within a circuit. If n resistances are added to the circuit, either in series or parallel, and if we substitute all these resistances with a single resistance in a manner that the current and voltage difference in the circuit remain unchanged, it is termed as equivalent resistance.
The symbol for Equivalent Resistance is Req. The SI unit for the measurement of Equivalent Resistance is Ohm (Ω), and its dimensional formula is [M 1 L 2 A −2 T −3 ].Equivalent Resistance Formula
The calculation of Equivalent Resistance involves specific formulas for series and parallel combinations. There are distinct equivalent resistance formulas for each configuration:
- Equivalent Resistance Formula for Series Combination.
- Equivalent Resistance Formula for Parallel Combination.
Equivalent Resistance Formula for Series Combination
In a series circuit containing n resistors (where n > 1), the resistors are interconnected consecutively, allowing the entire set to be substituted by a single equivalent resistor with an identical resistance value. In this configuration, the equivalent resistance is the sum of the individual resistances. While the current remains constant across each resistor, the voltage is distributed into n segments among the resistors.

The formula for equivalent resistance (R eq ) in a series combination is given by:
R eq =R 1 +R 2 +R 3 +…+R n
Req represents the equivalent resistance, R 1 signifies the resistance of the initial resistor, R 2 denotes the resistance of the second resistor, R 3 indicates the resistance of the third resistor, and R n represents the resistance of the nth resistor.
Equivalent Resistance Formula for Parallel Combination
In a parallel circuit comprising n resistors (where n > 1), the resistors are connected in parallel through wires originating from a common point. In this configuration, the reciprocal of the equivalent resistance is equivalent to the sum of the reciprocals of individual resistances. While the voltage across each resistor remains constant, the current is distributed into n segments among the resistors.
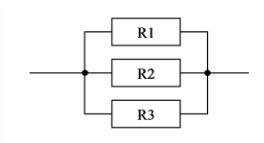
The formula for equivalent resistance (R eq ) in a parallel combination is expressed as:
1 /R eq = 1/R 1 + 1/R 2 + 1/R 3 ...+ 1/R n
Req represents the equivalent resistance, R 1 signifies the resistance of the initial resistor, R 2 denotes the resistance of the second resistor, R 3 indicates the resistance of the third resistor, and R n represents the resistance of the nth resistor.
Equivalent Resistance Formula Solved Examples
Example 1: Question: What is the equivalent resistance if three resistances of 4 Ω, 2 Ω, and 5 Ω are connected in series?
Solution: Given resistances in series: R 1 =7Ω, R 2 =2Ω, R 3 =5Ω.
Using the formula
R eq =R 1 +R 2 +R 3
R eq =7Ω+2Ω+5Ω=14Ω
Example 2: Find the unknown resistance if three resistances of 2 Ω, 5 Ω, and x Ω are connected in series to give an equivalent resistance of 10 Ω.
Solution: Given resistances in series: R 1 =2Ω, R 2 =4Ω.
Given equivalent resistance:
R eq =R 1 +R 2 +R 3
10Ω=2Ω+4Ω+xΩ
10 Ω =6Ω+xΩ
x=4Ω
Example 3 : Question: What is the equivalent resistance if three resistances of 6 Ω, 3 Ω, and 8 Ω are connected in parallel?
Solution: Given resistances in parallel: R 1 =6Ω, R 2 =3Ω, R 3 =8Ω. Using the formula
1 /R eq = 1/R 1 + 1/R 2 +1/ R 3
1/R eq = 1/6 + 1/3 + 1/8
1/ R eq = 4+8+3 / 24
1/ R eq = 15 /24
R eq = 24/15 Ω
R eq =1.6Ω.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Physics knowledge. and build a strong foundation.
| Related Links | |
| Mechanical Advantage Formula | Brownian Motion Formula |
| Intensity Formula | Tangential Acceleration Formula |
Equivalent Resistance Formula FAQs
What is Equivalent Resistance?
What is the formula for Equivalent Resistance in a Series Circuit?
What is the formula for Equivalent Resistance in a Parallel Circuit?
How is Equivalent Resistance Calculated in a Series Circuit?










