
A polynomial Formula is a mathematical expression consisting of variables (also known as indeterminates) and coefficients, combined using addition, subtraction, and multiplication operations. The expression typically involves non-negative integer exponents on the variables. Polynomials can have one or more terms, where each term comprises, a coefficient multiplied by a variable raised to a specific exponent. The terms are then combined through addition or subtraction to form the overall polynomial expression. The degree of a polynomial is determined by the highest exponent present in the expression. Polynomials are a foundational concept in algebra and have a wide range of applications in various mathematical and scientific fields.
Also Check - Rational Number FormulaDefine the Polynomial Formula
A polynomial formula encapsulates the representation of a polynomial expression. A polynomial expression entails two or more algebraic terms, with the formation of such expressions involving repeated addition or subtraction of binomials or monomials. This process gives rise to polynomials containing both similar and dissimilar terms. Similar terms within polynomials possess matching variables and exponents, while distinct terms encompass varying variables and powers.
The polynomial formula consists of variables raised to different powers, and the highest power of the variable upon evaluation determines the polynomial's degree. The polynomial formula is also recognized as the standard representation of the polynomial, wherein the variables are organized in descending order of their exponents within the formula.
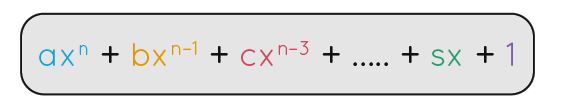
Polynomial formula is represented as below
(ax n +bx {n−1}+ cx {n−3} +……+rx+s)
- a, b, c, ..., s are coefficients
- x is the variable
- n is the degree of the polynomial
Basic formulas related to the polynomial expression are,
1.F(x) = a n (x n )
where
- a is the coefficient
- x is the variable
- n is the exponent
- F(x) = a n x n + a n-1 x n-1 + a n-2 x n-2 + …….. + a 1 x +a 0 = 0
- F(x)=a n x n +..+rx+s
- n is a natural number
a n −b n =(a−b)(a n −1+a n −2b+…)
- n is an even number
a n +b n =(a+b)(a n −1−a n −2b+…)
- n is an odd number
- a n +b n =(a+b)(a n −1−a n −2b+…)
What is a Polynomial Equation?
A polynomial equation emerges when a polynomial expression is set to be equivalent to zero. In essence, it's a mathematical equation that involves variables, coefficients, non-negative integer exponents, arithmetic operations, and an equality sign. Within the equation, there exist, distinct exponents, with the highest exponent determining the equation's degree. A prerequisite for an equation to be classified as a polynomial equation is that the involved variables can possess solely non-negative integer exponents. This means that the exponents associated with the variables must strictly avoid being negative or fractional.
Illustratively, consider the polynomial 2x^2 + 3x + 1; it fits the criteria of a polynomial, thus rendering the equation 2x^2 + 3x + 1 = 0 a polynomial equation.
Below, you'll find additional instances of polynomial equations:

Polynomial Equation Formula
A polynomial equation invariably takes the structure "polynomial = 0". In algebraic terms, it is represented as p(x) = a n x n + a n - 1 x n - 1 + ... + a 1 x + a0 = 0, , where:
- a n , a n - 1, ...., a 1 , a 0 represent coefficients, all being real numbers.
- 'x' denotes the variable.
- p(x) signifies the polynomial with respect to the variable x.
- 'n' stands as a non-negative integer, serving as the highest exponent which defines the degree of p(x).
Polynomial Equation Examples
| Equation | Polynomial Equation or Not | Reason |
|---|---|---|
| x 2 + 3√x + 1 = 0 | No | √x = x 1/2 and 1/2 is a non-integer value. |
| x 2 + √3 x + 1 = 0 | Yes | The exponents of x are all whole numbers (constants can still be non-whole numbers). |
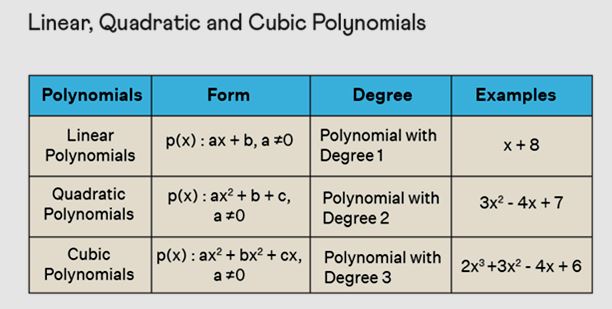
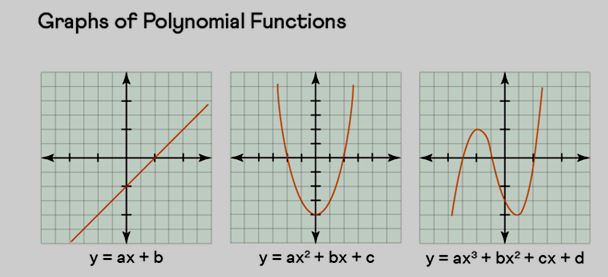
Types of Polynomial Equations
The classification of a polynomial equation is determined by its degree, which corresponds to the greatest exponent of the variable. Primarily, there exist four categories of polynomial equations:
- Linear Polynomial Equation.
- Quadratic Polynomial Equation.
- Cubic Polynomial Equation.
- Biquadratic Polynomial Equation.
Polynomial equations that do not fit within these categories are referred to as higher-degree polynomial equations.
Linear Equations
These constitute polynomial equations of degree 1. They take the form ax + b = 0.
Instances include 2x + 3 = 0, 5x - 7 = 0, and similar cases.
Quadratic Equations
These represent polynomial equations of degree 2. They are structured as ax 2 + bx + c = 0.
Illustrations include: 3x 2 - 5x + 7 = 0, x 2 + 6x + 7 = 0 , among others.
Download PDF Polynomial Formula
Cubic Equations
These constitute polynomial equations of degree 4. They follow the format ax 4 + bx 3 + cx 2 + dx + e = 0.
For example: 3x 4 - 5x + 2 = 0.
Solving Polynomial Equations
The procedure of solving a polynomial equation p(x) = 0 entails determining the value(s) of 'x' that fulfill the equation. A numeric value 'a' is defined as a 'zero' of a polynomial p(x) only if p(a) = 0. In this context, 'a' is also referred to as a root of the polynomial equation p(x) = 0. Consequently, the process of solving polynomial equations essentially revolves around identifying their roots.
In the case of solving polynomials beyond these categories, techniques such as the remainder theorem, factor theorem, rational root theorem, and synthetic division offer valuable assistance.
Also Check - Coordinate Geometry FormulaDifference Between Polynomial and Equation
A polynomial serves as the overarching term encompassing a specific category of algebraic expressions, which incorporate variables, constants, and employ operations like addition, subtraction, multiplication, and division, while exclusively utilizing non-negative exponents for the variables.
Illustration: 2x + 3
A polynomial equation, on the other hand, constitutes a mathematical statement featuring an 'equal to' sign between two algebraic expressions that hold equal values.
Illustration: 2x + 3 = 7
Applications of Polynomial Formula
Its utility extends across various domains such as engineering, computer science, management, business, and agriculture. This mathematical concept facilitates the creation of expressions that define known and unknown quantities using variables and constants.
Polynomial equations are constructed by incorporating variables, exponents, and coefficients. Solving polynomials entails factoring them based on their degree or the variables featured within the provided equation.
Points to remember
- The polynomial equation's degree corresponds to the greatest exponent of the variable present in the equation.
- Solving an equation involves identifying the values of the variables that make the equation valid.
- Furthermore, it's possible to deduce a polynomial equation when the roots are given.
Polynomials Formula FAQs
What distinguishes a Polynomial from a Polynomial Equation?
What does the formula for a Polynomial Equation look like?
What doesn't qualify as a Polynomial Equation?
How can you determine the degree of Polynomial Equations?










