
NCERT Solutions for Class 6 Maths Chapter 14
NCERT Solutions For Class 6 Maths Chapter 14: NCERT Solutions For Class 6 Maths Chapter 14, Practical Geometry, includes solved questions for each exercise related to Practical Geometry. The PDF is easily downloadable, allowing learning at any place and time. To understand the question types and effective problem-solving methods in Practical Geometry, students should refer to NCERT Solutions for Class 6 Maths Chapter 14 without skipping. These solutions, designed for easy comprehension, are created by experienced subject experts with years of teaching experience. Any doubts regarding Class 6 Maths Chapter 14 can be clarified by reaching out to our experts. Utilizing NCERT Solutions for Class 6 Maths Chapter 14 in your exam preparation will be beneficial. Access to NCERT Solutions for Class 6 Science, Maths, English, Hindi, and other subjects can simplify the study of these subjects.
NCERT Solutions for Class 6 Maths Chapter 14 PDF Download
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry
PhysicsWallah offers trustworthy answers for NCERT Class 6 Maths chapter 14. The solutions for NCERT chapter 14 practical geometry class 6 are created by our subject specialists in a step-by-step approach. You can easily get the NCERT Solution for Class 6 Maths chapter 14 practical geometry in to study offline whenever you want. Exercise 14.1 Page No: 276 1. Draw a circle of radius 3.2 cm. Solutions: The required circle may be drawn as follows: Step 1: For the required radius 3.2 cm, first open the compasses. Step 2: For the centre of a circle, mark a point ‘O’. Step 3: Place a pointer of compasses on ‘O’. Step 4: Now, turn the compasses slowly to draw the required circle.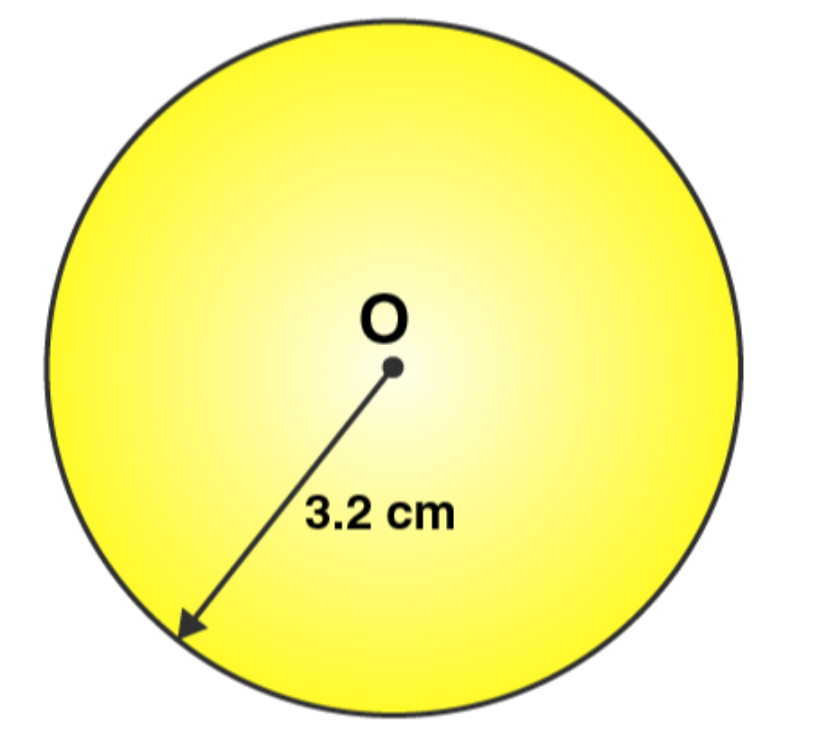 2. With the same centre O, draw two circles of radii 4 cm and 2.5 cm.
Solutions:
The required circle may be drawn as follows:
Step 1: For the required radius 4 cm, first open the compasses
Step 2: For the centre of a circle, mark a point ‘O’
Step 3: Place a pointer of compasses on ‘O’.
Step 4: Turn the compasses slowly to draw the circle.
Step 5: Next, open the compasses for 2.5 cm.
Step 6: Again place a pointer of compasses on ‘O’ and turn the compasses slowly to draw the circle.
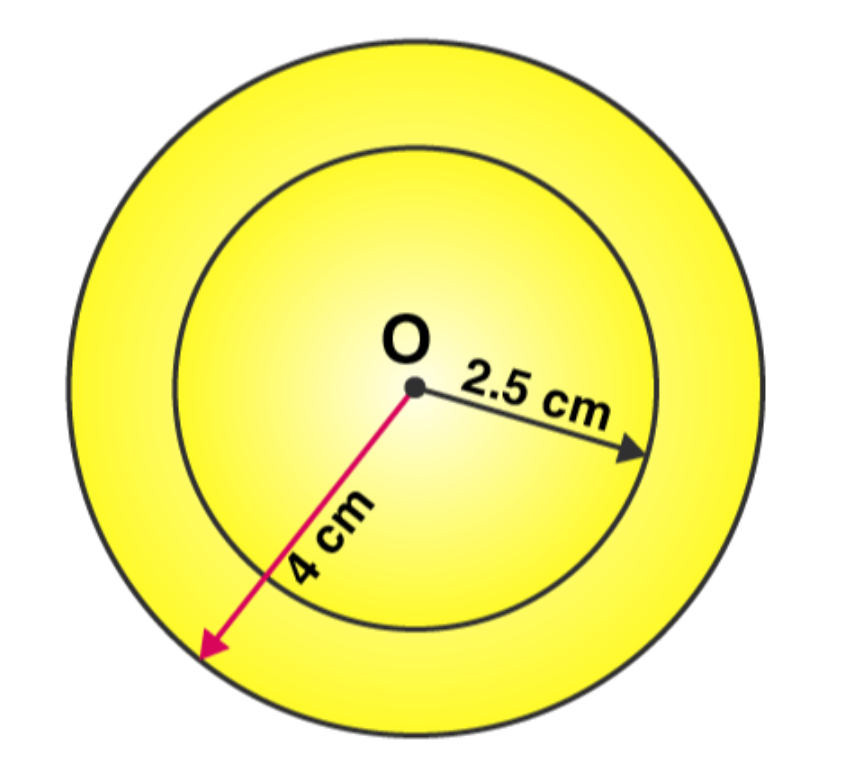
2. With the same centre O, draw two circles of radii 4 cm and 2.5 cm.
Solutions:
The required circle may be drawn as follows:
Step 1: For the required radius 4 cm, first open the compasses
Step 2: For the centre of a circle, mark a point ‘O’
Step 3: Place a pointer of compasses on ‘O’.
Step 4: Turn the compasses slowly to draw the circle.
Step 5: Next, open the compasses for 2.5 cm.
Step 6: Again place a pointer of compasses on ‘O’ and turn the compasses slowly to draw the circle.
 3. Draw a circle and any two of its diameters. If you join the ends of these diameters, what is the figure obtained? What figure is obtained if the diameters are perpendicular to each other? How do you check your answer?
Solutions:
We may draw a circle having its centre ‘O’, also of any convenient radius. Let AB and CD be the two diameters of this circle. A quadrilateral is formed when we join the ends of these diameters.
3. Draw a circle and any two of its diameters. If you join the ends of these diameters, what is the figure obtained? What figure is obtained if the diameters are perpendicular to each other? How do you check your answer?
Solutions:
We may draw a circle having its centre ‘O’, also of any convenient radius. Let AB and CD be the two diameters of this circle. A quadrilateral is formed when we join the ends of these diameters.
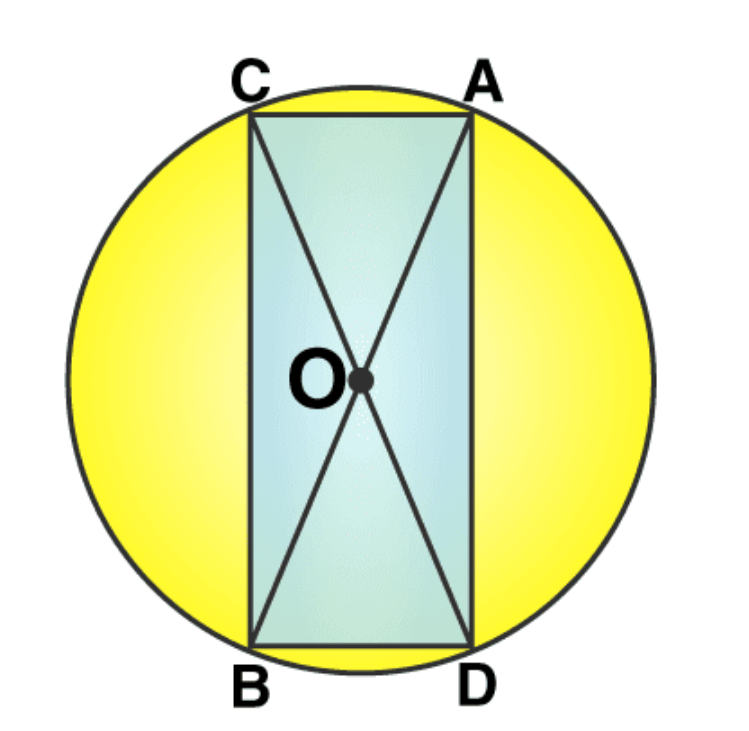 We know that the diameter of a circle are equal in length, hence quadrilateral formed will be having its diagonals of equal length.
Also, OA = OB = OC = OD = radius r and if a quadrilateral has its diagonals of same length bisecting each other. It will be a rectangle.
Let DE and FG be the diameters of the circle such that both are perpendicular to each other. Now we can find that a quadrilateral is formed by joining the ends of these diameters.
We know that the diameter of a circle are equal in length, hence quadrilateral formed will be having its diagonals of equal length.
Also, OA = OB = OC = OD = radius r and if a quadrilateral has its diagonals of same length bisecting each other. It will be a rectangle.
Let DE and FG be the diameters of the circle such that both are perpendicular to each other. Now we can find that a quadrilateral is formed by joining the ends of these diameters.
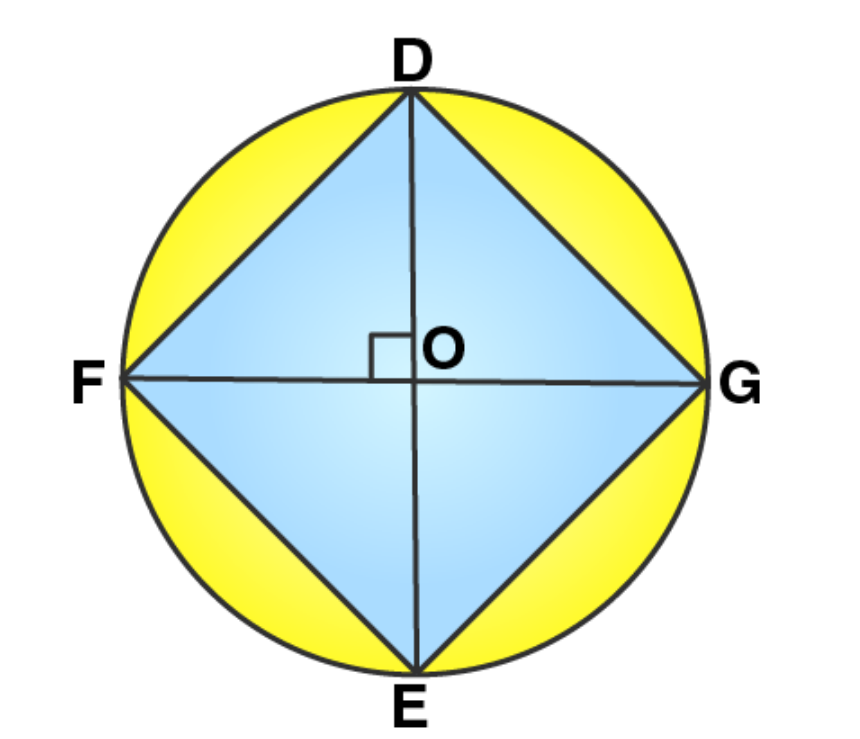 We may find that OD = OE = OF = OG = radius r.
In this quadrilateral DFEG, diagonals are equal and perpendicular to each other. Also they are bisecting each other, hence it will be a square.
To check our answers we may measure the length of sides of quadrilateral formed.
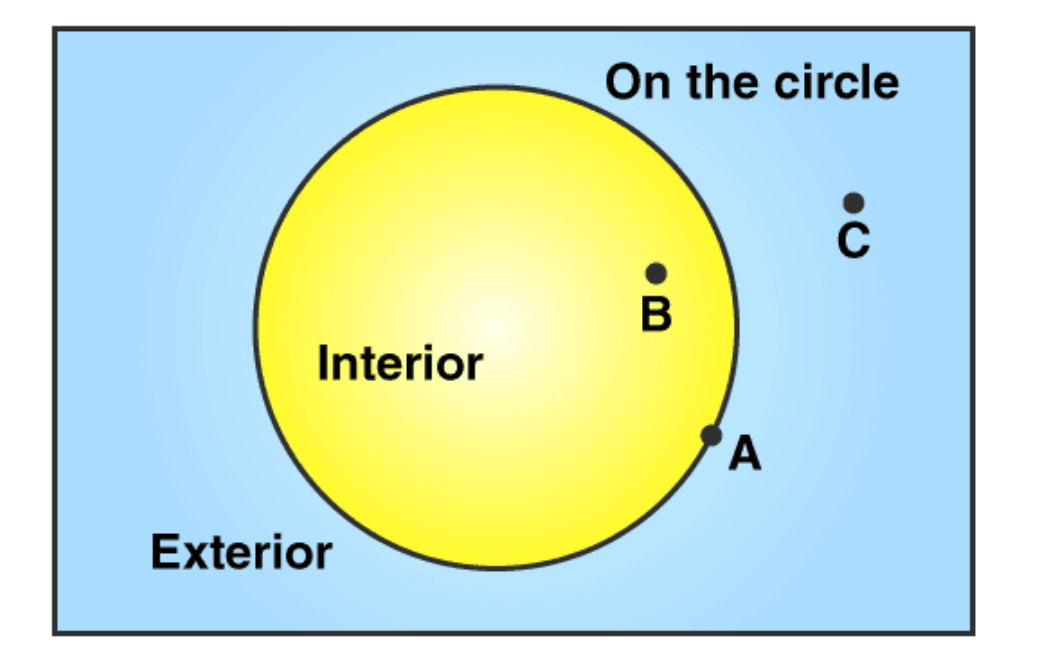
4. Draw any circle and mark points A, B and C such that
(a) A is on the circle.
(b) B is in the interior of the circle.
(c) C is in the exterior of the circle.
Solutions:
We may draw a circle and three required points A, B, C as follows:
We may find that OD = OE = OF = OG = radius r.
In this quadrilateral DFEG, diagonals are equal and perpendicular to each other. Also they are bisecting each other, hence it will be a square.
To check our answers we may measure the length of sides of quadrilateral formed.
4. Draw any circle and mark points A, B and C such that
(a) A is on the circle.
(b) B is in the interior of the circle.
(c) C is in the exterior of the circle.
Solutions:
We may draw a circle and three required points A, B, C as follows:
 5. Let A, B be the centres of two circles of equal radii; draw them so that each one of them passes through the centre of the other. Let them intersect at C and D. Examine whether
and
are at right angles.
Solutions:
Let us draw two circles having with same radius which are passing through the centre of the other circle.
5. Let A, B be the centres of two circles of equal radii; draw them so that each one of them passes through the centre of the other. Let them intersect at C and D. Examine whether
and
are at right angles.
Solutions:
Let us draw two circles having with same radius which are passing through the centre of the other circle.
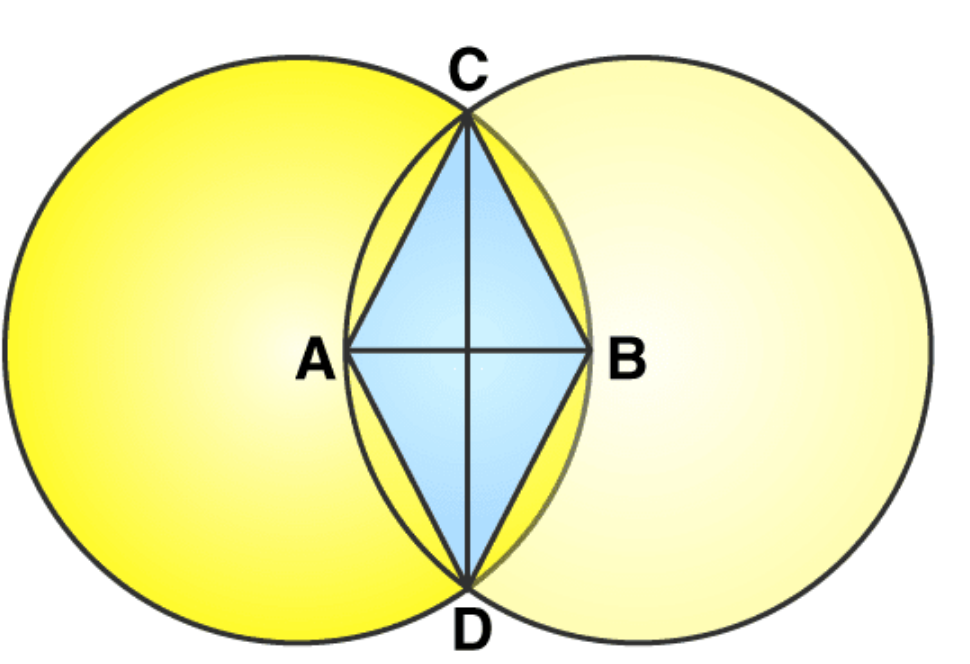 Here points A and B are the centres of these circles and these circles are intersecting each other at points C and D, respectively.
Now in quadrilateral ADBC, we may observe that:
AD = AC [radius of circle cantered at A]
BC = BD [radius of circle cantered at B]
Since, radius of both the circles are equal.
Therefore AD = AC = BC = BD
Hence quadrilateral ADBC is a rhombus and in rhombus diagonals bisect each other at 90 degree
.
Here points A and B are the centres of these circles and these circles are intersecting each other at points C and D, respectively.
Now in quadrilateral ADBC, we may observe that:
AD = AC [radius of circle cantered at A]
BC = BD [radius of circle cantered at B]
Since, radius of both the circles are equal.
Therefore AD = AC = BC = BD
Hence quadrilateral ADBC is a rhombus and in rhombus diagonals bisect each other at 90 degree
.
CBSE Board Exam Centre List 2024
Exercise 14.2 Page No: 278 1. Draw a line segment of length 7.3 cm using a ruler. Solutions: Using a ruler, we can draw a line segment of length 7.3 cm as follows Step 1: Mark a point A on the sheet Step 2: Place 0 mark of ruler at point A Step 3: At 7.3 cm on ruler, mark a point B on the sheet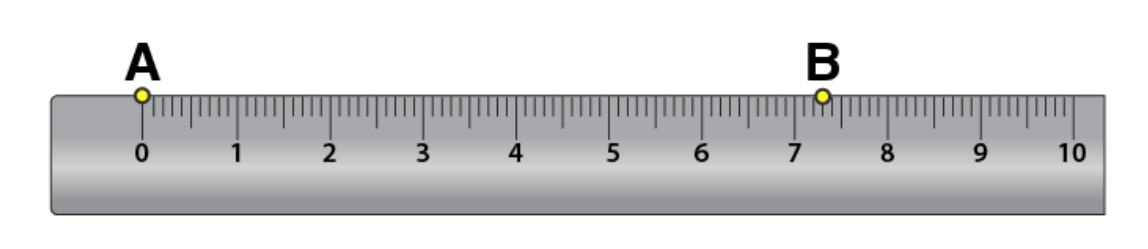 Step 4: Now join A and B
Here
Step 4: Now join A and B
Here
 2. Construct a line segment of length 5.6 cm using ruler and compasses.
Solutions:
By using a ruler and compasses, we may draw a line segment of length 5.6 cm as follows
Step 1: Draw a line l and mark a point A on this line l.
2. Construct a line segment of length 5.6 cm using ruler and compasses.
Solutions:
By using a ruler and compasses, we may draw a line segment of length 5.6 cm as follows
Step 1: Draw a line l and mark a point A on this line l.
 Step 2: On the zero mark of the ruler, place the compasses. Now extend the compasses to place the pencil up to the 5.6 cm and mark.
Step 2: On the zero mark of the ruler, place the compasses. Now extend the compasses to place the pencil up to the 5.6 cm and mark.
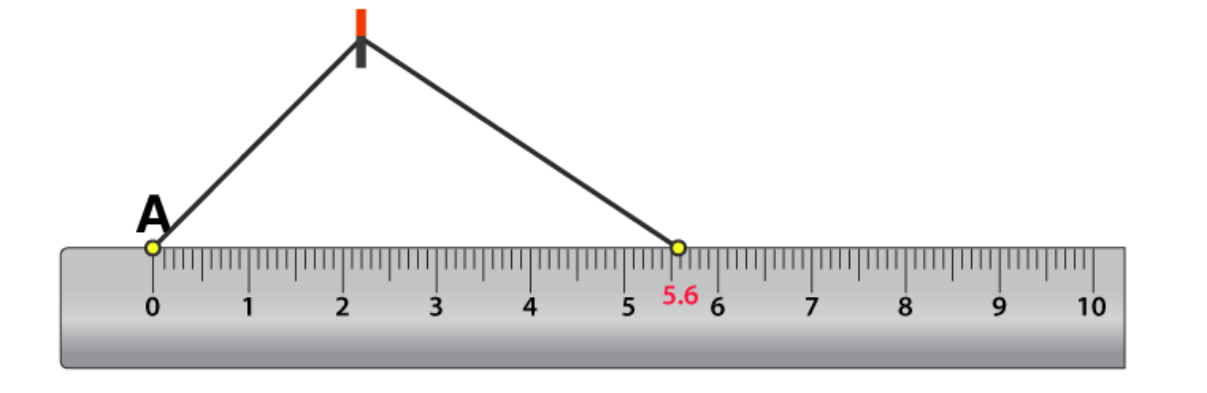 Step 3: Place the pointer of compasses on point A and draw an arc to cut l at B. Now,
Step 3: Place the pointer of compasses on point A and draw an arc to cut l at B. Now,
 3. Construct
3. Construct
 Step 2: By adjusting the compasses up to 7.8 cm, while putting the pointer of compasses on point A draw an arc to cut l on B
Step 2: By adjusting the compasses up to 7.8 cm, while putting the pointer of compasses on point A draw an arc to cut l on B
 Step 3: By adjusting the compasses up to 4.7 cm, draw an arc to cut l on C, while putting the pointer of compasses on point A.
Step 3: By adjusting the compasses up to 4.7 cm, draw an arc to cut l on C, while putting the pointer of compasses on point A.
 Step 4: Now, place the ruler in such a way that 0 mark of the ruler will match with the point C.
Step 4: Now, place the ruler in such a way that 0 mark of the ruler will match with the point C.
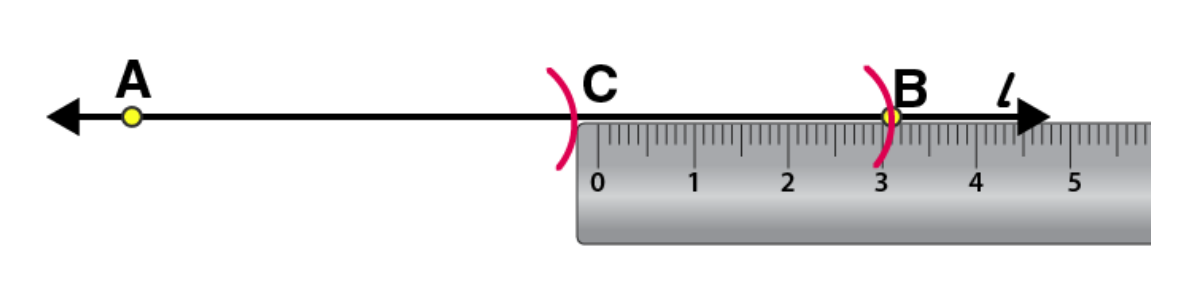 Now read the position of point B. It will be 3.1 cm.
Now read the position of point B. It will be 3.1 cm.
 Solutions:
We can draw a line segment
Solutions:
We can draw a line segment
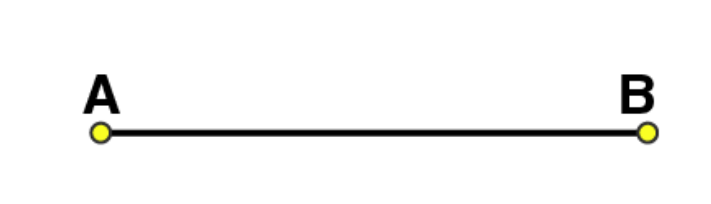
 (2)
By adjusting the compasses up to the length of AB, place the pointer of compasses at point P and draw an arc to cut the line at X.
(2)
By adjusting the compasses up to the length of AB, place the pointer of compasses at point P and draw an arc to cut the line at X.
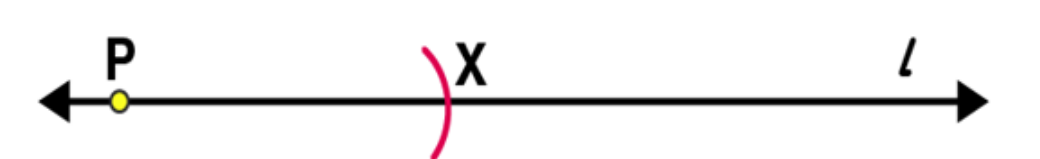 (3)
Again place the pointer on point X, draw an arc to cut line l at point Q.
(3)
Again place the pointer on point X, draw an arc to cut line l at point Q.
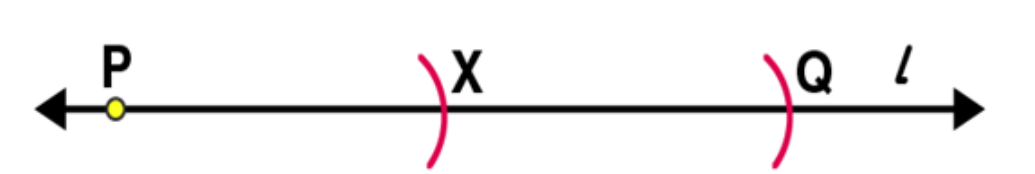
 (2)
Adjust the compasses up to the length of CD and put the pointer of compasses at point A, draw an arc to cut AB at point P.
(2)
Adjust the compasses up to the length of CD and put the pointer of compasses at point A, draw an arc to cut AB at point P.
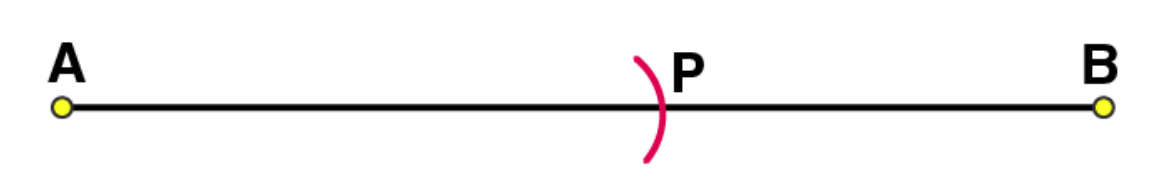 (3)
Adjust the compasses up to the length of PB. Draw a line l and mark a point X on it.
(3)
Adjust the compasses up to the length of PB. Draw a line l and mark a point X on it.
 (4)
By placing the pointer of compasses at point X, draw an arc to cut the line at Y.
(4)
By placing the pointer of compasses at point X, draw an arc to cut the line at Y.

| CBSE Syllabus Class 6 | |
| CBSE Class 6 Science Syllabus | CBSE Class 6 Maths Syllabus |
| CBSE Class 6 Social Science Syllabus | CBSE Class 6 English Syllabus |
 (2)
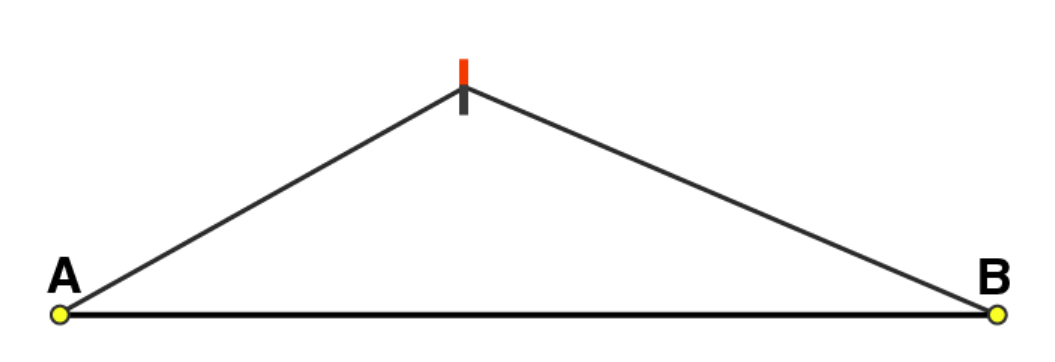
Adjust the compasses up to the length of
(2)
Adjust the compasses up to the length of
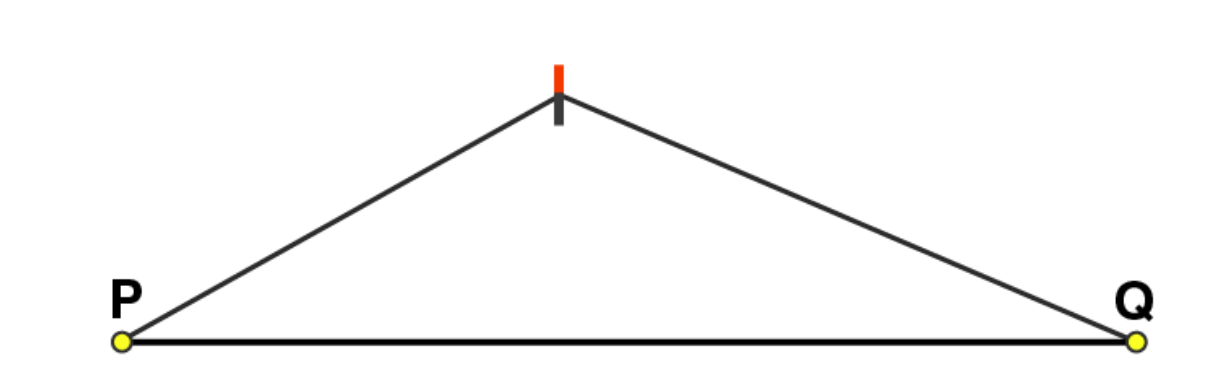 (3)
Draw any line l and mark a point A on it
(3)
Draw any line l and mark a point A on it
 (4)
Place the pointer on point A, without changing the setting of compasses, draw an arc to cut the line segment at B point.
(4)
Place the pointer on point A, without changing the setting of compasses, draw an arc to cut the line segment at B point.
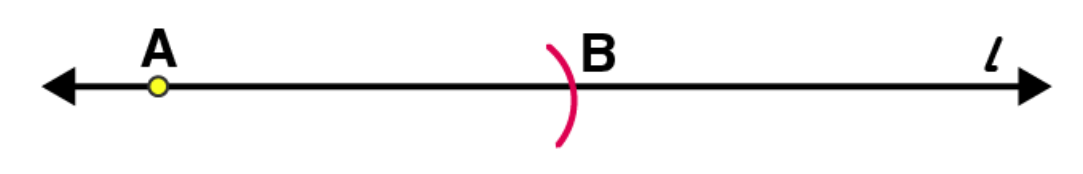
 (2)
Adjust the compasses up to the length of
(2)
Adjust the compasses up to the length of
 (3)
Draw a line l and mark a point P on it
(3)
Draw a line l and mark a point P on it
 (4)
Place the pointer on P, draw an arc to cut the line segment at point X, without changing the setting of compasses
(4)
Place the pointer on P, draw an arc to cut the line segment at point X, without changing the setting of compasses
 (5)
Again with same radius as before, by placing the pointer on point X, draw an arc to cut the line l at point Q
(5)
Again with same radius as before, by placing the pointer on point X, draw an arc to cut the line l at point Q
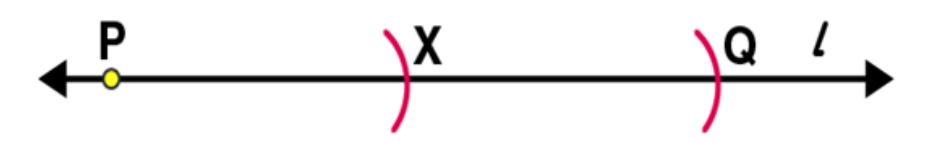 Exercise 14.4 Page No: 284
1. Draw any line segment
Exercise 14.4 Page No: 284
1. Draw any line segment
 (2)
Taking M as centre and a convenient radius, construct an arc intersecting the line segment
at points C and D, respectively.
(2)
Taking M as centre and a convenient radius, construct an arc intersecting the line segment
at points C and D, respectively.
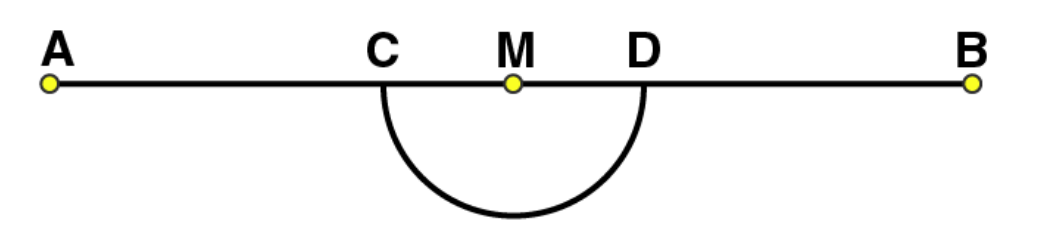 (3)
By taking centres as C and D and radius greater than CM, construct two arcs such that they intersect each other at point E.
(3)
By taking centres as C and D and radius greater than CM, construct two arcs such that they intersect each other at point E.
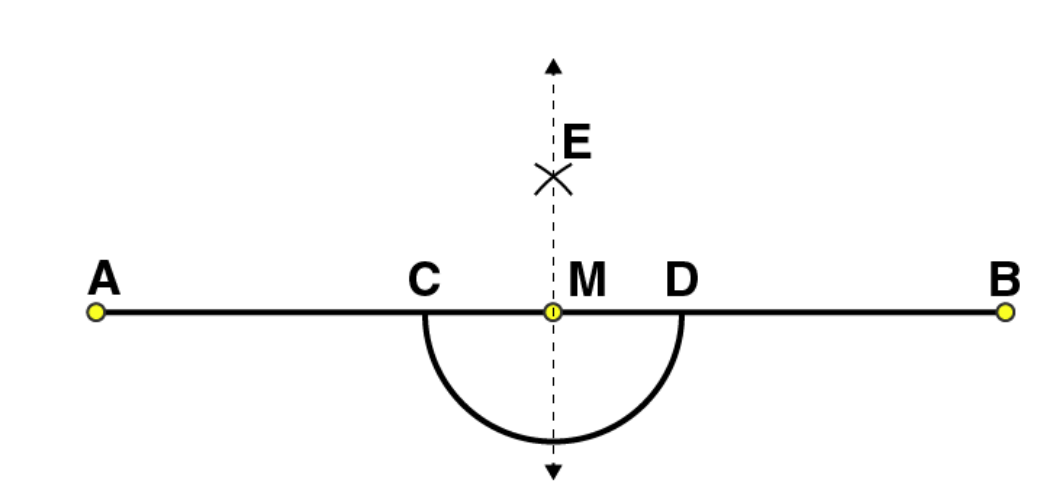
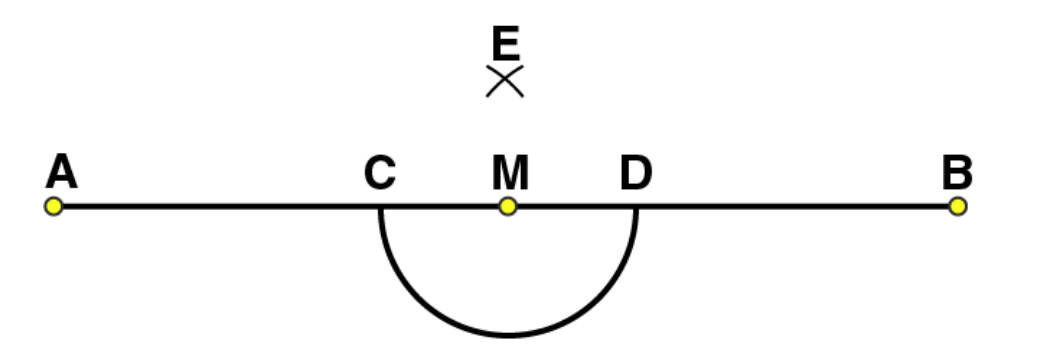 (4)
Join EM. Now
is perpendicular to
(4)
Join EM. Now
is perpendicular to
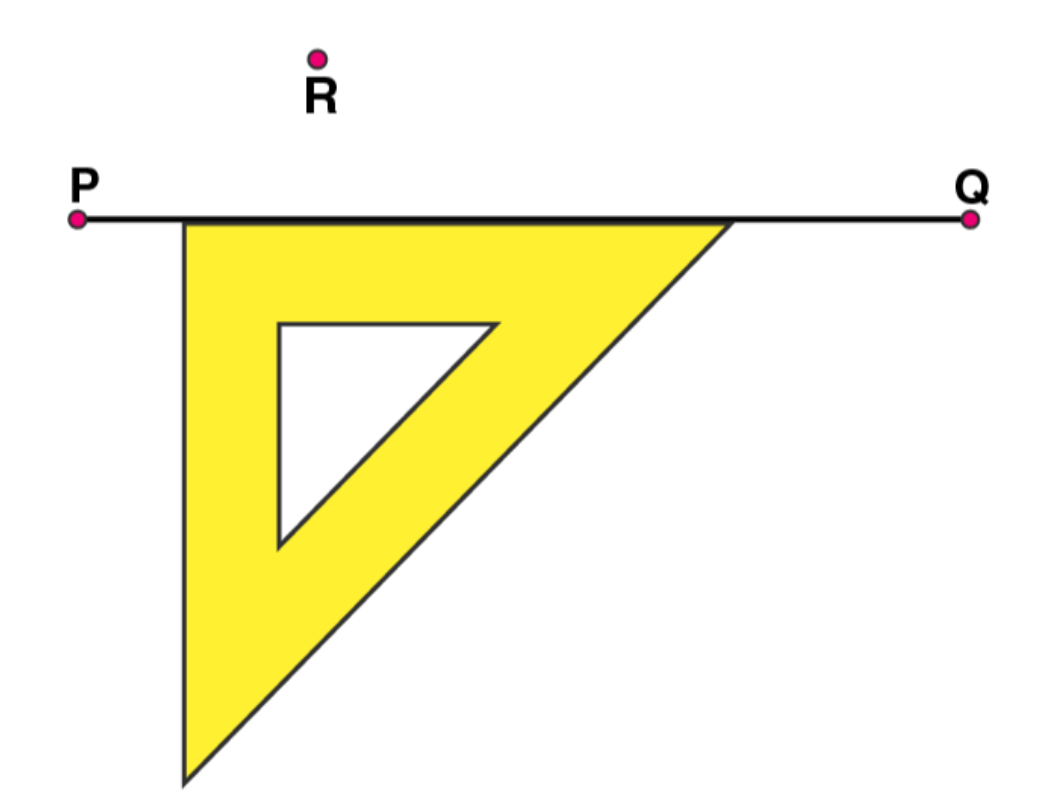
 2. Draw any line segment
2. Draw any line segment
 (2)
Place a set square on
(2)
Place a set square on
 (3)
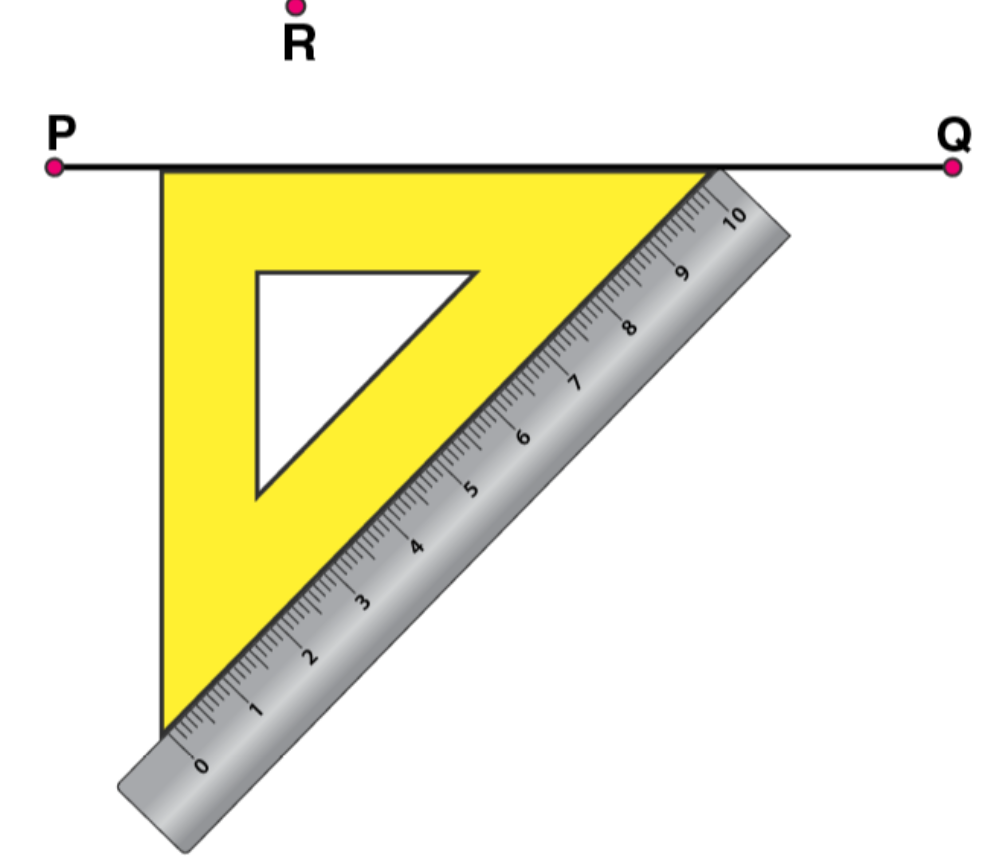
Now, place the ruler along the edge opposite to right angle of set square.
(3)
Now, place the ruler along the edge opposite to right angle of set square.
 (4)
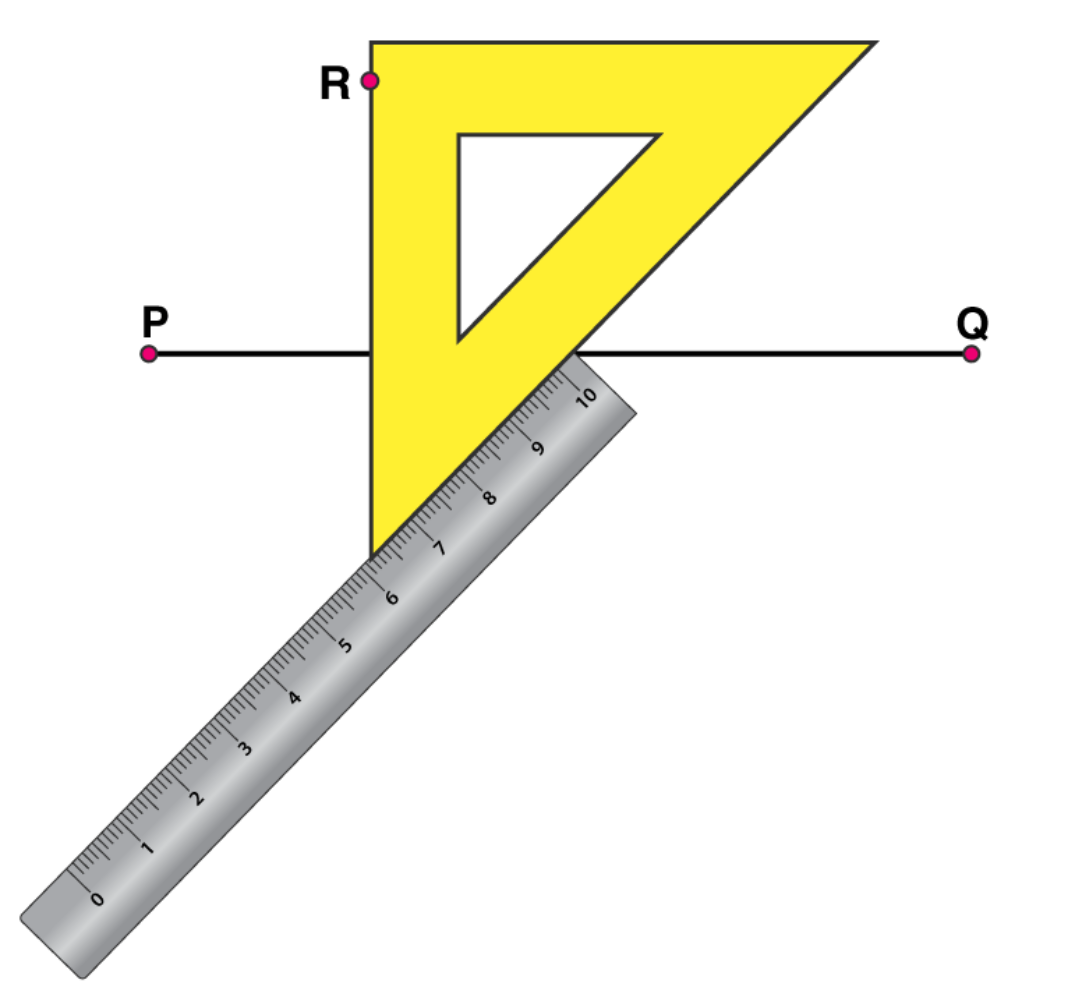
Hold the ruler fixed. Slide the set square along the ruler such that the point R touches the other arm of set square.
(4)
Hold the ruler fixed. Slide the set square along the ruler such that the point R touches the other arm of set square.
 (5)
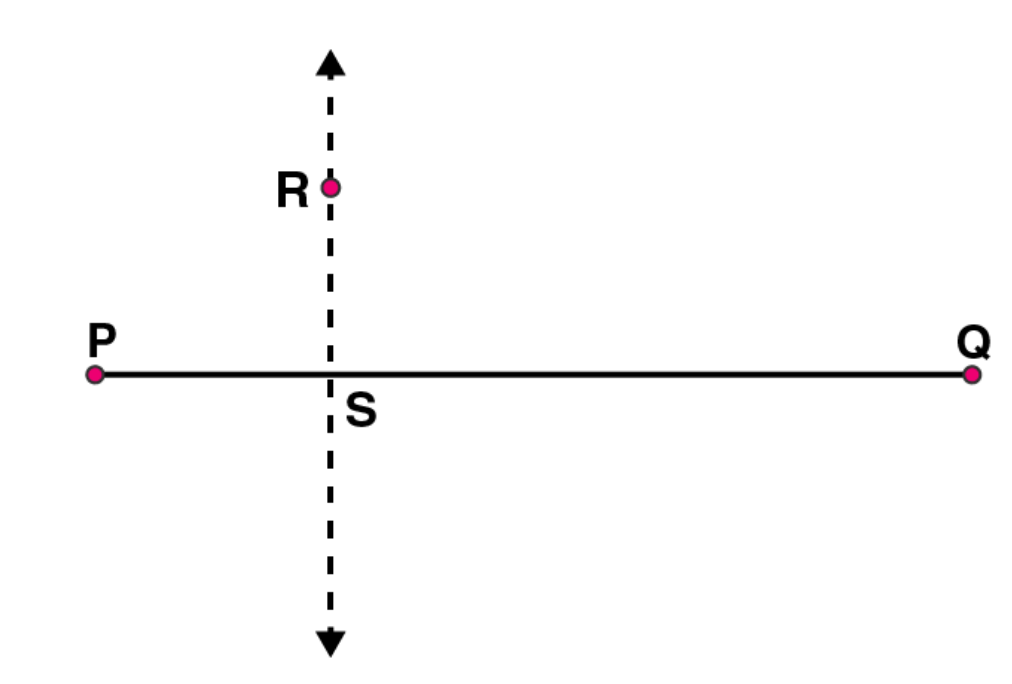
Draw a line along this edge of set square which passes through point R. Now, it is the required line perpendicular to
(5)
Draw a line along this edge of set square which passes through point R. Now, it is the required line perpendicular to
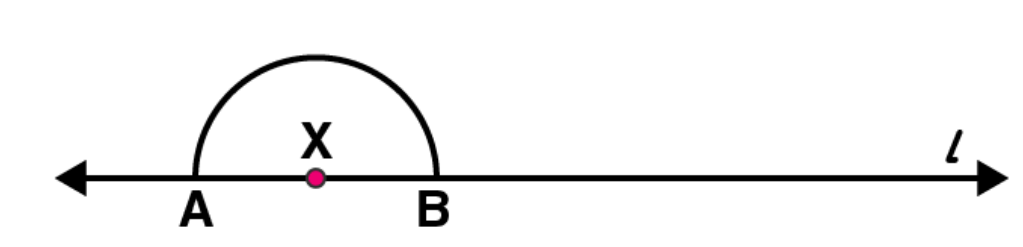
 3. Draw a line l and a point X on it. Through X, draw a line segment
3. Draw a line l and a point X on it. Through X, draw a line segment
 (2)
By taking X as centre and with a convenient radius, draw an arc intersecting the line l at points A and B, respectively.
(2)
By taking X as centre and with a convenient radius, draw an arc intersecting the line l at points A and B, respectively.
 (3)
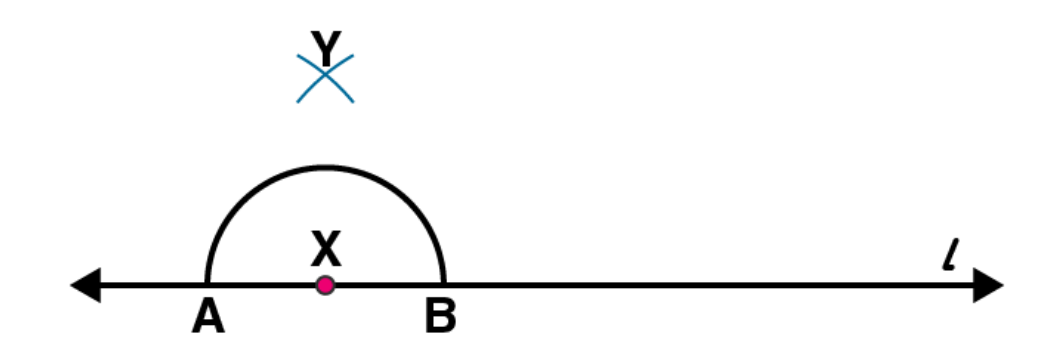
With A and B as centres and a radius more than AX, construct two arcs such that they intersect each other at point Y.
(3)
With A and B as centres and a radius more than AX, construct two arcs such that they intersect each other at point Y.
 (4)
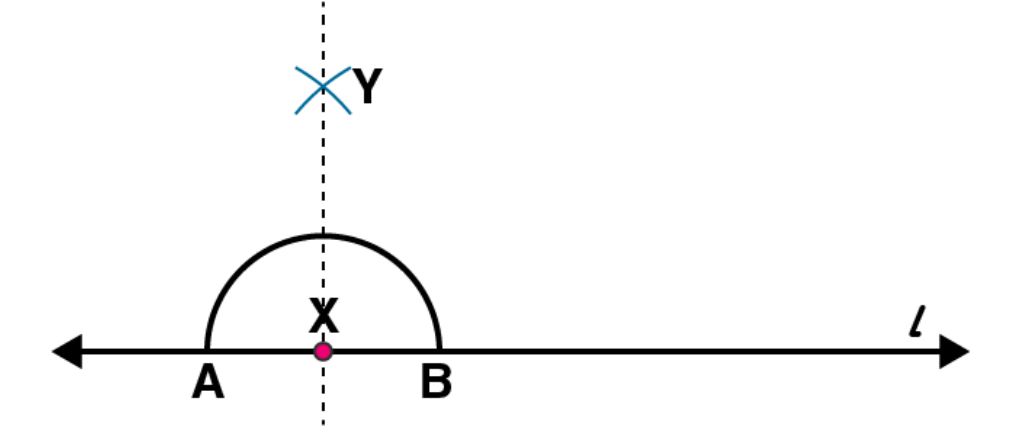
Join XY. Here
is perpendicular to l
(4)
Join XY. Here
is perpendicular to l
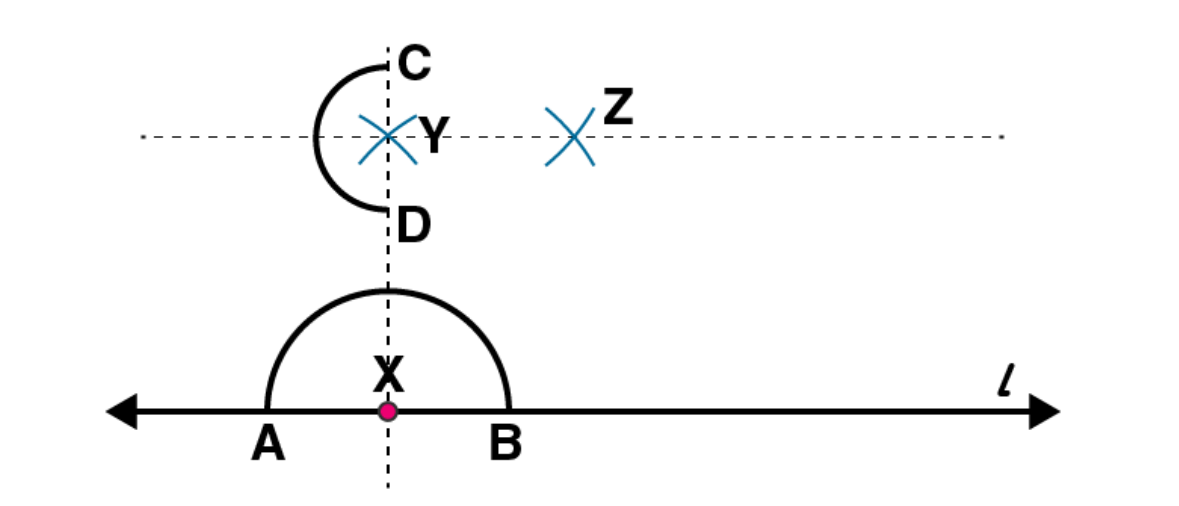
 Similarly, by taking C and D as centres and radius more than CY, construct two arcs intersecting at point Z. Join ZY. The line
is perpendicular to
Similarly, by taking C and D as centres and radius more than CY, construct two arcs intersecting at point Z. Join ZY. The line
is perpendicular to
| Related Links |
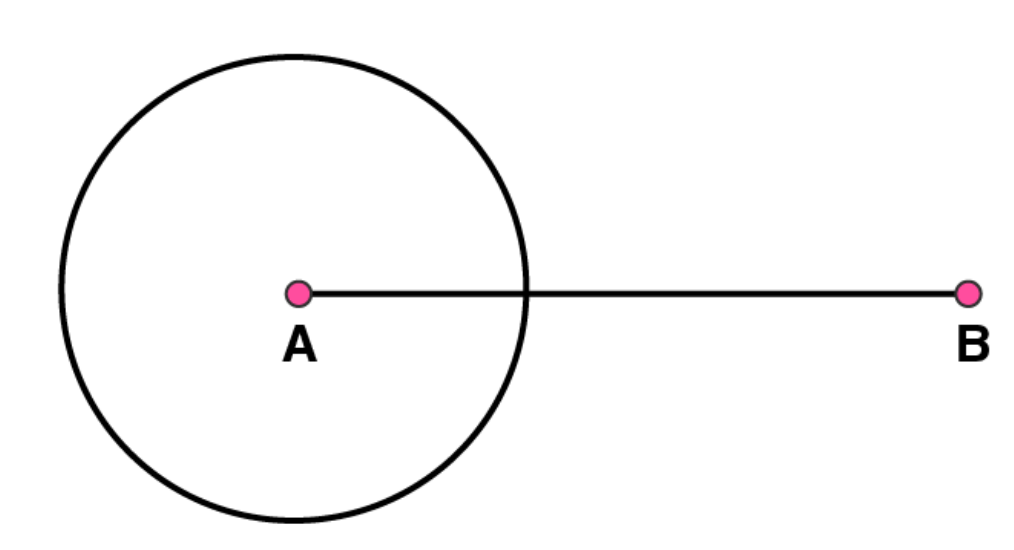
 (2)
Take A as centre and draw a circle by using compasses. The radius of circle should be more than half the length of
(2)
Take A as centre and draw a circle by using compasses. The radius of circle should be more than half the length of
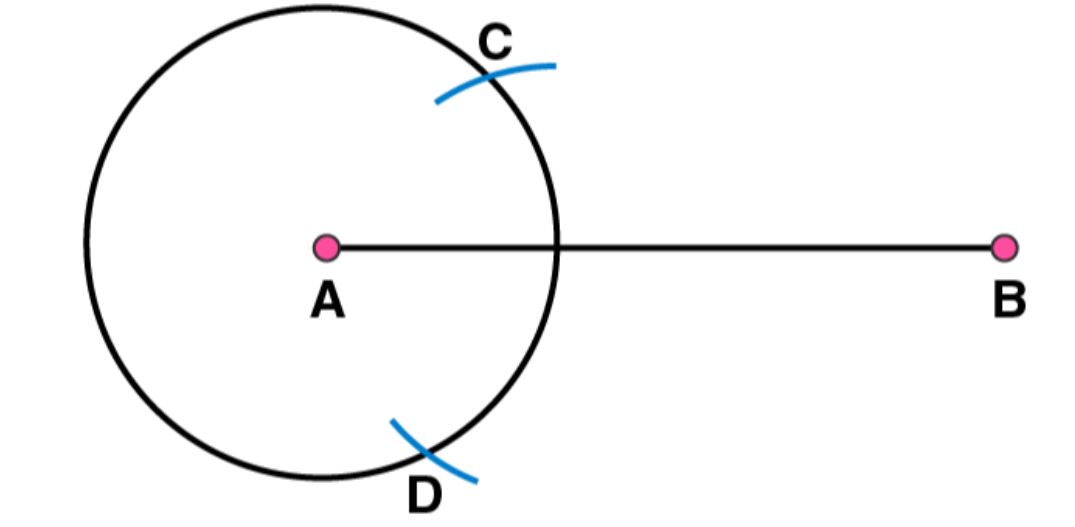
 (3)
Now, take B as centre and draw another circle using compasses with the same radius as before. Let it cut the previous circle at points C and D
(3)
Now, take B as centre and draw another circle using compasses with the same radius as before. Let it cut the previous circle at points C and D
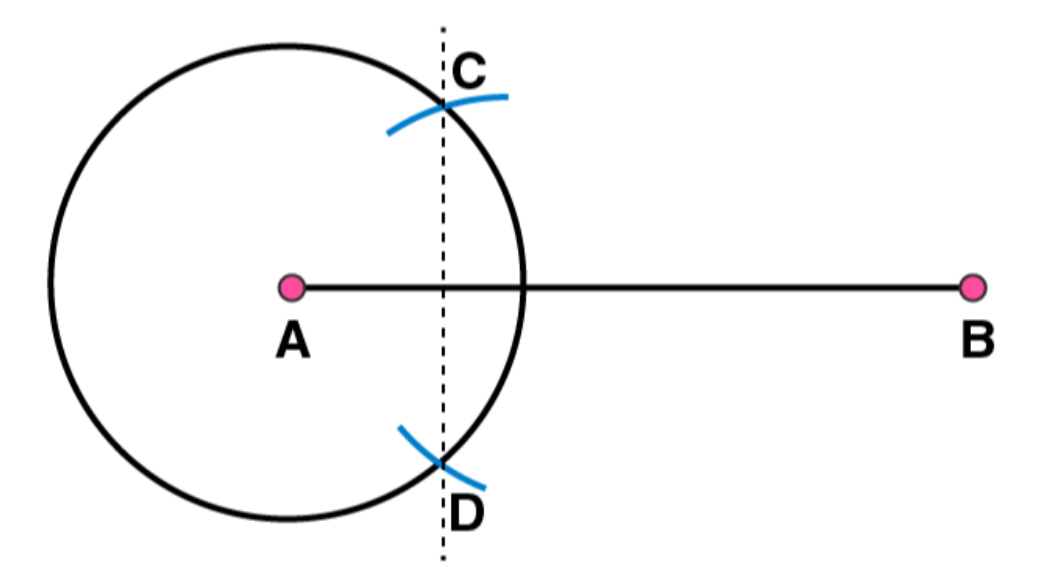
 (4)
Join CD. Now
(4)
Join CD. Now
 2. Draw a line segment of length 9.5 cm and construct its perpendicular bisector.
Solutions:
Following steps are observed to construct a line segment of length 9.5 cm and to construct its perpendicular bisector
(1)
Draw a line segment
of 9.5 cm
2. Draw a line segment of length 9.5 cm and construct its perpendicular bisector.
Solutions:
Following steps are observed to construct a line segment of length 9.5 cm and to construct its perpendicular bisector
(1)
Draw a line segment
of 9.5 cm

(2) Take point P as centre and draw a circle by using compasses. The radius of circle should be more than half the length of PQ
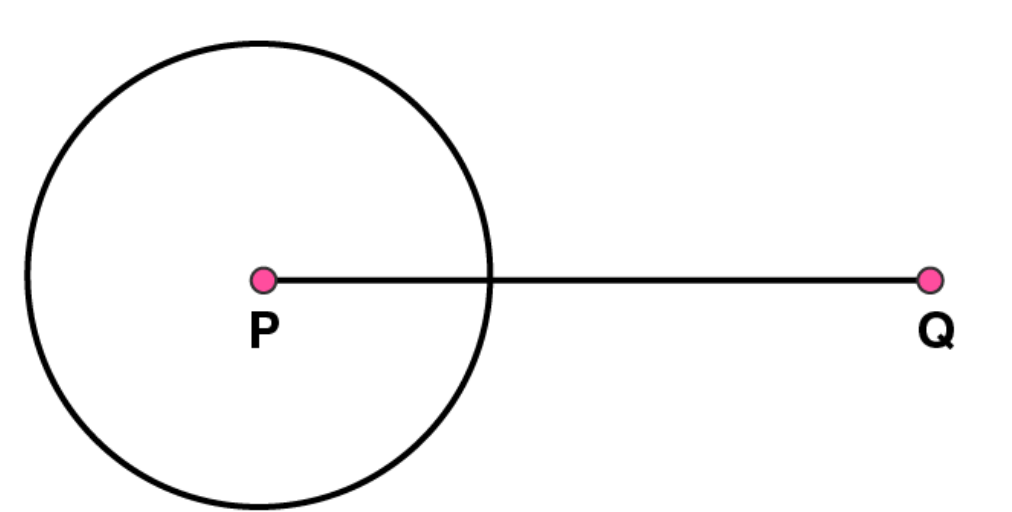 (3)
Taking the centre at point Q, again draw another circle using compasses with the same radius as before. Let it cut the previous circle at R and S respectively.
(3)
Taking the centre at point Q, again draw another circle using compasses with the same radius as before. Let it cut the previous circle at R and S respectively.
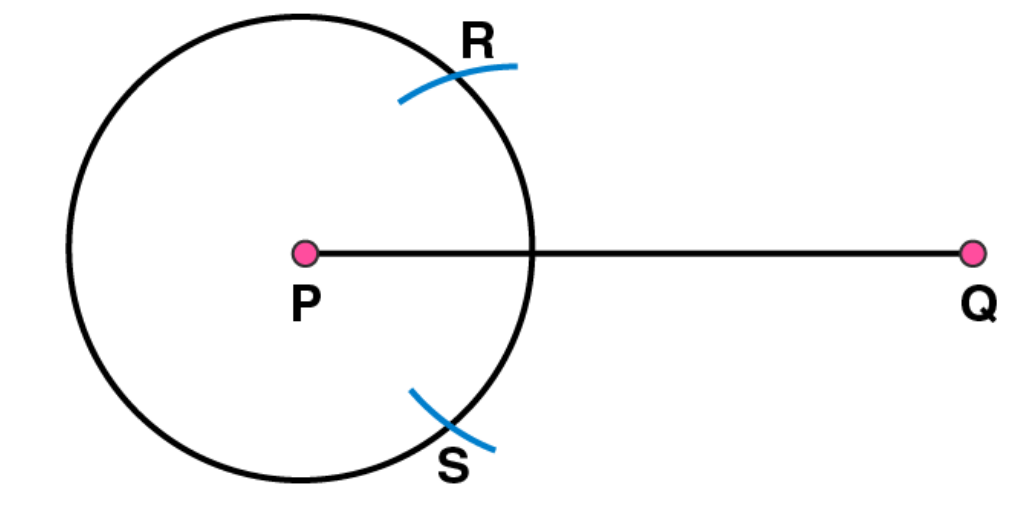 (4)
Join RS. Now, RS
is the axis of symmetry i.e. the perpendicular bisector of the line PQ
(4)
Join RS. Now, RS
is the axis of symmetry i.e. the perpendicular bisector of the line PQ
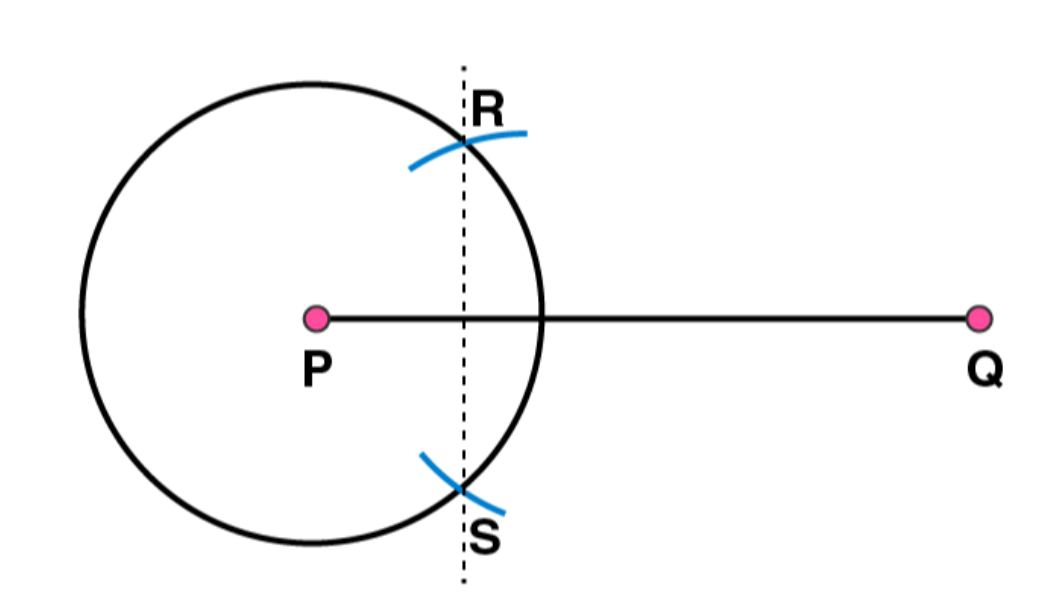 3. Draw the perpendicular bisector of
whose length is 10.3 cm.
(a) Take any point P on the bisector drawn. Examine whether PX = PY.
(b) If M is the mid point of
, what can you say about the lengths MX and XY?
Solutions:
(1)
Draw a line segment
of 10.3 cm
3. Draw the perpendicular bisector of
whose length is 10.3 cm.
(a) Take any point P on the bisector drawn. Examine whether PX = PY.
(b) If M is the mid point of
, what can you say about the lengths MX and XY?
Solutions:
(1)
Draw a line segment
of 10.3 cm
 (2)
Take point X as centre and draw a circle by using compasses. The radius of circle should be more than half the length of XY
(2)
Take point X as centre and draw a circle by using compasses. The radius of circle should be more than half the length of XY
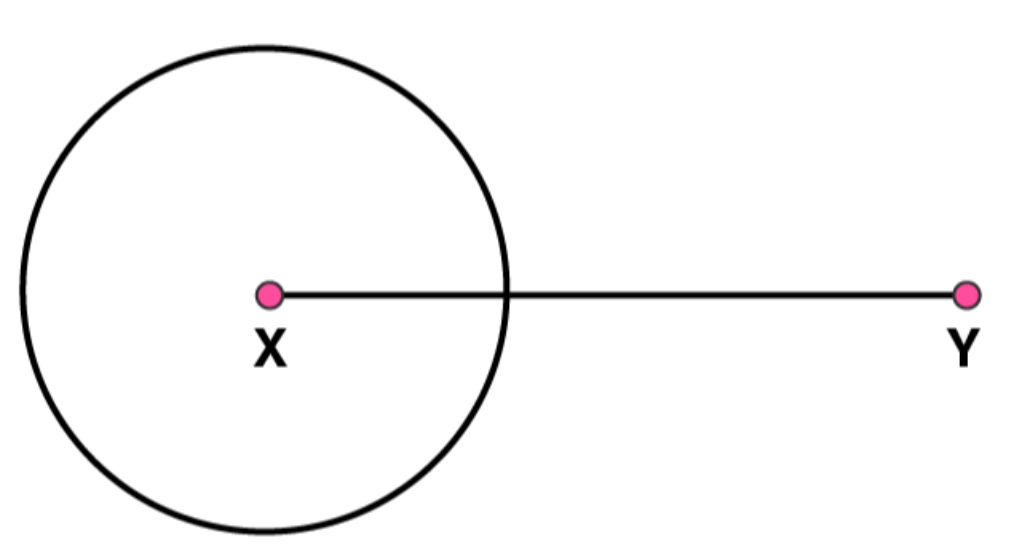 (3)
Now taking Y as centre, draw another circle using compasses with the same radius as before. Let it cut at previous circle at points A and B
(3)
Now taking Y as centre, draw another circle using compasses with the same radius as before. Let it cut at previous circle at points A and B
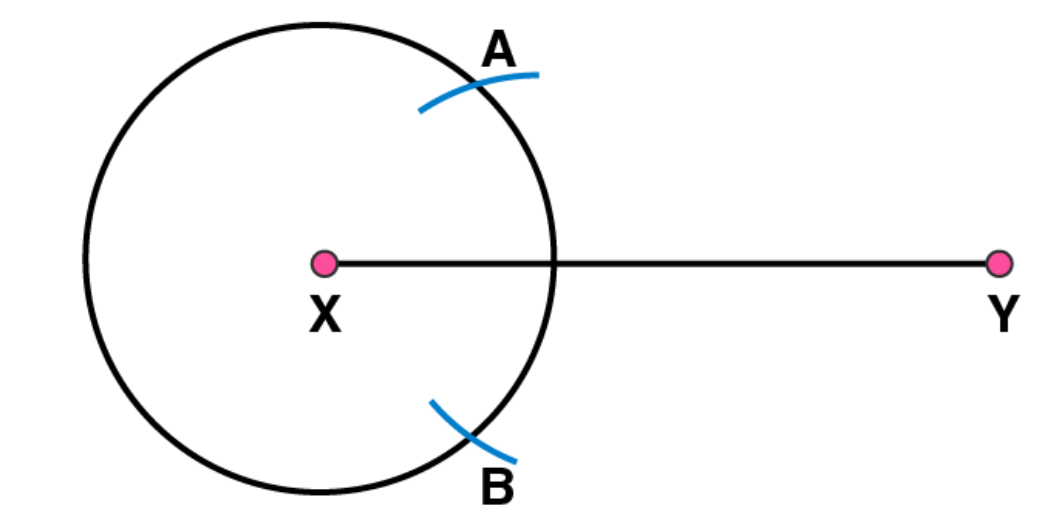 (4)
Join AB. Here AB
is the axis of symmetry
(4)
Join AB. Here AB
is the axis of symmetry
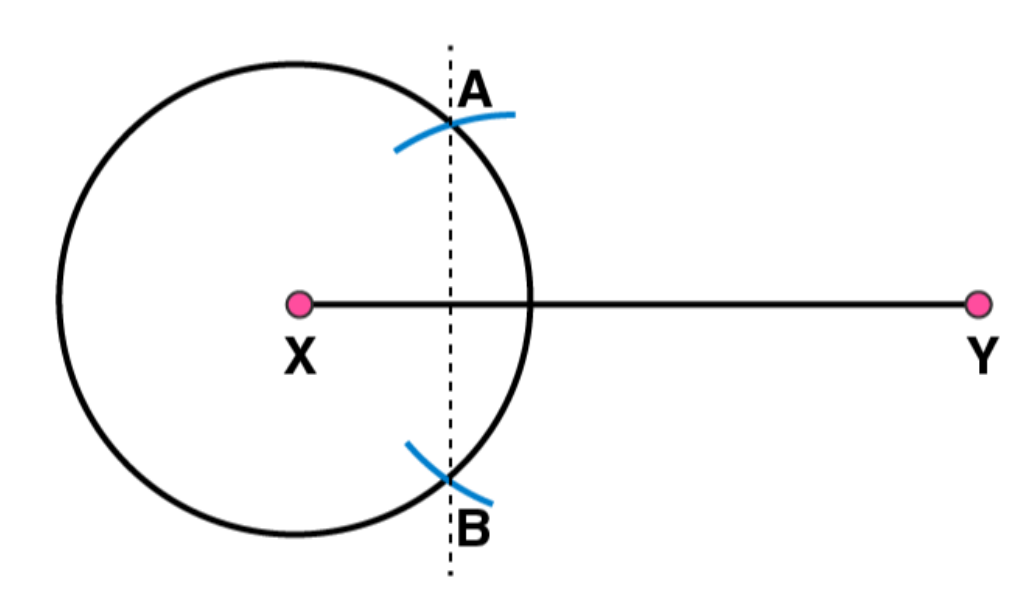 (a)
Take any point P on AB
. We may observe that the measure of lengths of PX and PY are same AB
being the axis of symmetry, any point lying on
will be at same distance from the both ends of
(a)
Take any point P on AB
. We may observe that the measure of lengths of PX and PY are same AB
being the axis of symmetry, any point lying on
will be at same distance from the both ends of
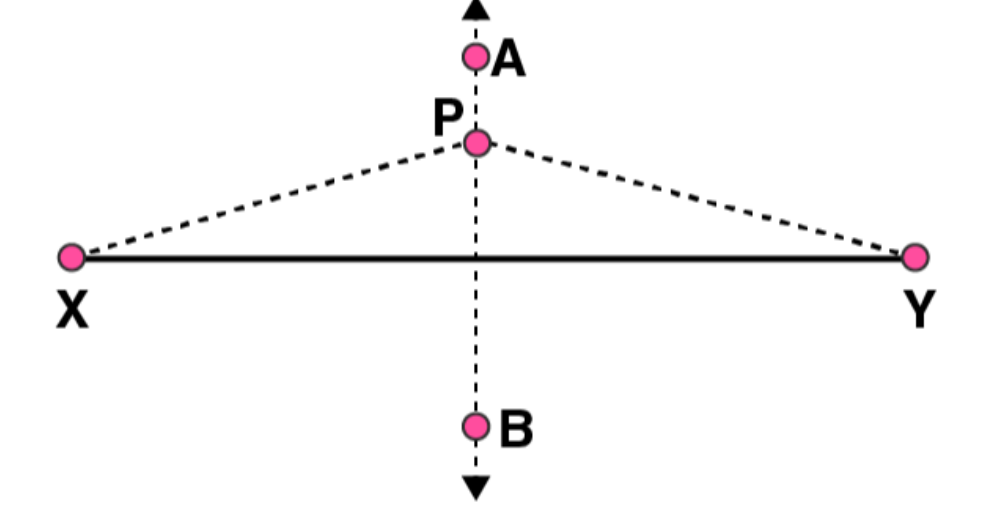 (b)
M is the midpoint of XY
. Perpendicular bisector AB
will be passing through point M. Hence length of XY
is double of MX
or 2MX = XY.
(b)
M is the midpoint of XY
. Perpendicular bisector AB
will be passing through point M. Hence length of XY
is double of MX
or 2MX = XY.
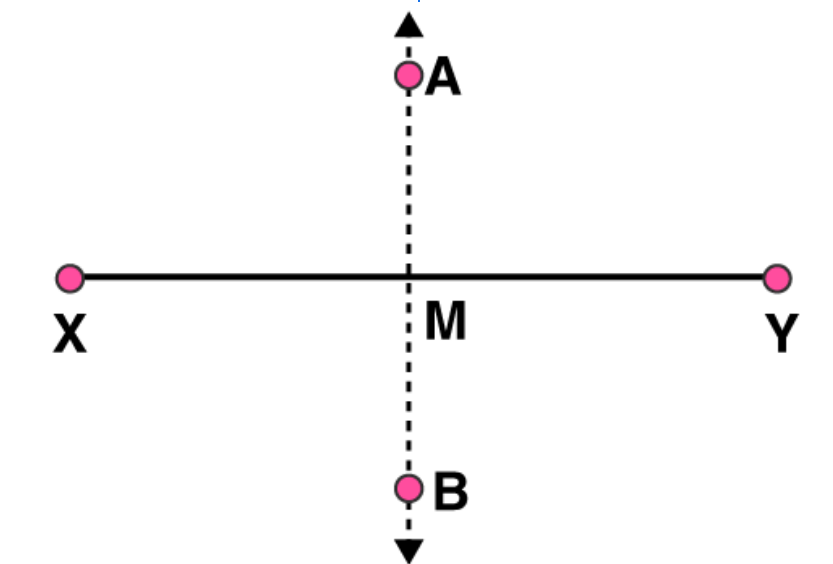 4. Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.
Solutions:
(1)
Draw a line segment XY
of 12.8 cm
4. Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.
Solutions:
(1)
Draw a line segment XY
of 12.8 cm
 (2)
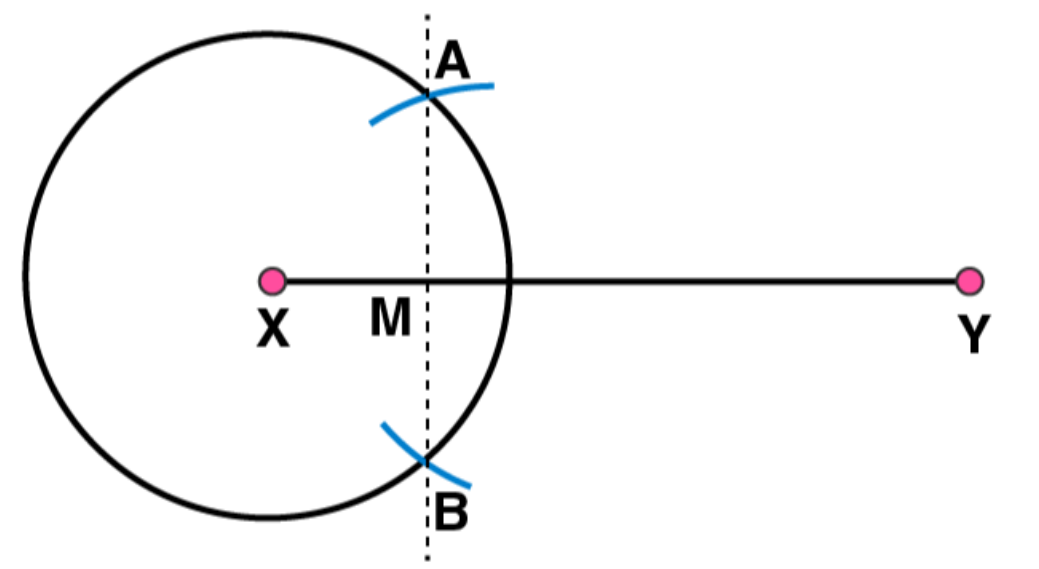
By taking point X as centre and radius more than half of XY, draw a circle.
(2)
By taking point X as centre and radius more than half of XY, draw a circle.
 (3)
Again with same radius and centre as Y, draw two arcs to cut the circle at points A and B. Join AB which intersects XY
at point M
(3)
Again with same radius and centre as Y, draw two arcs to cut the circle at points A and B. Join AB which intersects XY
at point M
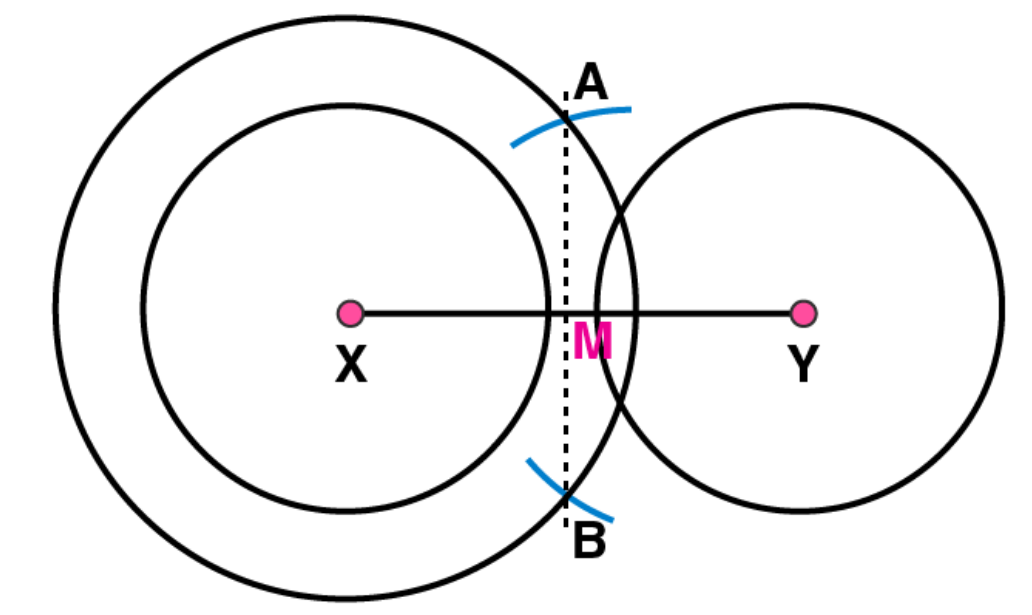
 (4)
By taking X and Y as centres, draw two circles with radius more than half of XM.
(4)
By taking X and Y as centres, draw two circles with radius more than half of XM.
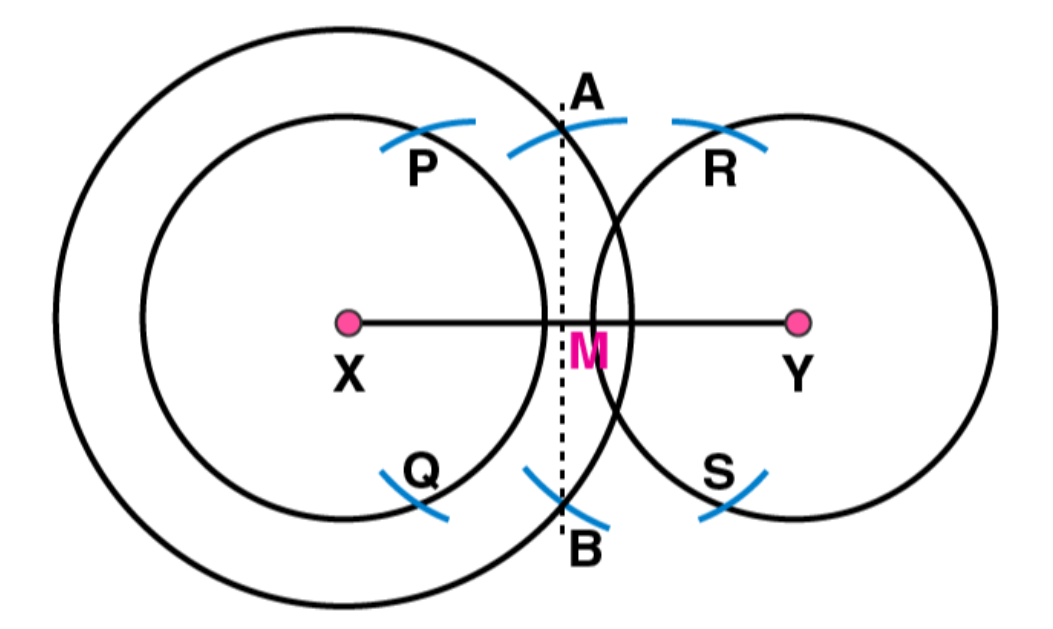
 (5)
Taking M as centre and with same radius, draw two arcs to intersect these circles at P, Q and R, S
(5)
Taking M as centre and with same radius, draw two arcs to intersect these circles at P, Q and R, S
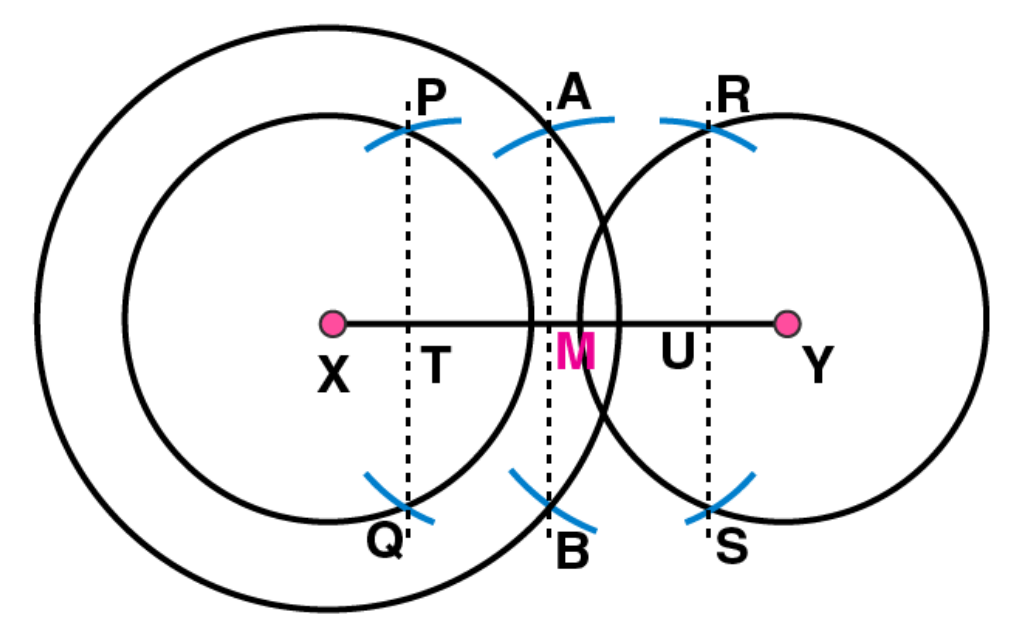
 (6)
Join PQ, and RS. These are intersecting
(6)
Join PQ, and RS. These are intersecting
 5. With
of length 6.1 cm as diameter, draw a circle.
Solutions:
(1)
Draw a line segment PQ
of 6.1 cm
5. With
of length 6.1 cm as diameter, draw a circle.
Solutions:
(1)
Draw a line segment PQ
of 6.1 cm
 (2)
Take point P as centre and radius more than half of
, draw a circle
(2)
Take point P as centre and radius more than half of
, draw a circle
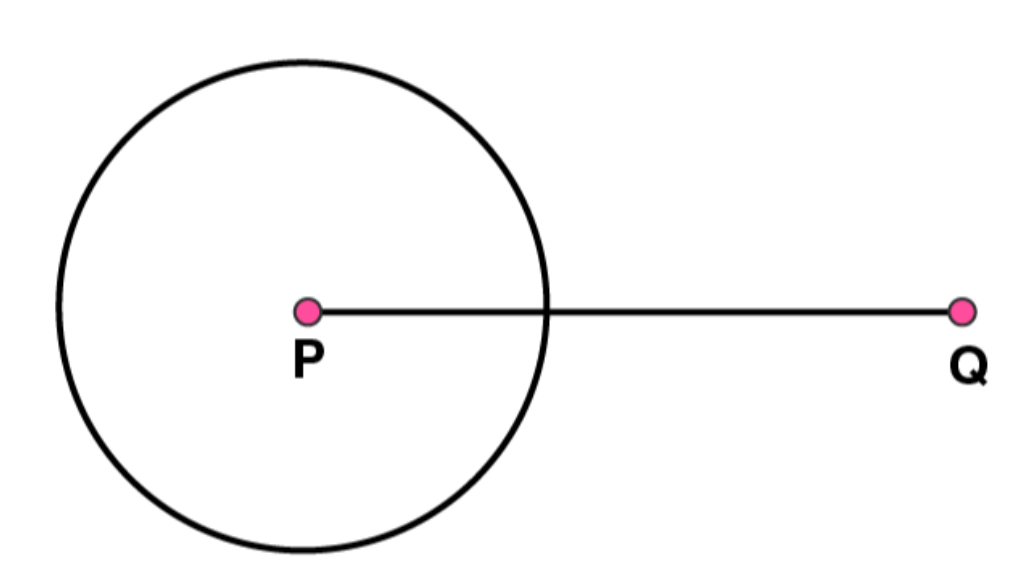 (3)
Again with same radius and Q as centre, draw two arcs intersecting the circle at points R and S
(3)
Again with same radius and Q as centre, draw two arcs intersecting the circle at points R and S
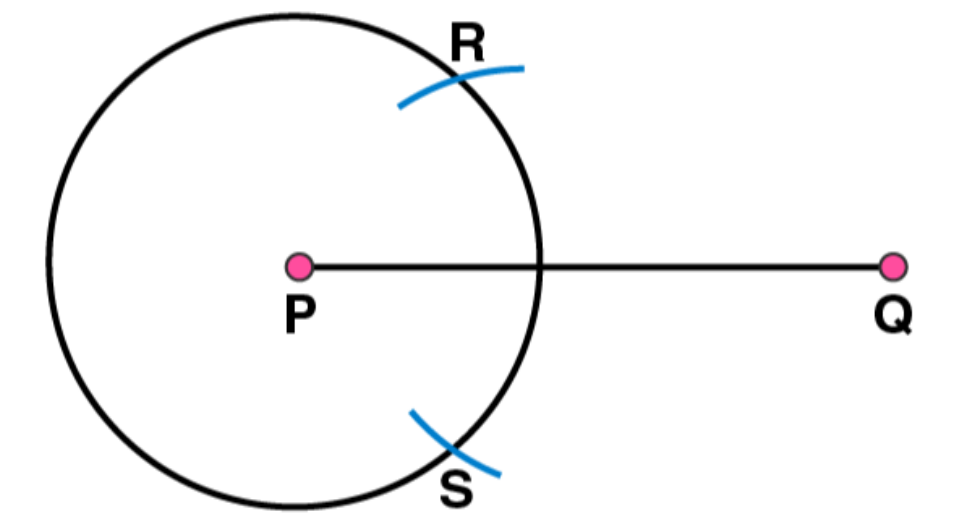 (4)
Join RS which intersects
(4)
Join RS which intersects
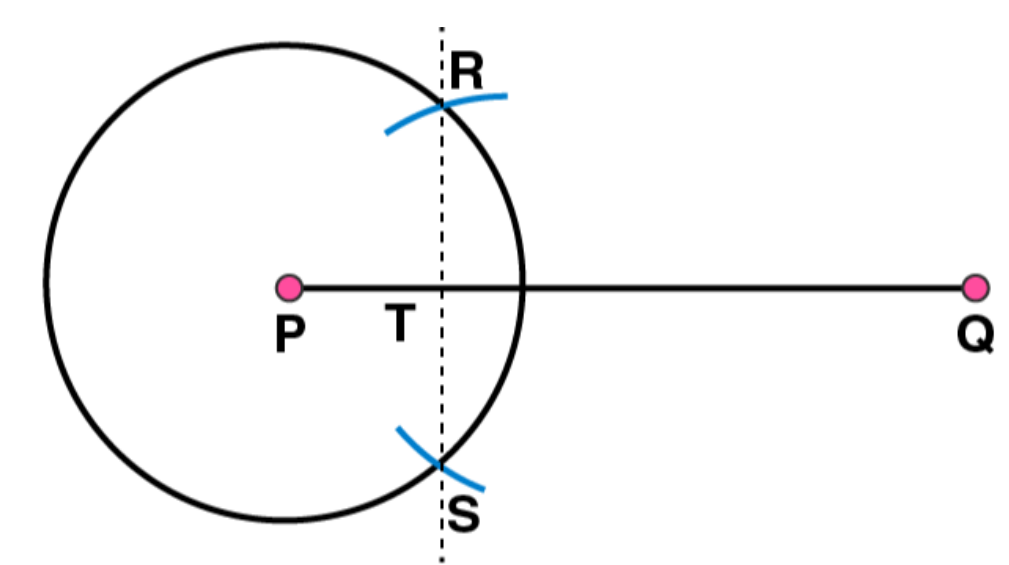 (5)
Taking the centre as T and radius TP, draw a circle which passes through Q. Now, this is the required circle.
(5)
Taking the centre as T and radius TP, draw a circle which passes through Q. Now, this is the required circle.
 6. Draw a circle with centre C and radius 3.4 cm. Draw any chord AB
. Construct the perpendicular bisector of AB
and examine if it passes through C.
Solutions:
(1)
Mark any point C on the sheet
(2)
Adjust the compasses up to 3.4 cm and by putting the pointer of compasses at point C, turn compasses slowly to draw the circle. This is the required circle of 3.4 cm radius.
6. Draw a circle with centre C and radius 3.4 cm. Draw any chord AB
. Construct the perpendicular bisector of AB
and examine if it passes through C.
Solutions:
(1)
Mark any point C on the sheet
(2)
Adjust the compasses up to 3.4 cm and by putting the pointer of compasses at point C, turn compasses slowly to draw the circle. This is the required circle of 3.4 cm radius.
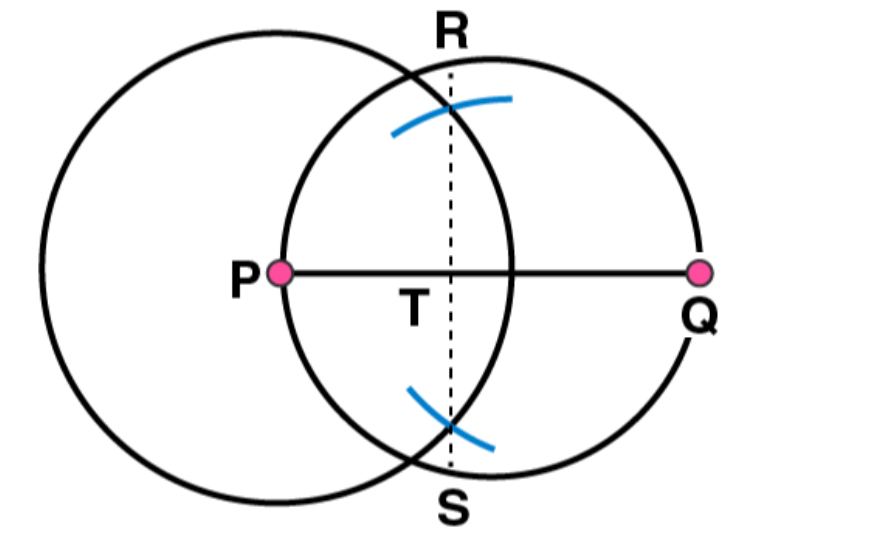
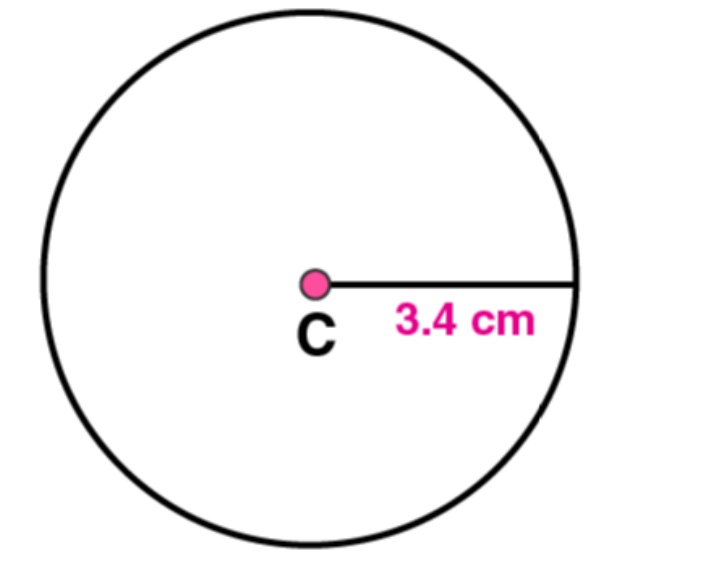 (3)
Mark any chord AB
in the circle
(3)
Mark any chord AB
in the circle
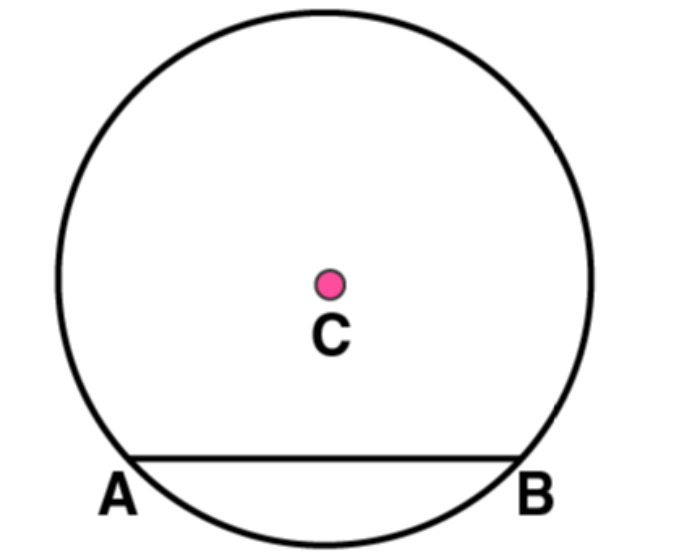
NCERT Solutions for Class 6 Maths Chapter 14 FAQs
How will I draw a circle of a definite radius?
To draw a circle of a definite radius, use a compass by placing the needle at the centre point. Extend the pencil to the desired radius and rotate the compass 360 degrees.
How will I draw one perpendicular bisector of a line segment?
Draw a perpendicular bisector of a line segment by using a compass to draw arcs on either side of the segment. Where the arcs intersect, draw a line perpendicular to the segment through that point.
Are formulae important in Practical Geometry for Class 6 Chapter 14?
Yes, formulae are crucial in Practical Geometry for Class 6 Chapter 14 as they provide the necessary steps and measurements for constructing geometric shapes accurately.
What are the basic concepts given in Class 6 Maths Chapter 14?
Class 6 Maths Chapter 14 covers basic concepts of Practical Geometry, including the construction of different geometric figures using a compass and ruler.
What is Practical Geometry in Maths?
Practical Geometry in Maths involves the construction of geometric shapes, angles, and figures using tools like a compass and ruler, focusing on hands-on applications rather than theoretical concepts.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App







