
NCERT Solutions for Class 6 Maths Chapter 11
NCERT Solutions for Class 6 Maths Chapter 11: You can easily get the NCERT Solutions for Class 6 Maths Chapter 11 Algebra for regular practice and better results. These solutions, aligned with the NCERT curriculum and CBSE Syllabus for Class 6, are created by experts. They assist students in understanding different methods to answer questions. For better exam performance, students can also use our notes and tips to quickly solve Math problems and score well in their finals. Achieving high marks in Mathematics is essential for a good overall percentage in exams. Regular problem-solving practice is key to scoring well in Math exams.NCERT Solutions for Class 6 Maths Chapter 11 PDF Download
NCERT Solutions for Class 6 Maths Chapter 11 Algebra
Algebra is a part of math that uses mathematical expressions to show problems. It is seen as a common link between various math areas and involves using letters like x, y, z, and so on. Class 6 Maths Chapter 11 introduces the basic ideas of Algebra. The NCERT Solutions for Class 6 Maths Chapter 11 Algebra assists students in learning diverse problem-solving methods and reinforcing their basic understanding. The solutions, following the newest CBSE rules, are given step by step by experts in the subject. Exercise 11.1 Page No: 226
1. Find the rule which gives the number of matchsticks required to make the following matchsticks patterns. Use a variable to write the rule.
(a) A pattern of letter T as
Exercise 11.1 Page No: 226
1. Find the rule which gives the number of matchsticks required to make the following matchsticks patterns. Use a variable to write the rule.
(a) A pattern of letter T as
 (b) A pattern of letter Z as
(b) A pattern of letter Z as
 (c) A pattern of letter U as
(c) A pattern of letter U as
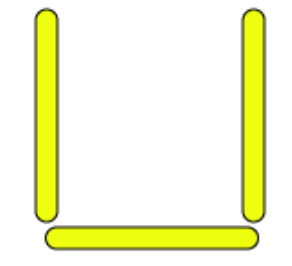 (d) A pattern of letter Vas
(d) A pattern of letter Vas
 (e) A pattern of letter E as
(e) A pattern of letter E as
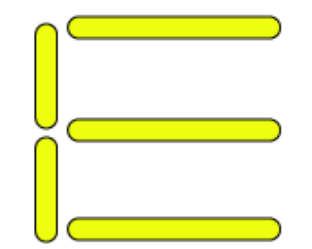 (f) A pattern of letter S as
(f) A pattern of letter S as
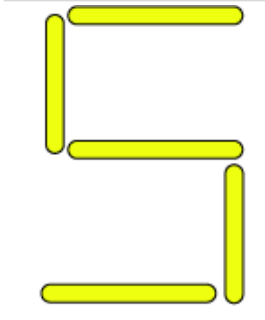 (g) A pattern of letter A as
(g) A pattern of letter A as
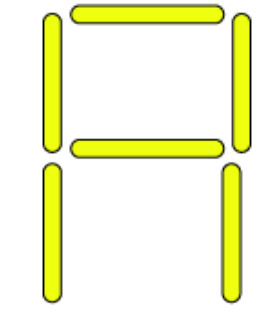 Solutions:
(a)
Solutions:
(a)
 From the figure we observe that two matchsticks are required to make a letter T. Hence, the pattern is 2n
From the figure we observe that two matchsticks are required to make a letter T. Hence, the pattern is 2n
(b)
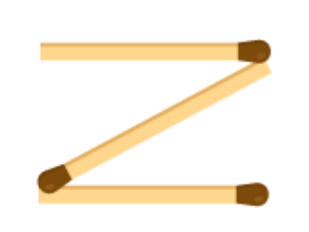 From the figure we observe that three matchsticks are required to make a letter Z. Hence, the pattern is 3n
From the figure we observe that three matchsticks are required to make a letter Z. Hence, the pattern is 3n
(c)
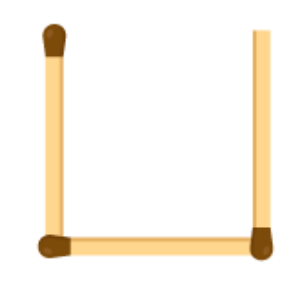 From the figure we observe that three matchsticks are required to make a letter U. Hence, the pattern is 3n
From the figure we observe that three matchsticks are required to make a letter U. Hence, the pattern is 3n
(d)
 From the figure we observe that two matchsticks are required to make a letter V. Hence, the pattern is 2n
From the figure we observe that two matchsticks are required to make a letter V. Hence, the pattern is 2n
(e)
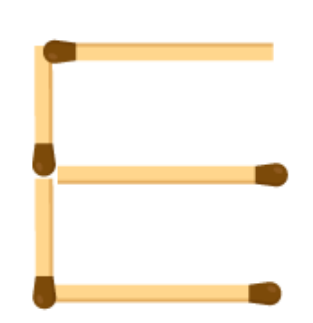 From the figure we observe that 5 matchsticks are required to make a letter E. Hence, the pattern is 5n
From the figure we observe that 5 matchsticks are required to make a letter E. Hence, the pattern is 5n
(f)
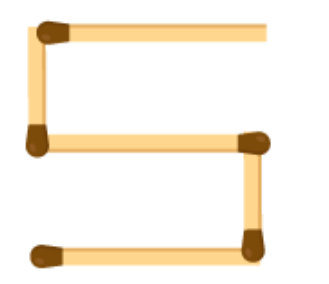 From the figure we observe that 5 matchsticks are required to make a letter S. Hence, the pattern is 5n
From the figure we observe that 5 matchsticks are required to make a letter S. Hence, the pattern is 5n
(g)
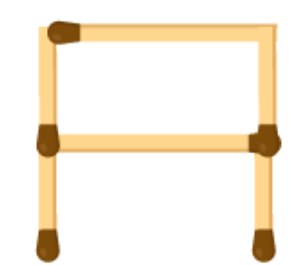 From the figure we observe that 6 matchsticks are required to make a letter A. Hence, the pattern is 6n
From the figure we observe that 6 matchsticks are required to make a letter A. Hence, the pattern is 6n
CBSE Board Exam Centre List 2024
2. We already know the rule for the pattern of letters L, C and F. Some of the letters from Q.1 (given above) give us the same rule as that given by L. Which are these? Why does this happen? Solutions: We know that T requires only two matchsticks. So, the pattern for letter T is 2n. Among all the letters given in question 1, only T and V are the letters which require two matchsticks. Hence, (a) and (d). 3. Cadets are marching in a parade. There are 5 cadets in a row. What is the rule which gives the number of cadets, given the number of rows? (Use n for the number of rows) Solutions: Let n be the number of rows Number of cadets in a row = 5 Total number of cadets = number of cadets in a row × number of rows = 5n 4. If there are 50 mangoes in a box, how will you write the total number of mangoes in terms of the number of boxes? (Use b for the number of boxes.) Solutions: Let b be the number of boxes Number of mangoes in a box = 50 Total number of mangoes = number of mangoes in a box × number of boxes = 50b 5. The teacher distributes 5 pencils per students. Can you tell how many pencils are needed, given the number of students? (Use s for the number of students.) Solutions: Let s be the number of students Pencils given to each student = 5 Total number of pencils = number of pencils given to each student × number of students = 5s 6. A bird flies 1 kilometre in one minute. Can you express the distance covered by the birds in terms of its flying time in minutes? (Use t for flying time in minutes.) Solutions: Let t minutes be the flying time Distance covered in one minute = 1 km Distance covered in t minutes = Distance covered in one minute × Flying time = 1 × t = t km| CBSE Syllabus Class 6 | |
| CBSE Class 6 Science Syllabus | CBSE Class 6 Maths Syllabus |
| CBSE Class 6 Social Science Syllabus | CBSE Class 6 English Syllabus |
 in terms of the number of squares. (Hint: If you remove vertical stick at the end, you will get a pattern of Cs)
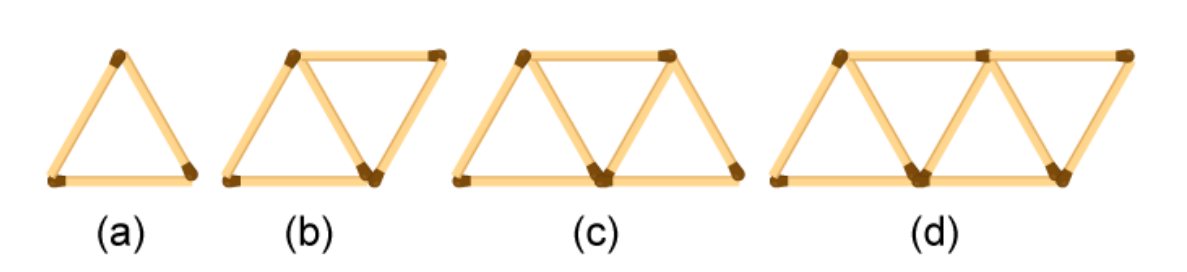
(b) Fig 11.7 gives a matchstick pattern of triangles. As in Exercise 11 (a) above, find the general rule that gives the number of matchsticks in terms of the number of triangles.
in terms of the number of squares. (Hint: If you remove vertical stick at the end, you will get a pattern of Cs)
(b) Fig 11.7 gives a matchstick pattern of triangles. As in Exercise 11 (a) above, find the general rule that gives the number of matchsticks in terms of the number of triangles.
 Solutions:
(a)
We may observe that in the given matchstick pattern, the number of matchsticks are 4, 7, 10 and 13, which is 1 more than the thrice of the number of squares in the pattern
Therefore, the pattern is 3x + 1, where x is the number of squares
(b)
We may observe that in the given matchstick pattern, the number of matchsticks are 3, 5, 7 and 9 which is 1 more than the twice of the number of triangles in the pattern.
Therefore, the pattern is 2x + 1, where x is the number of triangles.
Exercise 11.2 Page No: 230
1. The side of an equilateral triangle is shown by l. Express the perimeter of the equilateral triangle using l.
Solutions:
Side of equilateral triangle = l
Perimeter = l + l + l
= 3l
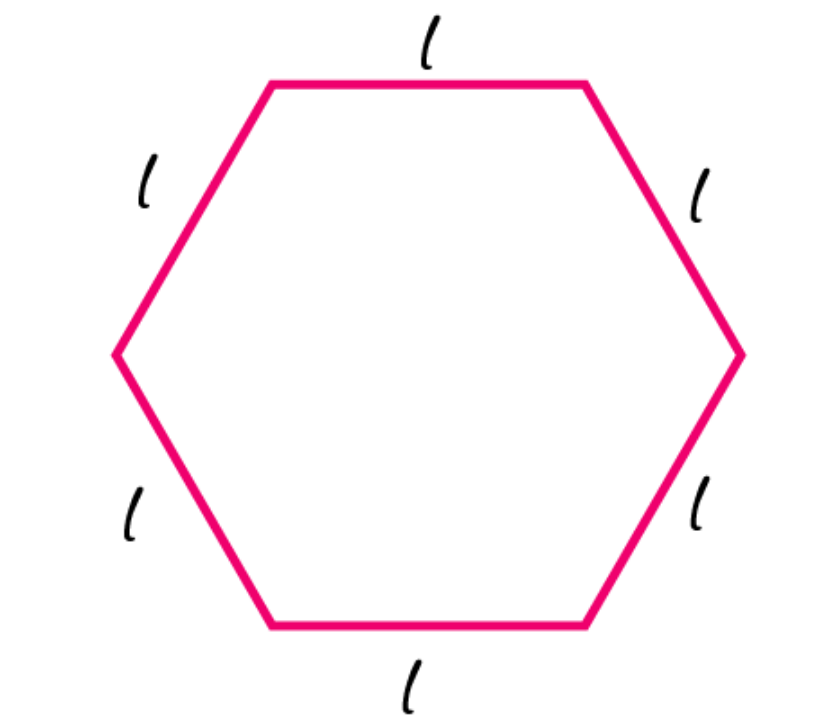
2. The side of the regular hexagon (Fig 11.10) is denoted by l. Express the perimeter of the hexagon using l.
(Hint: A regular hexagon has all its six sides equal in length.)
Solutions:
(a)
We may observe that in the given matchstick pattern, the number of matchsticks are 4, 7, 10 and 13, which is 1 more than the thrice of the number of squares in the pattern
Therefore, the pattern is 3x + 1, where x is the number of squares
(b)
We may observe that in the given matchstick pattern, the number of matchsticks are 3, 5, 7 and 9 which is 1 more than the twice of the number of triangles in the pattern.
Therefore, the pattern is 2x + 1, where x is the number of triangles.
Exercise 11.2 Page No: 230
1. The side of an equilateral triangle is shown by l. Express the perimeter of the equilateral triangle using l.
Solutions:
Side of equilateral triangle = l
Perimeter = l + l + l
= 3l
2. The side of the regular hexagon (Fig 11.10) is denoted by l. Express the perimeter of the hexagon using l.
(Hint: A regular hexagon has all its six sides equal in length.)
 Solutions:
Side of a regular hexagon = l
Perimeter = l + l + l + l + l + 1
= 6l
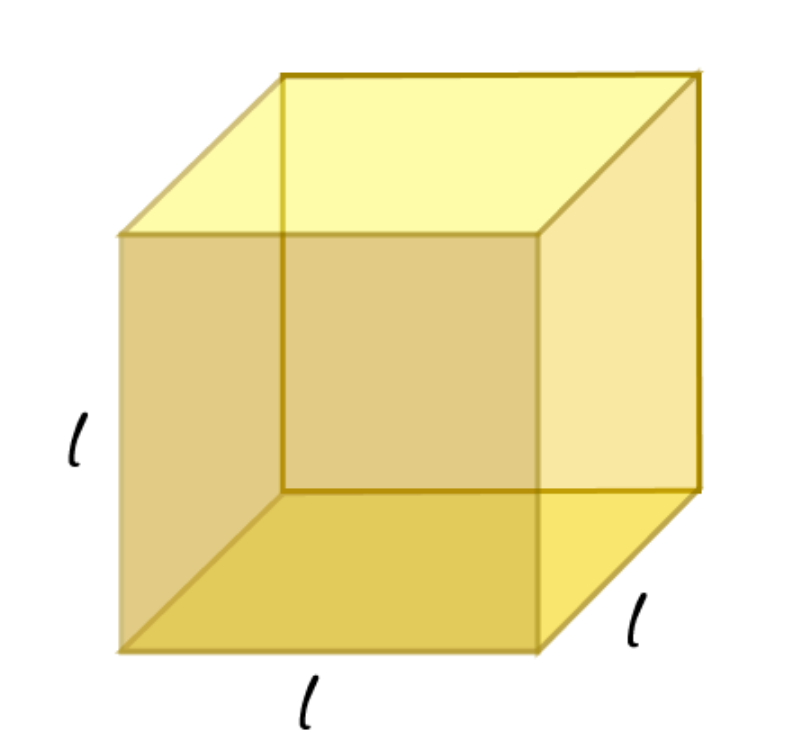
3. A cube is three dimensional figure as shown in Fig 11.11. It has six faces and all of them are identical squares. The length of an edge of the cube is given by l. Find the formula for the total length of the edges of a cube.
Solutions:
Side of a regular hexagon = l
Perimeter = l + l + l + l + l + 1
= 6l
3. A cube is three dimensional figure as shown in Fig 11.11. It has six faces and all of them are identical squares. The length of an edge of the cube is given by l. Find the formula for the total length of the edges of a cube.
 Solutions:
Length of an edge of the cube = l
Number of edges = 12
Total length of the edges = Number of edges × length of an edge
=12l
4. The diameter of a circle is a line which joins two points on the circle and also passes through the centre of the circle. (In the adjoining figure (Fig 11.2) AB is a diameter of a circle; C is its centre.) Express the diameter of the circle (d) in terms of its radius (r).
Solutions:
Length of an edge of the cube = l
Number of edges = 12
Total length of the edges = Number of edges × length of an edge
=12l
4. The diameter of a circle is a line which joins two points on the circle and also passes through the centre of the circle. (In the adjoining figure (Fig 11.2) AB is a diameter of a circle; C is its centre.) Express the diameter of the circle (d) in terms of its radius (r).
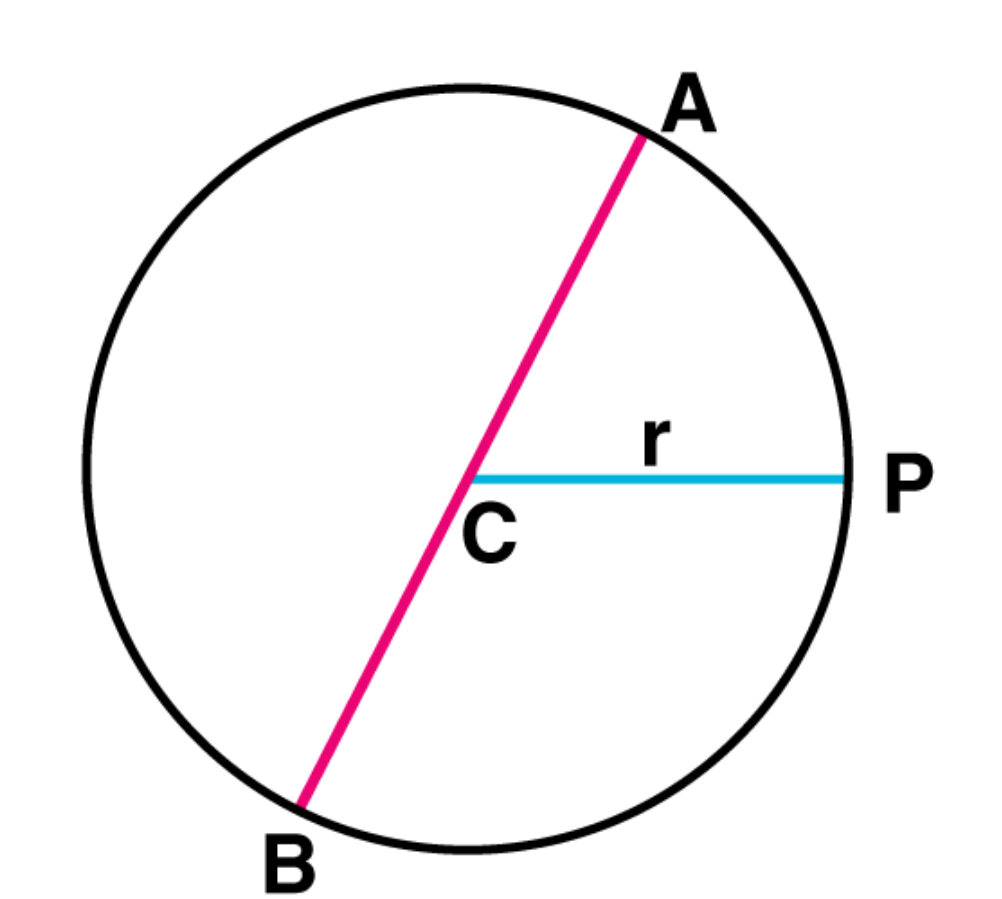 Solutions:
Diameter = AB
= AC + CB
= r + r
= 2r
Hence, the diameter of the circle in terms of its radius is 2r
5. To find sum of three numbers 14, 27 and 13 we can have two ways:
(a) We may first add 14 and 27 to get 41and then add 13 to it to get the total sum 54 or
(b) We may add 27 and 13 to get 40 and then add 14 to get the sum 54. Thus, (14 + 27) + 13 = 14 + (27 + 13)
Solutions:
For any three whole numbers a, b and c
(a + b) + c = a + (b + c)
Exercise 11.3 Page No: 233
1. Make up as many expressions with numbers (no variables) as you can from three numbers 5, 7 and 8. Every number should be used not more than once. Use only addition, subtraction and multiplication.
Solutions:
Some of the expressions formed by 5, 7 and 8 are as follows
5 × (8 – 7)
5 × (8 + 7)
(8 + 5) × 7
(8 – 5) × 7
(7 + 5) × 8
(7 – 5) × 8
2. Which out of the following are expressions with numbers only?
(a) y + 3
(b) 5 (21 – 7) + 7 × 2
(c) (7 × 20) – 8z
(d) 5
(e) 5 – 5n
(f) 3x
(g) (7 × 20) – (5 × 10) – 45 + p
Solutions:
(c)
and
(d)
are the expressions with numbers only.
Solutions:
Diameter = AB
= AC + CB
= r + r
= 2r
Hence, the diameter of the circle in terms of its radius is 2r
5. To find sum of three numbers 14, 27 and 13 we can have two ways:
(a) We may first add 14 and 27 to get 41and then add 13 to it to get the total sum 54 or
(b) We may add 27 and 13 to get 40 and then add 14 to get the sum 54. Thus, (14 + 27) + 13 = 14 + (27 + 13)
Solutions:
For any three whole numbers a, b and c
(a + b) + c = a + (b + c)
Exercise 11.3 Page No: 233
1. Make up as many expressions with numbers (no variables) as you can from three numbers 5, 7 and 8. Every number should be used not more than once. Use only addition, subtraction and multiplication.
Solutions:
Some of the expressions formed by 5, 7 and 8 are as follows
5 × (8 – 7)
5 × (8 + 7)
(8 + 5) × 7
(8 – 5) × 7
(7 + 5) × 8
(7 – 5) × 8
2. Which out of the following are expressions with numbers only?
(a) y + 3
(b) 5 (21 – 7) + 7 × 2
(c) (7 × 20) – 8z
(d) 5
(e) 5 – 5n
(f) 3x
(g) (7 × 20) – (5 × 10) – 45 + p
Solutions:
(c)
and
(d)
are the expressions with numbers only.
| Related Links |
 Solutions:
(a)
(i)
Sarita’s age after 5 years from now = Sarita’s present age + 5
= (y + 5) years
(ii)
Sarita’s age 3 years back = Sarita’s present age – 3
= (y – 3) years
(iii)
Grandfather’s age = 6 × Sarita’s present age
= 6y years
(iv)
Grandmother’s age = grandfather’s present age – 2
= (6y -2) years
(v)
Father’s age = 5 + 3 × Sarita’s present age
= (5 + 3y) years
(b)
Length = 3 × Breadth – 4
l = (3b – 4) metres
(c)
Length = 5 × Breadth
l = 5h cm
Breadth = 5 × length – 10
b = (5h – 10) cm
(d)
The step at which Beena is = (step at which Meena is) + 8
= (s + 8)
The step at which Leena is = (step at which Meena is) – 7
= (s – 7)
Total steps = 4 × (step at which Meena is) – 10
= (4s – 10)
(e)
Speed = v km / hr
Distance travelled in 5 hours = 5 × v
= 5v km
Total distance travelled between Daspur and Beespur = (5v + 20) km
Solutions:
(a)
(i)
Sarita’s age after 5 years from now = Sarita’s present age + 5
= (y + 5) years
(ii)
Sarita’s age 3 years back = Sarita’s present age – 3
= (y – 3) years
(iii)
Grandfather’s age = 6 × Sarita’s present age
= 6y years
(iv)
Grandmother’s age = grandfather’s present age – 2
= (6y -2) years
(v)
Father’s age = 5 + 3 × Sarita’s present age
= (5 + 3y) years
(b)
Length = 3 × Breadth – 4
l = (3b – 4) metres
(c)
Length = 5 × Breadth
l = 5h cm
Breadth = 5 × length – 10
b = (5h – 10) cm
(d)
The step at which Beena is = (step at which Meena is) + 8
= (s + 8)
The step at which Leena is = (step at which Meena is) – 7
= (s – 7)
Total steps = 4 × (step at which Meena is) – 10
= (4s – 10)
(e)
Speed = v km / hr
Distance travelled in 5 hours = 5 × v
= 5v km
Total distance travelled between Daspur and Beespur = (5v + 20) km
NCERT Solutions for Class 6 Maths Chapter 11 FAQs
What is Algebra? What is a Variable?
Algebra is a branch of mathematics that deals with symbols and the rules for manipulating those symbols. A variable is a symbol used to represent an unknown or arbitrary number in mathematical expressions.
Is Chapter 11 Class 6 Algebra Easy?
The difficulty of Chapter 11 in Class 6 Algebra varies from person to person. Practice and understanding the concepts will make it easier.
How do you solve Chapter 11 Algebra in Class 6?
Solve Class 6 Algebra Chapter 11 by understanding the basic concepts, practicing regularly, and seeking help when needed from teachers or classmates.
How to score good marks in Class 6 Maths Algebra?
To score well in Class 6 Maths Algebra, focus on understanding concepts, regular practice, solving problems, and seeking help when faced with challenges.
How can I download the Solutions for NCERT Class 6 Math Chapter 11?
Solutions for NCERT Class 6 Math Chapter 11 can be downloaded from reputable educational websites or by referring to official NCERT sources.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App







