NCERT Solutions for Class 6 Maths Chapter 10 Mensuration PDF
NCERT Solutions for Class 6 Maths Chapter 10 have been provided below for the reference of CBSE Class 6 students. Students can check the complete NCERT solutions for Maths Chapter 10 on this page
Jasdeep Bhatia12 Jan, 2024
Share
NCERT Solutions for Class 6 Maths Chapter 10
NCERT Solutions for Class 6 Maths Chapter 10: NCERT Solutions for Class 6 Maths Chapter 10, Mensuration, is a valuable tool for students preparing to learn about Mensuration. This Bchapter holds significant importance in Class 6 Maths, with numerous questions appearing in yearly exams, making it a key part of the subject. Using the NCERT Solutions for Class 6 Maths can aid students in grasping the concepts more effectively. Mathematics is a subject where scoring well is crucial. Achieving high marks in this subject can greatly boost students' overall grades. To support students in attaining the highest marks in exams, the experts at PhysicsWallah’s have developed these NCERT Solutions in line with the latest CBSE guidelines. Students can access these solutions online or offline at any time and from anywhere.NCERT Solutions for Class 6 Maths Chapter 10 PDF Download
NCERT Solutions for Class 6 Maths Chapter 10 Mensuration
NCERT Solutions for Class 6 Maths Chapter 10 Mensuration focus on giving information and getting students ready by presenting various ways to solve questions. As Mathematics is a subject where scoring is important, enhancing performance in this subject can significantly boost the overall score of students. For subjects such as Science, Maths, English, and Hindi, students can refer to NCERT Solutions . Exercise 10.1 Page No. 212 1. Find the perimeter of each of the following figures: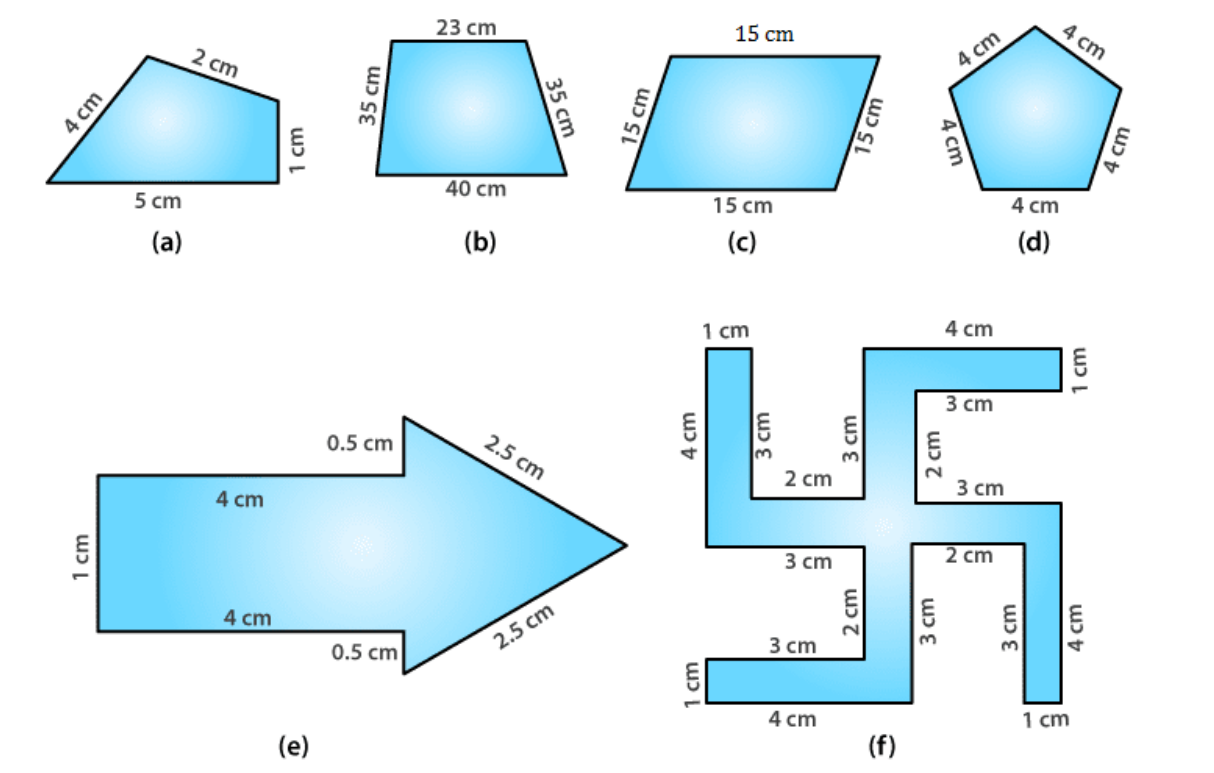
Solutions:
(a)
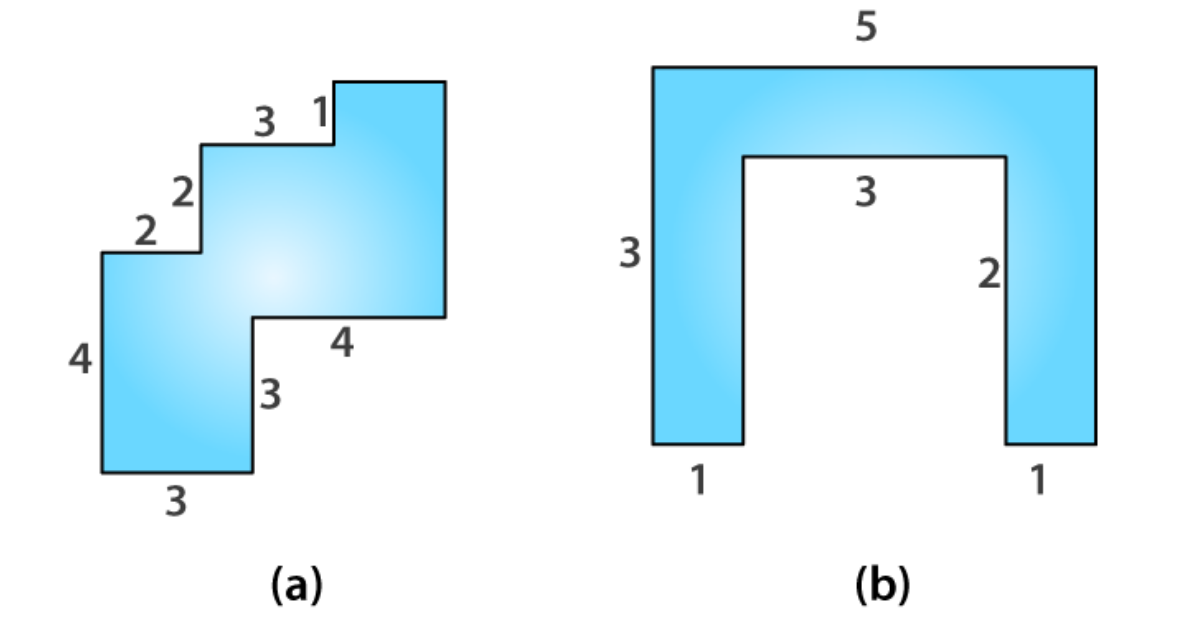
Perimeter = Sum of all the sides
= 1 + 2 + 4 + 5
= 12 cm
(b)
Perimeter = Sum of all the sides
= 23 + 35 + 35 + 40
= 133 cm
(c)
Perimeter = Sum of all the sides
= 15 + 15 + 15 + 15
= 60 cm
(d)
Perimeter = Sum of all the sides
= 4 + 4 + 4 + 4 + 4
=20 cm
(e)
Perimeter = Sum of all the sides
= 1 + 4 + 0.5 + 2.5 + 2.5 + 0.5 + 4
= 15 cm
(f)
Perimeter = Sum of all the sides
= 4 + 1 + 3 + 2 + 3 + 4 + 1 + 3 + 2 + 3 + 4 + 1 + 3 + 2 + 3 + 4 + 1 + 3 + 2 + 3
= 52 cm
2. The lid of a rectangular box, with sides 40 cm by 10 cm, is sealed all around with tape. What is the length of the tape required?
Solutions:
Length of required tape = Perimeter of rectangle
= 2 (Length + Breadth)
= 2 (40 + 10)
= 2 (50)
= 100 cm
∴ The required length of tape is 100 cm.
3. A table top measures 2 m 25 cm by 1 m 50 cm. What is the perimeter of the tabletop?
Solutions:
Length of tabletop = 2 m 25 cm = 2.25 m
Breadth of tabletop = 1 m 50 cm = 1.50 m
Perimeter of tabletop = 2 (Length + Breadth)
= 2 (2.25 + 1.50)
= 2 (3.75)
= 2 × 3.75
= 7.5 m
∴ The perimeter of the table top is 7.5 m.
4. What is the length of the wooden strip required to frame a photograph of length and breadth, 32 cm and 21 cm, respectively?
Solutions:
The required length of the wooden strip = Perimeter of the photograph
= 2 (Length + Breadth)
= 2 (32 + 21)
= 2 (53)
= 2 × 53
= 106 cm
∴ The required length of the wooden strip is 106 cm.
5. A rectangular piece of land measures 0.7 km by 0.5 km. Each side is to be fenced with 4 rows of wires. What is the length of the wire needed?
Solutions:
Perimeter of the field = 2 (Length + Breadth)
= 2 (0.7 + 0.5)
= 2 (1.2)
= 2 × 1.2
= 2.4 km
Each side is to be fenced with 4 rows = 4 × 2.4
= 9.6 km
∴ The total length of the required wire is 9.6 km.
6. Find the perimeter of each of the following shapes:
(a) A triangle of sides 3 cm, 4 cm and 5 cm
(b) An equilateral triangle of side 9 cm
(c) An isosceles triangle with equal sides of 8 cm each and the third side of 6 cm.
Solutions:
(a)
Perimeter of triangle = 3 + 4 + 5
= 12 cm
(b)
Perimeter of an equilateral triangle = 3 × side
= 3 × 9
= 27 cm
(c)
Perimeter of isosceles triangle = 8 + 8 + 6
= 22 cm
7. Find the perimeter of a triangle with sides measuring 10 cm, 14 cm and 15 cm.
Solutions:
Perimeter of triangle = 10 + 14 + 15
= 39 cm
∴ The perimeter of the triangle is 39 cm.
8. Find the perimeter of a regular hexagon with each side measuring 8 m.
Solutions:
Perimeter of hexagon = 6 × 8
= 48 m
∴ The perimeter of the regular hexagon is 48 m.
9. Find the side of the square whose perimeter is 20 m.
Solutions:
Perimeter of square = 4 × side
20 = 4 × side
Side = 20 / 4
Side = 5 m
∴ The side of the square is 5 m.
10. The perimeter of a regular pentagon is 100 cm. How long is its each side?
Solutions:
The perimeter of the regular pentagon = 100 cm
5 × side = 100 cm
Side = 100 / 5
Side = 20 cm
∴ The side of the pentagon is 20 cm.
11. A piece of string is 30 cm long. What will be the length of each side if the string is used to form:
(a) a square?
(b) an equilateral triangle?
(c) a regular hexagon?
Solutions:
(a)
Perimeter of square = 30 cm
4 × side = 30
Side = 30 / 4
Side = 7.5 cm
(b)
Perimeter of equilateral triangle = 30 cm
3 × side = 30
Side = 30 / 3
Side = 10 cm
(c)
Perimeter of regular hexagon = 30 cm
6 × side = 30
Side = 30 / 6
Side = 5 cm
12. Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is its third side?
Solutions:
Let x cm be the third side
Perimeter of triangle = 36 cm
12 + 14 + x = 36
26 + x = 36
x = 36 – 26
x = 10 cm
∴ The third side is 10 cm.
13. Find the cost of fencing a square park of side 250 m at the rate of ₹ 20 per metre.
Solutions:
Side of square = 250 m
Perimeter of square = 4 × side
= 4 × 250
= 1000 m
Cost of fencing = ₹ 20 per m
Cost of fencing for 1000 m = ₹ 20 × 1000
= ₹ 20,000
∴ The cost of fencing the square park is ₹ 20,000.
14. Find the cost of fencing a rectangular park of length 175 cm and breadth 125 m at the rate of ₹ 12 per metre.
Solutions:
Length = 175 cm
Breadth = 125 m
Perimeter of rectangular park = 2 (Length + Breadth)
= 2 (175 + 125)
= 2 (300)
= 2 × 300
= 600 m
Cost of fencing = 12 × 600
= 7200
∴ The cost of fencing is ₹ 7,200.
15. Sweety runs around a square park of side 75 m. Bulbul runs around a rectangular park with a length of 60 m and a breadth of 45 m. Who covers less distance?
Solutions:
Perimeter of square = 4 × side
= 4 × 75
= 300 m
∴ The distance covered by Sweety is 300 m
Perimeter of the rectangular park = 2 (Length + Breadth)
= 2 (60 + 45)
= 2 (105)
= 2
×
105
= 210 m
∴ The distance covered by Bulbul is 210 m
Hence, Bulbul covers less distance than Sweety.
16. What is the perimeter of each of the following figures? What do you infer from the answers?
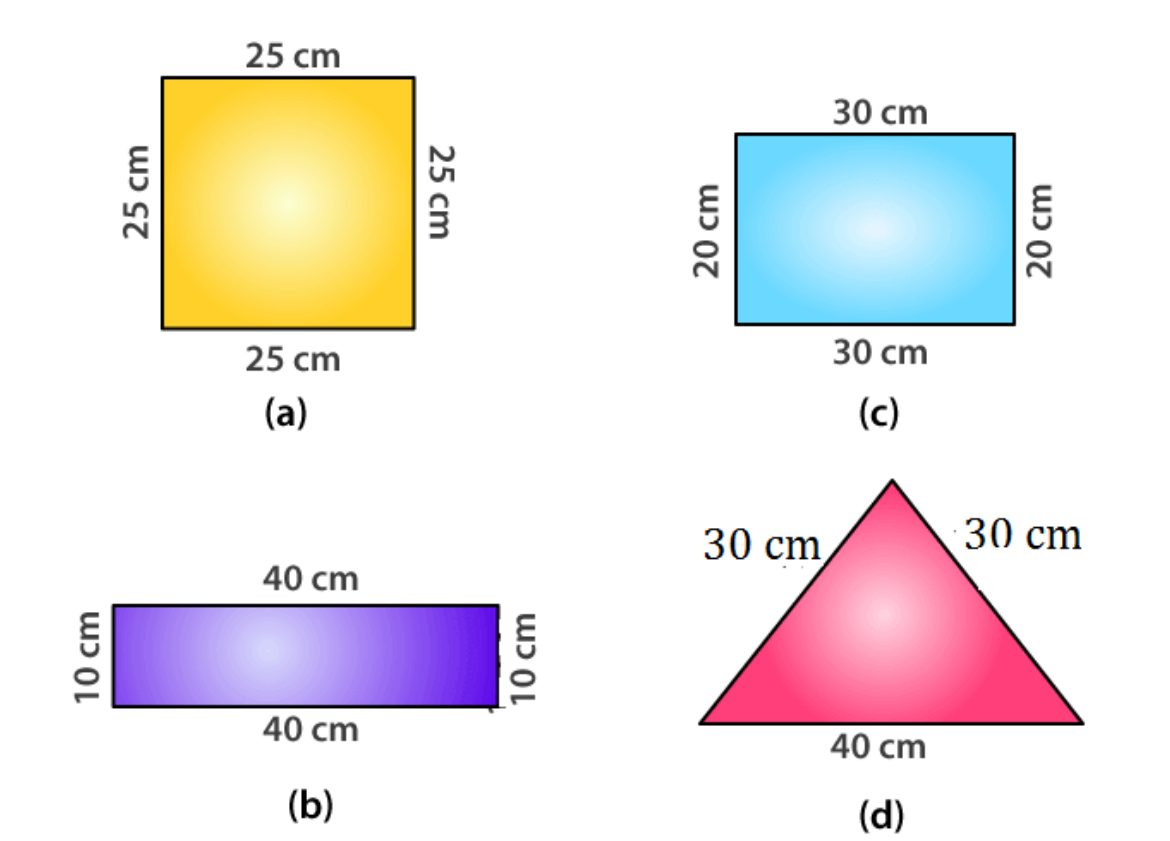Solutions:
(a)
Perimeter of square = 4 × side
= 4 × 25
= 100 cm
(b)
Perimeter of rectangle = 2 (40 + 10)
= 2 × 50
= 100 cm
(c)
Perimeter of rectangle = 2 (Length + Breadth)
= 2 (30 + 20)
= 2 (50)
= 2 × 50
= 100 cm
(d)
Perimeter of triangle = 30 + 30 + 40
= 100 cm
∴ All the figures have the same perimeter.
17. Avneet buys 9 square paving slabs, each with a side of 1 / 2 m. He lays them in the form of a square.
(a) What is the perimeter of his arrangement [fig 10.7(i)]?
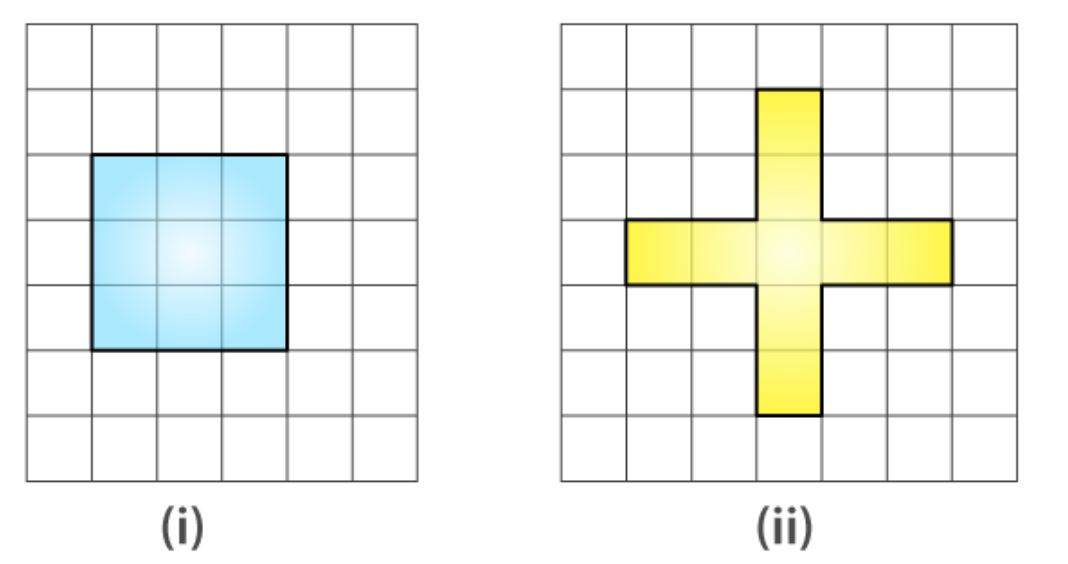(b) Shari does not like his arrangement. She gets him to lay them out like a cross. What is the perimeter of her arrangement [(Fig 10.7 (ii)]?
(c) Which has a greater perimeter?
(d) Avneet wonders if there is a way of getting an even greater perimeter. Can you find a way of doing this? (The paving slabs must meet along complete edges, i.e. they cannot be broken.)
Solutions:
(a)
Side of square = 3 × side
= 3 × 1 / 2
= 3 / 2 m
Perimeter of Square = 4 × 3 / 2
= 2 × 3
= 6 m
(b)
Perimeter = 0.5 + 1 + 1 + 0.5 + 1 + 1 + 0.5 + 1 + 1 + 0.5 + 1 + 1
= 10 m
(c)
The arrangement in the form of a cross has a greater perimeter.
(d)
Perimeters greater than 10 m cannot be determined.
Exercise 10.2 Page No. 216
1. Find the areas of the following figures by counting squares:
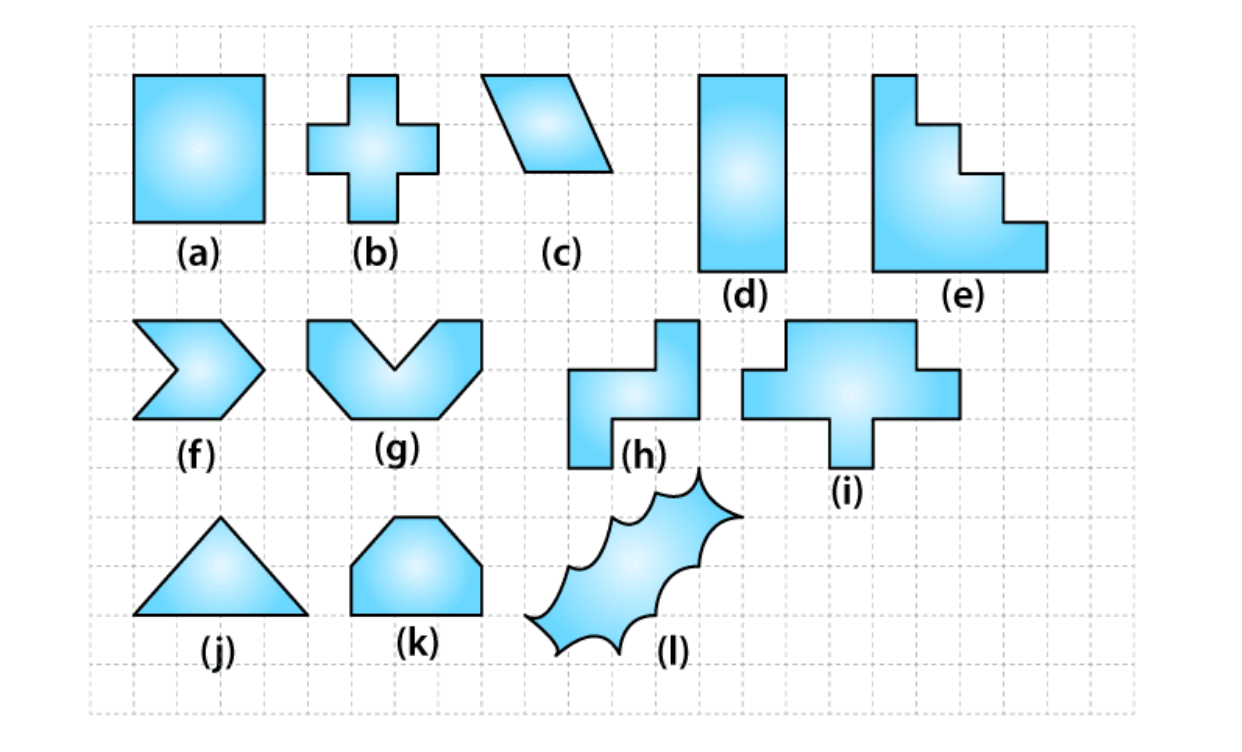
(a)
The figure contains only 9 fully filled squares. Hence, the area of this figure will be 9 square units.
(b)
The figure contains only 5 fully filled squares. Hence, the area of this figure will be 5 square units.
(c)
The figure contains 2 fully filled squares and 4 half filled squares. Hence, the area of this figure will be 4 square units.
(d)
The figure contains only 8 fully filled squares. Hence, the area of this figure will be 8 square units.
(e)
The figure contains only 10 fully filled squares. Hence, the area of this figure will be 10 square units.
(f)
The figure contains only 2 fully filled squares and 4 half filled squares. Hence, the area of this figure will be 4 square units.
(g)
The figure contains 4 fully filled squares and 4 half filled squares. Hence, the area of this figure will be 6 square units.
(h)
The figure contains 5 fully filled squares. Hence, the area of this figure will be 5 square units.
(i)
The figure contains 9 fully filled squares. Hence, the area of this figure will be 9 square units.
(j)
The figure contains 2 fully filled squares and 4 half filled squares. Hence, the area of this figure will be 4 square units.
(k)
The figure contains 4 fully filled squares and 2 half filled squares. Hence, the area of this figure will be 5 square units.
(l)
From the given figure, we observe
| Covered Area | Number | Area Estimate (square units) |
| Fully filled squares | 2 | 2 |
| Half filled squares | – | – |
| More than half filled squares | 6 | 6 |
| Less than half filled squares | 6 | 0 |
| Covered Area | Number | Area Estimate (square units) |
| Fully filled squares | 5 | 5 |
| Half filled squares | – | – |
| More than half filled squares | 9 | 9 |
| Less than half filled squares | 12 | 0 |
| Covered Area | Number | Area estimate (square units) |
| Fully filled squares | 8 | 8 |
| Half filled squares | – | – |
| More than half filled squares | 10 | 10 |
| Less than half filled squares | 9 | 0 |
CBSE Board Exam Centre List 2024
Exercise 10.3 Page No. 219 1. Find the area of the rectangles whose sides are: (a) 3 cm and 4 cm (b) 12 m and 21 m (c) 2 km and 3 km (d) 2 m and 70 cm Solutions: We know that Area of rectangle = Length × Breadth (a) l = 3 cm and b = 4 cm Area = l × b = 3 × 4 = 12 cm 2 (b) l = 12 m and b = 21 m Area = l × b = 12 × 21 = 252 m 2 (c) l = 2 km and b = 3 km Area = l × b = 2 × 3 = 6 km 2 (d) l = 2 m and b = 70 cm = 0.70 m Area = l × b = 2 × 0.70 = 1.40 m 2 2. Find the areas of the squares whose sides are: (a) 10 cm (b) 14 cm (c) 5 m Solutions: (a) Area of square = side 2 = 10 2 = 100 cm 2 (b) Area of square = side 2 = 14 2 = 196 cm 2 (c) Area of square = side 2 = 5 2 =25 cm 2 3. The length and breadth of the three rectangles are as given below: (a) 9 m and 6 m (b) 17 m and 3 m (c) 4 m and 14 m Which one has the largest area, and which one has the smallest? Solutions: (a) Area of rectangle = l × b = 9 × 6 = 54 m 2 (b) Area of rectangle = l × b = 17 × 3 = 51 m 2 (c) Area of rectangle = l × b = 4 × 14 = 56 m 2 The area of rectangle 56 m 2 , i.e. (c), is the largest area and the area of rectangle 51 m 2 , i.e. (b), is the smallest area 4. The area of a rectangular garden 50 m long is 300 sq. m. Find the width of the garden. Solutions: Area of rectangle = length × width 300 = 50 × width width = 300 / 50 width = 6 m ∴ The width of the garden is 6 m. 5. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹ 8 per hundred sq. m? Solutions: Area of land = length × breadth = 500 × 200 = 1,00,000 m 2 ∴ Cost of tiling 1,00,000 sq. m of land = (8 × 1,00,000) / 100 = ₹ 8000 ∴ The cost of tiling a rectangular plot of land is ₹ 8000.| CBSE Syllabus Class 6 | |
| CBSE Class 6 Science Syllabus | CBSE Class 6 Maths Syllabus |
| CBSE Class 6 Social Science Syllabus | CBSE Class 6 English Syllabus |
| Related Links |
Solutions:
(a)
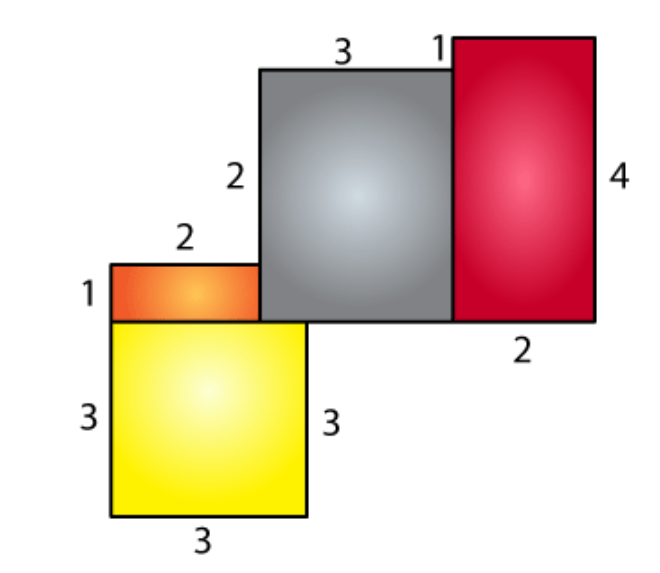Area of yellow region = 3 × 3
= 9 cm
2
Area of orange region = 1× 2
= 2 cm
2
Area of grey region = 3 × 3
= 9 cm
2
Area of brown region = 2 × 4
= 8 cm
2
Total area = 9 + 2 + 9 + 8
= 28 cm
2
∴ The total area is 28 cm
2
.
(b)
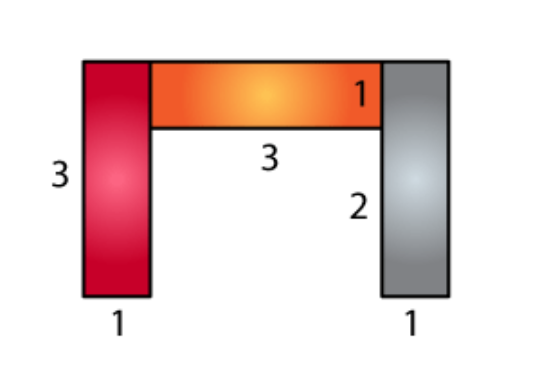Area of brown region = 3 × 1
= 3 cm
2
Area of orange region = 3 × 1
= 3 cm
2
Area of grey region = 3 × 1
= 3 cm
2
Total area = 3 + 3 + 3
= 9 cm
2
∴ The total area is 9 cm
2
.
NCERT Solutions for Class 6 Maths Chapter 10 FAQs
How do you calculate the perimeter of a square with a side length of 3 cm?
The perimeter of a square with a side length of 3 cm is calculated by multiplying the length of one side by the number of sides, i.e., 3 cm x 4 sides = 12 cm.
What does the term "tangent" refer to in relation to a circle?
In geometry, the tangent of a circle is a straight line that touches the circle at a single point, without crossing through it.
Is NCERT Class 6 Maths Chapter 10 considered easy?
The difficulty of NCERT Class 6 Maths Chapter 10 varies for each student depending on individual understanding and practice.
What is the difference between a minor arc and a major arc in a circle?
A minor arc is a portion of a circle's circumference, while a major arc is the longer portion that includes more than half of the circle's circumference.
How can one achieve good marks in Class 6 Maths Chapter 10?
To excel in Class 6 Maths Chapter 10, focus on understanding concepts, practice regularly, and seek clarification on doubts from teachers or classmates.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App