Ray Optics and Optical Instruments NCERT Solutions are highly useful for students preparing for the Class 12 Physics board examination.
With the CBSE Class 12 Physics exam scheduled on 20th February 2026, this chapter becomes a must-revise topic due to its high weightage and scoring numericals. Ray Optics carries around 10 marks, making it an important contributor to the overall 80-mark theory paper.
As the board exams are approaching, focused practice and strong conceptual clarity are essential to avoid mistakes in numericals and ray diagrams. NCERT Solutions class 12 Chapter 9 Ray Optics and Optical Instruments help students revise efficiently by providing step-by-step solutions, accurate ray diagrams, and well-structured, exam-oriented answers aligned with the CBSE marking scheme.
Ray Optics NCERT Solutions for Class 12 Physics
Ray Optics NCERT Solutions are given here to help students understand reflection, refraction, total internal reflection, and optical instruments easily.
The solutions explain each concept clearly and focus on formula application, numerical problem-solving, and diagram-based answers, which are frequently asked in board exams. These solutions are especially useful for last-minute revision, helping students avoid common mistakes and improve speed and accuracy.
Physics Chapter 9 Ray Optics and Optical Instruments
NCERT Solutions for Chapter 9 Ray Optics and Optical Instruments provide complete coverage of all textbook questions, including derivations, ray diagrams, and numericals. Each solution follows the CBSE marking scheme, helping students understand how to present answers correctly to score full marks.
Class 12 Ray Optics and Optical Instruments NCERT Solutions (All Exercises)
Here are the questions along with the answers given at the end of the chapter. Students must understand each numerical and practice them thoroughly for CBSE Class 12th Physics Board exam:
Question 1. A small candle, 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?Solution : Size of the candle, h= 2.5 cm Image size = h’ Object distance, u= −27 cm Radius of curvature of the concave mirror, R= −36 cm Focal length of the concave mirror,
Image distance = v The image distance can be obtained using the mirror formula:
Therefore, the screen should be placed 54 cm away from the mirror to obtain a sharp image. The magnification of the image is given as:
The height of the candle’s image is 5 cm. The negative sign indicates that the image is inverted and real. If the candle is moved closer to the mirror, then the screen will have to be moved away from the mirror in order to obtain the image.
Question 2. A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of the image and the magnification. Describe what happens as the needle is moved farther from the mirror.
Solution : Height of the needle, h1 = 4.5 cm Object distance, u = −12 cm Focal length of the convex mirror, f = 15 cm Image distance = v The value of v can be obtained using the mirror formula:
Hence, the image of the needle is 6.7 cm away from the mirror. Also, it is on the other side of the mirror. The image size is given by the magnification formula:
Hence, magnification of the image,
The height of the image is 2.5 cm. The positive sign indicates that the image is erect, virtual, and diminished. If the needle is moved farther from the mirror, the image will also move away from the mirror, and the size of the image will reduce gradually.
Question 3. A tank is filled with water to a height of 12.5 cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be 9.4 cm. What is the refractive index of water? If water is replaced by a liquid of refractive index 1.63 up to the same height, by what distance would the microscope have to be moved to focus on the needle again?
Solution : Actual depth of the needle in water, h1 = 12.5 cm Apparent depth of the needle in water, h2 = 9.4 cm Refractive index of water = μ The value of μcan be obtained as follows:
Hence, the refractive index of water is about 1.33. Water is replaced by a liquid of refractive index,
The actual depth of the needle remains the same, but its apparent depth changes. Let y be the new apparent depth of the needle. Hence, we can write the relation:
Hence, the new apparent depth of the needle is 7.67 cm. It is less than h2. Therefore, to focus the needle again, the microscope should be moved up. ∴Distance by which the microscope should be moved up = 9.4 − 7.67 = 1.73 cm
Question 4. Figures 9.27(a) and (b) show refraction of a ray in air incident at 60° with the normal to a glass-air and water-air interface, respectively. Predict the angle of refraction in glass when the angle of incidence in water is 45° with the normal to a water-glass interface [Fig. 9.27(c)]
Solution : As per the given figure, for the glass − air interface: Angle of incidence, i = 60° Angle of refraction, r = 35° The relative refractive index of glass with respect to air is given by Snell’s law as:
As per the given figure, for the air − water interface: Angle of incidence, i = 60° Angle of refraction, r = 47° The relative refractive index of water with respect to air is given by Snell’s law as:
Using (1) and (2), the relative refractive index of glass with respect to water can be obtained as:
The following figure shows the situation involving the glass − water interface.
Angle of incidence, i = 45° Angle of refraction = r From Snell’s law, r can be calculated as:
Hence, the angle of refraction at the water − glass interface is 38.68°.
Question 5. A small bulb is placed at the bottom of a tank containing water to a depth of 80 cm. What is the area of the surface of water through which light from the bulb can emerge out? Refractive index of water is 1.33. (Consider the bulb to be a point source.)
Solution : Actual depth of the bulb in water, d1 = 80 cm = 0.8 m Refractive index of water,
The given situation is shown in the following figure:
Where, i = Angle of incidence r = Angle of refraction = 90° Since the bulb is a point source, the emergent light can be considered as a circle of radius,
Using Snell’ law, we can write the relation for the refractive index of water as:
Using the given figure, we have the relation:
∴R = tan 48.75° × 0.8 = 0.91 m ∴Area of the surface of water = πR2 = π (0.91)2 = 2.61 m2 Hence, the area of the surface of water through which the light from the bulb can emerge is approximately 2.61 m2.
Question 6. A prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation is measured to be 40°. What is the refractive index of the material of the prism? The refracting angle of the prism is 60°. If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light.
Solution : Angle of minimum deviation,
= 40° Angle of the prism, A = 60° Refractive index of water, µ = 1.33 Refractive index of the material of the prism = 
The angle of deviation is related to refractive index
as: 
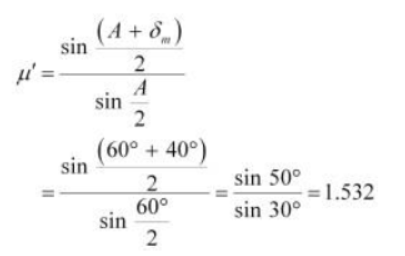
Hence, the refractive index of the material of the prism is 1.532. Since the prism is placed in water, let
be the new angle of minimum deviation for the same prism. The refractive index of glass with respect to water is given by the relation:
Hence, the new minimum angle of deviation is 10.32°.
Question 7. Double-convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length is to be 20 cm?
Solution : Refractive index of glass,
Focal length of the double-convex lens, f = 20 cm Radius of curvature of one face of the lens = R1 Radius of curvature of the other face of the lens = R2 Radius of curvature of the double-convex lens = R
The value of R can be calculated as:
Hence, the radius of curvature of the double-convex lens is 22 cm.
Question 8. A beam of light converges at a point P. Now a lens is placed in the path of the convergent beam 12 cm from P. At what point does the beam converge if the lens is (a) a convex lens of focal length 20 cm, and (b) a concave lens of focal length 16 cm?
Solution : In the given situation, the object is virtual and the image formed is real. Object distance, u = +12 cm (a) Focal length of the convex lens, f = 20 cm Image distance = v According to the lens formula, we have the relation:
Hence, the image is formed 7.5 cm away from the lens, toward its right. (b) Focal length of the concave lens, f = −16 cm Image distance = v According to the lens formula, we have the relation:
Hence, the image is formed 48 cm away from the lens, toward its right.
Question 9. An object of size 3.0 cm is placed 14 cm in front of a concave lens of focal length 21 cm. Describe the image produced by the lens. What happens if the object is moved further away from the lens?
Solution : Size of the object, h1 = 3 cm Object distance, u = −14 cm Focal length of the concave lens, f = −21 cm Image distance = v According to the lens formula, we have the relation:
Hence, the image is formed on the other side of the lens, 8.4 cm away from it. The negative sign shows that the image is erect and virtual. The magnification of the image is given as:
Hence, the height of the image is 1.8 cm. If the object is moved further away from the lens, then the virtual image will move toward the focus of the lens, but not beyond it. The size of the image will decrease with the increase in the object distance.
Question 10. What is the focal length of a convex lens of focal length 30 cm in contact with a concave lens of focal length 20 cm? Is the system a converging or a diverging lens? Ignore thickness of the lenses.
Solution : Focal length of the convex lens, f1 = 30 cm Focal length of the concave lens, f2 = −20 cm Focal length of the system of lenses = f
The equivalent focal length of a system of two lenses in contact is given as:
Hence, the focal length of the combination of lenses is 60 cm. The negative sign indicates that the system of lenses acts as a diverging lens.
Question 11. A compound microscope consists of an objective lens of focal length 2.0 cm and an eyepiece of focal length 6.25 cm separated by a distance of 15 cm. How far from the objective should an object be placed in order to obtain the final image at (a) the least distance of distinct vision (25 cm), and (b) at infinity? What is the magnifying power of the microscope in each case?
Solution : Focal length of the objective lens, f1 = 2.0 cm Focal length of the eyepiece, f2 = 6.25 cm Distance between the objective lens and the eyepiece, d = 15 cm (a) Least distance of distinct vision,
∴Image distance for the eyepiece, v2 = −25 cm Object distance for the eyepiece = u2 According to the lens formula, we have the relation:
Image distance for the objective lens,
Object distance for the objective lens = u1 According to the lens formula, we have the relation:
Magnitude of the object distance,
The magnifying power of a compound microscope is given by the relation:
Hence, the magnifying power of the microscope is 20.
(b) The final image is formed at infinity. ∴Image distance for the eyepiece,
Object distance for the eyepiece = u2 According to the lens formula, we have the relation: 
Image distance for the objective lens,
Object distance for the objective lens = u1 According to the lens formula, we have the relation: 
Magnitude of the object distance, 
= 2.59 cm The magnifying power of a compound microscope is given by the relation:
Hence, the magnifying power of the microscope is 13.51.
Question 12. A person with a normal near point (25 cm) using a compound microscope with objective of focal length 8.0 mm and an eyepiece of focal length 2.5 cm can bring an object placed at 9.0 mm from the objective in sharp focus. What is the separation between the two lenses? Calculate the magnifying power of the microscope,
Solution : Focal length of the objective lens, fo = 8 mm = 0.8 cm Focal length of the eyepiece, fe = 2.5 cm Object distance for the objective lens, uo = −9.0 mm = −0.9 cm Least distance of distant vision, d = 25 cm Image distance for the eyepiece, ve = −d = −25 cm Object distance for the eyepiece =
Using the lens formula, we can obtain the value of as: 
We can also obtain the value of the image distance for the objective lens
using the lens formula.
The distance between the objective lens and the eyepiece 
The magnifying power of the microscope is calculated as:
Hence, the magnifying power of the microscope is 88.
Question 13. A small telescope has an objective lens of focal length 144 cm and an eyepiece of focal length 6.0 cm. What is the magnifying power of the telescope? What is the separation between the objective and the eyepiece?
Solution : Focal length of the objective lens, fo = 144 cm Focal length of the eyepiece, fe = 6.0 cm The magnifying power of the telescope is given as:
The separation between the objective lens and the eyepiece is calculated as:
Hence, the magnifying power of the telescope is 24 and the separation between the objective lens and the eyepiece is 150 cm.
Question 14. (a) A giant refracting telescope at an observatory has an objective lens of focal length 15 m. If an eyepiece of focal length 1.0 cm is used, what is the angular magnification of the telescope? (b) If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens? The diameter of the moon is 3.48 × 106 m, and the radius of lunar orbit is 3.8 × 108 m.
Solution : Focal length of the objective lens, fo = 15 m = 15 × 102 cm Focal length of the eyepiece, fe = 1.0 cm
(a) The angular magnification of a telescope is given as:
Hence, the angular magnification of the given refracting telescope is 1500. (b) Diameter of the moon, d = 3.48 × 106 m Radius of the lunar orbit, r0 = 3.8 × 108 m Let
be the diameter of the image of the moon formed by the objective lens. The angle subtended by the diameter of the moon is equal to the angle subtended by the image.
Hence, the diameter of the moon’s image formed by the objective lens is 13.74 cm
Question 15. Use the mirror equation to deduce that:
(a) an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
(b) a convex mirror always produces a virtual image independent of the location of the object.
(c) the virtual image produced by a convex mirror is always diminished in size and is located between the focus and the pole. (d) an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.
Solution : (a) For a concave mirror, the focal length (f) is negative. ∴f < 0 When the object is placed on the left side of the mirror, the object distance (u) is negative. ∴u < 0 For image distance v, we can write the lens formula as:
The object lies between f and 2f.
Using equation (1), we get:
Therefore, the image lies beyond 2f. (b) For a convex mirror, the focal length (f) is positive. ∴ f > 0 When the object is placed on the left side of the mirror, the object distance (u) is negative. ∴ u < 0 For image distance v, we have the mirror formula:
Thus, the image is formed on the back side of the mirror. Hence, a convex mirror always produces a virtual image, regardless of the object distance. (c) For a convex mirror, the focal length (f) is positive. ∴f > 0 When the object is placed on the left side of the mirror, the object distance (u) is negative, ∴u < 0 For image distance v, we have the mirror formula:
Hence, the image formed is diminished and is located between the focus (f) and the pole. (d) For a concave mirror, the focal length (f) is negative. ∴f < 0 When the object is placed on the left side of the mirror, the object distance (u) is negative. ∴u < 0 It is placed between the focus (f) and the pole.
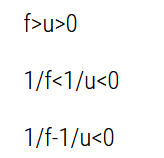
For image distance v, we have the mirror formula:
The image is formed on the right side of the mirror. Hence, it is a virtual image. For u < 0 and v > 0, we can write:
Magnification, m 
> 1 Hence, the formed image is enlarged.
Question 16. A small pin fixed on a table top is viewed from above from a distance of 50 cm. By what distance would the pin appear to be raised if it is viewed from the same point through a 15 cm thick glass slab held parallel to the table? Refractive index of glass = 1.5. Does the answer depend on the location of the slab? Solution : Actual depth of the pin, d = 15 cm Apparent dept of the pin =
Refractive index of glass, 
Ratio of actual depth to the apparent depth is equal to the refractive index of glass, i.e.
The distance at which the pin appears to be raised
For a small angle of incidence, this distance does not depend upon the location of the slab. Question 17. (a) Figure 9.28 shows a cross-section of a ‘light pipe’ made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44.
Solution : (a) Refractive index of the glass fibre,
Refractive index of the outer covering of the pipe, 
= 1.44 Angle of incidence = i Angle of refraction = r Angle of incidence at the interface = i’ The refractive index (μ) of the inner core − outer core interface is given as:
For the critical angle, total internal reflection (TIR) takes place only when 
Maximum angle of reflection, 
Let, 
be the maximum angle of incidence. The refractive index at the air − glass interface, 
We have the relation for the maximum angles of incidence and reflection as:
Thus, all the rays incident at angles lying in the range 0 < i < 60° will suffer total internal reflection. (b) If the outer covering of the pipe is not present, then: Refractive index of the outer pipe,
For the angle of incidence i = 90°, we can write Snell’s law at the air − pipe interface as:
. Question 18. The image of a small electric bulb fixed on the wall of a room is to be obtained on the opposite wall 3 m away by means of a large convex lens. What is the maximum possible focal length of the lens required for the purpose?
Solution : Distance between the object and the image, d = 3 m Maximum focal length of the convex lens =
For real images, the maximum focal length is given as:
Hence, for the required purpose, the maximum possible focal length of the convex lens is 0.75 m.
Question 19. A screen is placed 90 cm from an object. The image of the object on the screen is formed by a convex lens at two different locations separated by 20 cm. Determine the focal length of the lens.
Solution : Distance between the image (screen) and the object, D = 90 cm Distance between two locations of the convex lens, d = 20 cm Focal length of the lens = f Focal length is related to d and D as:
Therefore, the focal length of the convex lens is 21.39 cm.
Question 20.
(a) Determine the ‘effective focal length’ of the combination of the two lenses in Exercise 9.10, if they are placed 8.0 cm apart with their principal axes coincident. Does the answer depend on which side of the combination a beam of parallel light is incident? Is the notion of effective focal length of this system useful at all?
(b) An object 1.5 cm in size is placed on the side of the convex lens in the arrangement (a) above. The distance between the object and the convex lens is 40 cm. Determine the magnification produced by the two-lens system, and the size of the image.
Solution : Focal length of the convex lens, f1 = 30 cm Focal length of the concave lens, f2 = −20 cm Distance between the two lenses, d = 8.0 cm (a) When the parallel beam of light is incident on the convex lens first: According to the lens formula, we have:
Where,
= Object distance = ∞ v1 = Image distance 
The image will act as a virtual object for the concave lens. Applying lens formula to the concave lens, we have:
Where, 
= Object distance = (30 − d) = 30 − 8 = 22 cm 
= Image distance
The parallel incident beam appears to diverge from a point that is
from the centre of the combination of the two lenses.
(ii) When the parallel beam of light is incident, from the left, on the concave lens first: According to the lens formula, we have:
Where, = Object distance = −∞ = Image distance 
The image will act as a real object for the convex lens. Applying lens formula to the convex lens, we have:
Where, = Object distance = −(20 + d) = −(20 + 8) = −28 cm = Image distance 
Hence, the parallel incident beam appear to diverge from a point that is (420 − 4) 416 cm from the left of the centre of the combination of the two lenses. The answer does depend on the side of the combination at which the parallel beam of light is incident. The notion of effective focal length does not seem to be useful for this combination.
(b) Height of the image, h1 = 1.5 cm Object distance from the side of the convex lens,
According to the lens formula:
Where, 
= Image distance 
Magnification, 
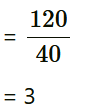
Hence, the magnification due to the convex lens is 3. The image formed by the convex lens acts as an object for the concave lens.
According to the lens formula:
Where, = Object distance = +(120 − 8) = 112 cm. = Image distance 
Magnification, 
Hence, the magnification due to the concave lens is
. The magnification produced by the combination of the two lenses is calculated as:
The magnification of the combination is given as:
Where, h1 = Object size = 1.5 cm h2 = Size of the image
Hence, the height of the image is 0.98 cm.
Question 21. At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is 1.524.
Solution : The incident, refracted, and emergent rays associated with a glass prism ABC are shown in the given figure.
Angle of prism, ∠A = 60° Refractive index of the prism, µ = 1.524
= Incident angle 
= Refracted angle 
= Angle of incidence at the face AC e = Emergent angle = 90° According to Snell’s law, for face AC, we can have: 
It is clear from the figure that angle
According to Snell’s law, we have the relation:
Hence, the angle of incidence is 29.75°. Question 22. A card sheet divided into squares each of size 1 mm2 is being viewed at a distance of 9 cm through a magnifying glass (a converging lens of focal length 9 cm) held close to the eye. (a) What is the magnification produced by the lens? How much is the area of each square in the virtual image? (b) What is the angular magnification (magnifying power) of the lens? (c) Is the magnification in (a) equal to the magnifying power in (b)? Explain.
Solution : Note : Here we took focal Length as 10 cm because if we take it as 9 cm then image distance will be zero ,which does not make any sense. (a) Area of each square, A = 1 mm2 Object distance, u = −9 cm Focal length of a converging lens, f = 9 cm For image distance v, the lens formula can be written as:
Magnification, 
∴Area of each square in the virtual image = (10)2A = 102 × 1 = 100 mm2 = 1 cm2 (b) Magnifying power of the lens
(c) The magnification in (a) is not the same as the magnifying power in (b). The magnification magnitude is
and the magnifying power is 
. The two quantities will be equal when the image is formed at the near point (25 cm). Question 23. (a) At what distance should the lens be held from the figure in Exercise 9.29 in order to view the squares distinctly with the maximum possible magnifying power?
(b) What is the magnification in this case?
(c) Is the magnification equal to the magnifying power in this case? Explain.
Solution : (a) The maximum possible magnification is obtained when the image is formed at the near point (d = 25 cm). Image distance, v = −d = −25 cm Focal length, f = 10 cm Object distance = u According to the lens formula, we have:
Hence, to view the squares distinctly, the lens should be kept 7.14 cm away from them. (b) Magnification =
(c) Magnifying power = 
Since the image is formed at the near point (25 cm), the magnifying power is equal to the magnitude of magnification. Question 24. What should be the distance between the object in Exercise 9.23 and the magnifying glass if the virtual image of each square in the figure is to have an area of 6.25 mm2
. Would you be able to see the squares distinctly with your eyes very close to the magnifier?
Solution : Area of the virtual image of each square, A = 6.25 mm2 Area of each square, A0 = 1 mm2 Hence, the linear magnification of the object can be calculated as:
Focal length of the magnifying glass, f = 10 cm According to the lens formula, we have the relation:
The virtual image is formed at a distance of 15 cm, which is less than the near point (i.e., 25 cm) of a normal eye. Hence, it cannot be seen by the eyes distinctly.
Question 25. Answer the following questions:
(a) The angle subtended at the eye by an object is equal to the angle subtended at the eye by the virtual image produced by a magnifying glass. In what sense then does a magnifying glass provide angular magnification?
(b) In viewing through a magnifying glass, one usually positions one’s eyes very close to the lens. Does angular magnification change if the eye is moved back?
(c) Magnifying power of a simple microscope is inversely proportional to the focal length of the lens. What then stops us from using a convex lens of smaller and smaller focal length and achieving greater and greater magnifying power?
(d) Why must both the objective and the eyepiece of a compound microscope have short focal lengths?
(e) When viewing through a compound microscope, our eyes should be positioned not on the eyepiece but a short distance away from it for best viewing. Why? How much should be that short distance between the eye and eyepiece?
Solution : (a)Though the image size is bigger than the object, the angular size of the image is equal to the angular size of the object. A magnifying glass helps one see the objects placed closer than the least distance of distinct vision (i.e., 25 cm). A closer object causes a larger angular size. A magnifying glass provides angular magnification. Without magnification, the object cannot be placed closer to the eye. With magnification, the object can be placed much closer to the eye.
(b) Yes, the angular magnification changes. When the distance between the eye and a magnifying glass is increased, the angular magnification decreases a little. This is because the angle subtended at the eye is slightly less than the angle subtended at the lens. Image distance does not have any effect on angular magnification.
(c) The focal length of a convex lens cannot be decreased by a greater amount. This is because making lenses having very small focal lengths is not easy. Spherical and chromatic aberrations are produced by a convex lens having a very small focal length.
(d) The angular magnification produced by the eyepiece of a compound microscope is
Where, fe = Focal length of the eyepiece It can be inferred that if fe is small, then angular magnification of the eyepiece will be large. The angular magnification of the objective lens of a compound microscope is given as
Where, 
= Object distance for the objective lens 
= Focal length of the objective The magnification is large when > . In the case of a microscope, the object is kept close to the objective lens. Hence, the object distance is very little. Since is small, will be even smaller. Therefore, 
and are both small in the given condition. (e)When we place our eyes too close to the eyepiece of a compound microscope, we are unable to collect much refracted light. As a result, the field of view decreases substantially. Hence, the clarity of the image gets blurred. The best position of the eye for viewing through a compound microscope is at the eye-ring attached to the eyepiece. The precise location of the eye depends on the separation between the objective lens and the eyepiece.
Question 26. An angular magnification (magnifying power) of 30X is desired using an objective of focal length 1.25 cm and an eyepiece of focal length 5 cm. How will you set up the compound microscope?
Solution : Focal length of the objective lens,
= 1.25 cm Focal length of the eyepiece, fe = 5 cm Least distance of distinct vision, d = 25 cm Angular magnification of the compound microscope = 30X Total magnifying power of the compound microscope, m = 30 The angular magnification of the eyepiece is given by the relation:
The angular magnification of the objective lens (mo) is related to me as:
= m 
Applying the lens formula for the objective lens:
The object should be placed 1.5 cm away from the objective lens to obtain the desired magnification. Applying the lens formula for the eyepiece:
Where, 
= Image distance for the eyepiece = −d = −25 cm 
= Object distance for the eyepiece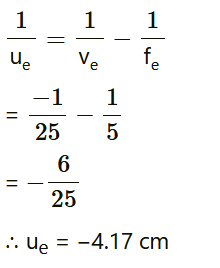 
Separation between the objective lens and the eyepiece 
Therefore, the separation between the objective lens and the eyepiece should be 11.67 cm.
Question 27. A small telescope has an objective lens of focal length 140 cm and an eyepiece of focal length 5.0 cm. What is the magnifying power of the telescope for viewing distant objects when (a) the telescope is in normal adjustment (i.e., when the final image is at infinity)? (b) the final image is formed at the least distance of distinct vision (25 cm)? Solution : Focal length of the objective lens,
= 140 cm Focal length of the eyepiece, fe = 5 cm Least distance of distinct vision, d = 25 cm (a) When the telescope is in normal adjustment, its magnifying power is given as: 
(b) When the final image is formed at d,the magnifying power of the telescope is given as:
Question 28. (a) For the telescope described in Exercise 9.34 (a), what is the separation between the objective lens and the eyepiece?
(b) If this telescope is used to view a 100 m tall tower 3 km away, what is the height of the image of the tower formed by the objective lens?
(c) What is the height of the final image of the tower if it is formed at 25 cm?
Solution : Focal length of the objective lens, fo = 140 cm Focal length of the eyepiece, fe = 5 cm (a) In normal adjustment, the separation between the objective lens and the eyepiece
(b) Height of the tower, h1 = 100 m Distance of the tower (object) from the telescope, u = 3 km = 3000 m The angle subtended by the tower at the telescope is given as:
The angle subtended by the image produced by the objective lens is given as:
Where, h2 = Height of the image of the tower formed by the objective lens
Therefore, the objective lens forms a 4.7 cm tall image of the tower. (c) Image is formed at a distance, d = 25 cm The magnification of the eyepiece is given by the relation:
Height of the final image 
Hence, the height of the final image of the tower is 28.2 cm.Question 29. A Cassegrain telescope uses two mirrors as shown in Fig. 9.33. Such a telescope is built with the mirrors 20 mm apart. If the radius of curvature of the large mirror is 220 mm and the small mirror is 140 mm, where will the final image of an object at infinity be?
Solution : The following figure shows a Cassegrain telescope consisting of a concave mirror and a convex mirror.
Distance between the objective mirror and the secondary mirror, d = 20 mm Radius of curvature of the objective mirror, R1 = 220 mm Hence, focal length of the objective mirror,
Radius of curvature of the secondary mirror, R1 = 140 mm Hence, focal length of the secondary mirror,
The image of an object placed at infinity, formed by the objective mirror, will act as a virtual object for the secondary mirror. Hence, the virtual object distance for the secondary mirror,
Applying the mirror formula for the secondary mirror, we can calculate image distance (v)as:
Hence, the final image will be formed 315 mm away from the secondary mirror. Question 30. Light incident normally on a plane mirror attached to a galvanometer coil retraces backwards as shown in Fig. 9.36. A current in the coil produces a deflection of 3.5° of the mirror. What is the displacement of the reflected spot of light on a screen placed 1.5 m away?
Solution : Angle of deflection, θ = 3.5° Distance of the screen from the mirror, D = 1.5 m The reflected rays get deflected by an amount twice the angle of deflection i.e., 2θ= 7.0° The displacement (d) of the reflected spot of light on the screen is given as:
Hence, the displacement of the reflected spot of light is 18.4 cm.
Ray Optics Class 12 Important Concepts Explained
Along with the Exercise-Wise NCERT Solutions for Chapter 9, students should also learn about these important concepts included in the chapter:
What is Reflection of Light?
Reflection of light deals with the bouncing back of light rays from reflecting surfaces such as plane and spherical mirrors. Image formation is explained using ray diagrams and mirror formulae.
What is Refraction of Light?
Refraction is the bending of light when it passes from one medium to another due to a change in its speed. Laws of refraction and refractive index play a key role in solving numerical problems.
What is the use of Optical Instruments?
Optical instruments such as microscopes and telescopes use lenses and mirrors to produce magnified images. Their working is explained using ray diagrams and magnification formulae.
NCERT Solutions For Class 12 Physics Chapter 9 FAQs
What is covered in Class 12 Physics Chapter 9 Ray Optics and Optical Instruments?
This chapter covers reflection and refraction of light, image formation by mirrors and lenses, and the working of optical instruments such as microscopes and telescopes.
Are NCERT Solutions enough for Ray Optics Class 12 board exams?
Yes, NCERT Solutions are sufficient for board exams as most questions are directly based on NCERT theory, formulas, and numerical problems from this chapter.
Why is Ray Optics important in Class 12 Physics?
Ray Optics is important because it forms the foundation of geometrical optics and has high weightage in board exams, especially numerical and diagram-based questions.
How are magnification and focal length related in lenses?
Magnification produced by a lens is directly related to the focal length. For convex lenses, the magnification is positive, and for concave lenses, it is negative.
What are the uses of optical instruments like microscopes and telescopes?
Microscopes are used for magnifying small objects, allowing detailed examination. Telescopes are designed to observe distant objects, like stars and planets, providing magnified and clear views.
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2026 Physicswallah Limited All rights reserved.