
The acceleration of an object's center of mass , a fundamental concept in physics, is determined by the net external force applied to it, as described by Newton's second law This law applies to both translational and rotational motion. Internal forces within the object do not affect the center of mass acceleration due to Newton's third law. This concept plays a pivotal role in understanding how objects respond to external influences and is crucial in classical mechanics.
Definition of Center of Mass
For a system of \(n\) particles with masses m 1 , m 2 , ..., m n and positions (x 1 , y 1 , z 1 ), (x 2 , y 2 , z 2 ), ...,(x n , y n , z n ), the center of mass is defined as:
In 1D (along the x-axis):
![]()
In 2D (along the x and y axes):
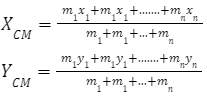
In 3D (along the x, y, and z axes):
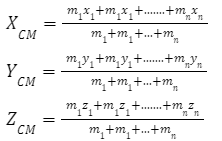
Also Check - Velocity Time Graph Formula
Velocity of Center of Mass
The velocity of the center of mass (CoM) is a fundamental concept in physics that plays a crucial role in understanding the motion of objects and systems. The center of mass is a theoretical point within an object or a system that behaves as if all the mass were concentrated at that single point. The velocity of the center of mass describes the motion of this point, which simplifies the analysis of complex motions and interactions.
Definition and Calculation:
The velocity of the center of mass V is the rate of change of the center of mass's position with respect to time. Mathematically, it can be expressed as:
V CM = Δ r cm/Δ t
Where:
- V is the velocity of the center of mass.
- r is the change in position vector of the center of mass.
- t is the change in time.
For an extended object with a continuous distribution of mass, the velocity of the center of mass can also be expressed as an integral:
V CM = 1/ M∫ vdm
Where:
- v is the velocity vector of the center of mass.
- M is the total mass of the object.
- dm is the velocity vector of an infinitesimal mass element \( dm \) within the object.
Significance:
Understanding the velocity of the center of mass is essential for several reasons:
- Simplification of Motion Analysis: By focusing on the motion of the center of mass, the analysis of the motion of an object or system can be simplified, especially when dealing with complex shapes and external forces.
- Predicting Trajectories: In situations where objects are subject to external forces like gravity or friction, understanding the center of mass's velocity helps predict their trajectories and overall motion.
- Collisions and Impulse: The center of mass plays a key role in collision physics and the concept of impulse. In many collision scenarios, only the center of mass motion needs to be considered.
- Stability and Equilibrium: The stability of objects is often determined by the relative positions of their center of mass and the point of support. Systems tend to be most stable when the center of mass is positioned low.
Also Check - Centre of Mass for n particle System Formula
Acceleration Of Center Of Mass
Center of Mass (COM): The center of mass of an object is the point at which its entire mass can be considered to be concentrated, as if all the mass were concentrated at that point. In simpler terms, it's the average position of the mass distribution within the object.
Newton's Second Law of Motion: This law states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. Mathematically, it's represented as:
F = m • a
Where:
- F is the net external force acting on the object.
- m is the total mass of the object.
- a is the acceleration of the center of mass.
Deriving the Equation for Center of Mass Acceleration:
The acceleration of the center of mass can be derived by considering the relationship between the net external force and the motion of the object. When external forces act on an object, the object accelerates as a whole. These external forces might include things like gravitational forces, applied forces, friction, etc.
When you sum up all the forces acting on an object and equate them to the mass of the object times its acceleration, you get:
∑F = m • a
This equation holds true for each component of the forces in different directions.
Internal Forces: One crucial aspect to note is that the internal forces between particles within the object don't directly affect the acceleration of the center of mass. This is due to Newton's third law of motion, which states that for every action, there is an equal and opposite reaction. Internal forces within an object will create pairs of forces that cancel each other out when considering the motion of the entire object. Therefore, they do not contribute to the acceleration of the center of mass.
Conservation of Momentum: The acceleration of the center of mass is also linked to the concept of momentum. The rate of change of the total momentum of an object is equal to the net external force applied to it. Mathematically, this is represented as:
F = d/ dt ( m • V com )
Where:
- V com is the velocity of the center of mass.
By rearranging this equation and considering the fact that acceleration is the derivative of velocity with respect to time, you can arrive at the equation F = m • a .
In summary, the acceleration of the center of mass of an object is determined by the net external force acting on the object. Internal forces do not affect the acceleration of the center of mass due to Newton's third law. This concept is fundamental in understanding the motion of objects and is a cornerstone of classical mechanics.
Also Check - Velocity Of Centre Of Mass Formula
Examples For Better Understanding
- High Jump Technique:
Imagine a high jumper going over the bar. As the jumper bends their body to clear the bar, their limbs extend outward. Despite the limbs' varying speeds, the center of mass velocity remains constant. This showcases how the center of mass motion simplifies complex body movements.
- Diver's Perfect Entry:
When a diver performs a perfect entry into the water, their body remains streamlined. The center of mass follows a smooth trajectory, minimizing resistance and achieving a graceful entry. This demonstrates how manipulating the center of mass velocity affects motion quality.
- Spacecraft Gravity Assist:
Spacecraft often use the gravitational pull of planets for speed boosts. The center of mass velocity guides these maneuvers. For instance, the Voyager spacecraft used Jupiter's gravity to increase its velocity, enabling it to explore the outer solar system more efficiently.
- Tightrope Walking:
Tightrope walkers maintain a slow and controlled center of mass velocity, enhancing stability. Their arms may move for balance, but their main body's motion is deliberately managed to prevent falling.
- Figure Skating Spins:
In figure skating, during spins, the skater pulls their arms closer to their body. This decreases the moment of inertia and increases the center of mass velocity, causing the skater to spin faster due to the conservation of angular momentum.
- Earth's Moon:
The Moon's center of mass velocity allows it to stay in orbit around the Earth. Despite the Moon's complex motions, its center of mass follows a predictable path, allowing astronomers to accurately predict lunar behavior.
- Acrobatic Stunts:
In circus performances, acrobats fly through the air, performing flips and twists. The center of mass velocity guides their overall motion, enabling them to complete complex aerial maneuvers.
- Balance in Martial Arts:
Martial artists use their center of mass velocity to maintain balance while executing powerful strikes or kicks. They adjust their body movements to control their center of mass and remain stable.
- Golf Swing Analysis:
In golf, the player's swing involves precise control of the center of mass velocity. Properly timed motions maximize club head speed while ensuring balance and accuracy.
- Artificial Satellites:
The center of mass velocity is crucial for placing satellites in precise orbits. Engineers must calculate and control the center of mass velocity to achieve desired trajectories and functionalities.
These extraordinary examples highlight how the concept of center of mass velocity governs the behavior of objects and systems across diverse scenarios, from sports and art to space exploration and engineering.
Applications Of Velocity Of Center Of Mass
The concept of the velocity of the center of mass has a wide range of applications across various fields of science, engineering, and everyday life. Here are some notable applications:
- Mechanics and Dynamics:
- Projectile Motion: Understanding the center of mass velocity is crucial for predicting the trajectory of projectiles like rockets, bullets, and sports balls.
- Collision Analysis: In collisions between objects, the behavior of the center of mass velocity provides insights into the outcome of the collision and the conservation of momentum.
- Astronomy and Space Exploration:
- Orbital Mechanics: The center of mass velocity is used to calculate the orbital trajectories of planets, satellites, and spacecraft in space.
- Interplanetary Missions: Spacecraft trajectories, such as slingshot maneuvers using a planet's gravity, rely on precise calculations of center of mass velocity.
- Engineering:
- Vehicle Dynamics: In automotive engineering, understanding the center of mass velocity is crucial for designing vehicles with optimal handling, stability, and safety.
- Aircraft Control: The center of mass velocity is essential in designing aircraft for stability and maneuverability.
- Structural Engineering: For buildings and structures, knowledge of center of mass velocity helps in assessing stability and potential vibrations.
- Biomechanics and Sports:
- Sports Performance: Understanding the center of mass velocity is essential for optimizing movements in sports like gymnastics, diving, figure skating, and others.
- Biomechanical Analysis: In biomechanics research, center of mass velocity is used to study human gait, posture, and balance.
- Robotics and Control Systems:
- Robotic Motion: Designing and programming robots to move efficiently and stably relies on controlling the center of mass velocity.
- Balancing Robots: Center of mass velocity calculations are used in developing self-balancing robots and vehicles.
- Astronomy and Cosmology:
- Galactic Motion: The concept of center of mass velocity helps astronomers understand the motion of galaxies in the universe and their interactions.
- Stellar Orbits: Center of mass velocity is used to study the orbits of binary star systems.
- Earth Sciences:
- Plate Tectonics: Center of mass velocity calculations are used to study the movement of tectonic plates and predict earthquake and volcanic activities.
- Ocean Currents: In oceanography, center of mass velocity is considered when studying ocean currents and their impact on climate.
- Architecture and Design:
- Structural Stability: Architects and engineers consider center of mass velocity when designing buildings to ensure stability against forces like wind and earthquakes.
- Film and Animation:
- Animation Realism: Animators use the principles of center of mass velocity to create realistic and physically accurate movements in animated characters and objects.
These applications highlight the pervasive role that the concept of center of mass velocity plays in understanding, predicting, and designing various physical phenomena and systems in our world, from the macroscopic scale of celestial bodies to the intricate details of human movements and technology.
Acceleration Of Centre Of Mass FAQs
What is center of mass acceleration?
How is it affected by internal forces?
Can it change in complex scenarios?
What's the link to momentum conservation?
Why is it important?










