The
center of mass
(COM) is a fundamental concept in physics that describes the average position of the mass of an object or a system of objects. It simplifies the study of the motion and dynamics of complex systems by treating them as a single point particle located at the center of mass. This concept is applicable in various fields of physics, including mechanics, astronomy, and engineering.
Definition of Center of Mass
For a system of \(n\) particles with masses m
1
, m
2
, ..., m
n
and positions (x
1
, y
1
, z
1
), (x
2
, y
2
, z
2
), ...,(x
n
, y
n
, z
n
), the center of mass is defined as:
In 1D (along the x-axis):
In 2D (along the x and y axes):
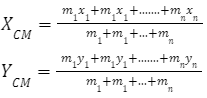
In 3D (along the x, y, and z axes):
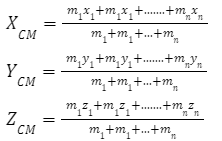
Also Check -
Equation of Motion in One Dimension Formula
Properties and Significance
-
Equivalent Particle :
The center of mass behaves as if all the mass of the system were concentrated at that point. When external forces act on a system, the system's motion can often be described as the motion of its center of mass under the influence of these forces.
-
Conservation of Linear Momentum
: In an isolated system (no external forces), the total linear momentum of the system remains constant unless acted upon by external forces. The motion of the center of mass reflects this conservation.
-
Balancing :
The concept of center of mass helps understand the stability and balance of objects. An object is stable when its center of mass is over its base of support.
-
Projectile Motion
: In projectile motion, the motion of an object can be divided into the motion of the center of mass and the motion around it (rotation).
-
Collision Physics :
When objects collide, the conservation of linear momentum and kinetic energy can be analyzed more conveniently by considering the center of mass frame of reference.
-
Orbital Motion :
The concept is crucial in astronomy for understanding the motion of planets, satellites, and celestial bodies around a common center of mass.
Merits of Center of Mass
The concept of the center of mass (COM) offers several advantages and benefits across various fields of science, engineering, and everyday life. Here are some of the key advantages of using the center of mass:
-
Simplification of Analysis:
The center of mass allows complex systems to be treated as a single point particle with concentrated mass. This simplifies the analysis of motion, dynamics, and interactions of objects or systems, reducing complex problems to simpler ones.
-
Conservation Laws:
In systems where external forces are negligible, the center of mass remains in uniform motion (Newton's first law). Also, the conservation of linear momentum and kinetic energy can be easily understood and applied using the concept of center of mass.
-
Efficient Problem Solving:
The center of mass enables efficient problem-solving in various scenarios such as collisions, projectile motion, and rotational dynamics. It reduces the complexity of calculations and provides a straightforward approach.
-
Stability and Balance:
The concept is essential for understanding the stability and balance of objects. Engineers and designers use the center of mass to ensure that structures, vehicles, and machines are stable and safe to use.
-
Design and Optimization:
Engineers and architects use the center of mass to design objects and structures for optimal performance. This applies to everything from vehicles and aircraft to sculptures and buildings.
-
Predicting Motion:
The center of mass provides insights into the motion of complex systems. For instance, in sports like gymnastics or diving, understanding the motion of the center of mass helps athletes perform complex maneuvers.
-
Real-World Applications:
The concept has practical applications in fields like aerospace engineering, automotive design, sports training, and art, contributing to the efficiency, safety, and aesthetics of various products and processes.
-
Educational Tool:
The center of mass is often used as an educational tool to introduce and teach concepts of physics. It provides a tangible way to illustrate theoretical principles.
-
Rigorous Analysis:
In advanced physics and engineering, the center of mass helps analyze the behavior of objects under various forces and interactions, enabling the prediction of complex behaviors.
-
Frame of Reference:
The center of mass serves as a convenient frame of reference for analyzing the motion of a system as a whole, separating it from motion related to rotation or internal motion.
-
Consistency in Modeling:
In simulations and modeling, using the center of mass helps maintain consistency and accuracy when predicting the behavior of objects and systems.
-
Safety and Efficiency in Operations:
Industries involving transportation, manufacturing, and construction use the center of mass to ensure safety and efficiency in operations that involve lifting, moving, and balancing heavy objects.
Also Check -
Displacement Time Graph Formula
Center of Mass for Continuous Distributions
For a continuous distribution of mass, the center of mass can be found using integration. In one dimension, the formula becomes:
X
CM
=∫
xdm/∫
dm
Similar formulas can be derived for two and three dimensions.
The center of mass is a powerful concept that simplifies the analysis of complex systems by reducing them to a single point. It's used across various physics disciplines and provides insights into the motion, stability, and interactions of objects and systems.
The center of mass of various shapes can be calculated using integration and geometry. Here, I'll provide you with the formulas for finding the center of mass for some common shapes.
-
Uniform Rod:
A uniform rod with length \(L\) and mass \(M\) has its center of mass at its midpoint:
X=L/2
-
Uniform Plate:
A uniform plate or sheet with mass \(M\) and area \(A\) has its center of mass at the intersection of its diagonals:
For 2D center of mass:
-
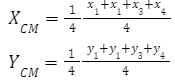
Triangle:
For a triangle with base \(b\) and height \(h\), the center of mass is located along the median lines, one-third of the way from the base to the tip along the height:
-
Rectangle:
For a rectangle with sides \(a\) and \(b\), the center of mass is at the intersection of its diagonals:
X=a/2
Y=b/2
-
Circle:
For a circular disk with radius \(r\), the center of mass is at the center of the circle:
X=0
Y=0
-
Semi-Circle
:
For a semi-circle with radius \(r\), the center of mass is along the diameter line at a distance of
4r
3
from the curved side.
-
Cylinder:
For a solid cylinder with radius \(r\) and height \(h\), the center of mass is at the center of the cylinder:
X=0
Y=0
Z=h/2
-
Sphere:
For a solid sphere with radius \(r\), the center of mass is at the center of the sphere:
X=0
Y=0
Z=0
These formulas provide the coordinates of the center of mass for various simple shapes. For more complex shapes, the center of mass can be calculated using integration techniques. Remember that the center of mass depends on the distribution of mass within the object, so uniformity assumptions are often made for simpler calculations.
Also Check -
Velocity Time Graph Formula
Applications of Center of Mass
The concept of the center of mass (COM) has numerous applications across various fields of physics, engineering, and everyday life. Here are some important applications of the center of mass:
-
Mechanics and Dynamics:
- Projectile Motion:
The center of mass simplifies the analysis of projectile motion by allowing us to treat the entire motion as a parabolic trajectory of the center of mass.
- Collisions:
When objects collide, the conservation of momentum and kinetic energy can be analyzed more easily using the concept of center of mass.
- Rotational Motion:
In rigid body dynamics, the motion of an object can be divided into the translational motion of the center of mass and the rotational motion about the center of mass.
- Stability and Equilibrium:
The center of mass helps determine the stability of objects. An object is stable when its center of mass is above its base of support.
-
Astronomy:
- Celestial Bodies:
The concept of center of mass is crucial in understanding the motion of planets, moons, satellites, and other celestial bodies in the universe.
-
Engineering:
- Design and Balance:
Engineers use the concept of center of mass to design stable structures, vehicles, and machines. It's important for ensuring proper balance and functionality.
- Structural Analysis:
In structural engineering, the distribution of mass and moments about the center of mass helps analyze the behavior of structures under various loads.
-
Statics:
- Statics Problems:
Solving statics problems involving distributed loads, beams, and structures is made easier by considering the equilibrium of forces and moments at the center of mass.
-
Art and Design:
- Sculpture and Art:
Artists and sculptors use the concept of center of mass to create balanced and aesthetically pleasing sculptures and artworks.
-
Sports and Athletics:
- High Jump and Pole Vault:
Athletes use the concept of center of mass to optimize their techniques in events like high jump and pole vault to clear the bar.
-
Aviation and Aerospace:
- Aircraft Design:
Engineers design aircraft with consideration for the center of mass to ensure stability and proper control during flight.
-
Vehicle Dynamics:
- Vehicle Handling:
In automotive engineering, understanding the center of mass helps design vehicles that handle well and have good stability during acceleration, braking, and turning.
-
Balancing Everyday Objects:
- Balancing Act:
When you balance a pencil on your finger, you're essentially finding the point where its center of mass lies to keep it upright.
-
Industrial Processes:
- Manufacturing:
In manufacturing, understanding the center of mass of objects is important for handling and transportation processes.
-
Architecture:
- Building Stability:
Architects and engineers consider the center of mass of buildings to ensure structural stability, especially in tall structures.
These are just a few examples of how the concept of center of mass plays a pivotal role in understanding and solving problems in various fields. It simplifies complex systems, helps in making accurate predictions, and aids in designing functional and balanced structures and systems.
