Buoyancy Formula - Definition, Limitations and Considerations
The buoyancy formula builds upon Archimedes' principle and relates the buoyant force to the properties of the object and the fluid it is immersed in. The concept of buoyancy can be mathematically described using Archimedes' principle and the buoyancy formula
Murtaza Mushtaq26 Sept, 2023
Share
Buoyancy is a fundamental principle in fluid mechanics that explains why objects float or sink when placed in a fluid medium, such as water or air. It plays a crucial role in various scientific and engineering applications, from designing ships and submarines to understanding the behavior of hot air balloons and underwater vehicles. The concept of buoyancy can be mathematically described using Archimedes' principle and the buoyancy formula, which relates the buoyant force acting on an object to the density of the fluid it is immersed in, the volume of the object submerged, and the acceleration due to gravity.
In this comprehensive guide, we will delve into the details of the buoyancy formula, its derivation, and its applications in different fields.
1. Archimedes' Principle
Archimedes' principle is the foundational principle behind buoyancy. It states that when an object is immersed in a fluid (liquid or gas), it experiences an upward force equal to the weight of the fluid displaced by the object. This upward force is known as the buoyant force (F_b). The principle was discovered by the ancient Greek mathematician and scientist Archimedes and is expressed mathematically as: F_b = ρ * V_displaced * g Where: - F_b is the buoyant force (in newtons, N). - ρ (rho) is the density of the fluid (in kilograms per cubic meter, kg/m³). - V_displaced is the volume of fluid displaced by the object (in cubic meters, m³). - g is the acceleration due to gravity (approximately 9.81 m/s² on Earth).Also Check - Heat Gain Formula
2. Buoyancy Formula
The buoyancy formula builds upon Archimedes' principle and relates the buoyant force to the properties of the object and the fluid it is immersed in. The formula is as follows: F_b = ρ_fluid * V_submerged * g Where: - F_b is the buoyant force (in newtons, N). - ρ_fluid (rho_sub) is the density of the fluid (in kilograms per cubic meter, kg/m³). - V_submerged is the volume of the object that is submerged in the fluid (in cubic meters, m³). - g is the acceleration due to gravity (in meters per second squared, m/s²). The buoyant force (F_b) acts in the upward direction and opposes the gravitational force acting on the object, causing it to float or rise in the fluid if F_b exceeds the object's weight. Conversely, if the buoyant force is less than the object's weight, the object will sink.Also Check - Induced Voltage Formula
3. Derivation of the Buoyancy Formula
To derive the buoyancy formula, we can start with Archimedes' principle and make some simplifying assumptions. Let's go through the derivation step by step: Step 1: Consider an object of volume V submerged in a fluid with density ρ_fluid. The weight of the object is given by: W = m * g Where: - W is the weight of the object (in newtons, N). - m is the mass of the object (in kilograms, kg). - g is the acceleration due to gravity (in meters per second squared, m/s²). Step 2: The mass of the object can be expressed in terms of its density (ρ_object) and volume (V_submerged): m = ρ_object * V_submerged Where: - ρ_object (rho_obj) is the density of the object (in kilograms per cubic meter, kg/m³). - V_submerged is the volume of the object submerged in the fluid (in cubic meters, m³). Step 3: Substitute the expression for mass (m) from Step 2 into the weight formula: W = ρ_object * V_submerged * g Step 4: Now, we can use Archimedes' principle, which states that the buoyant force (F_b) is equal to the weight of the fluid displaced by the object. The volume of fluid displaced (V_displaced) is the same as the volume of the submerged portion of the object (V_submerged): V_displaced = V_submerged Step 5: Apply Archimedes' principle to find the buoyant force (F_b): F_b = ρ_fluid * V_displaced * g Since V_displaced = V_submerged, we can rewrite the equation as: F_b = ρ_fluid * V_submerged * g Step 6: Now, compare the expression for F_b from Step 5 with the expression for the weight of the object (W) from Step 3: F_b = W Step 7: Equate the expressions for F_b and W: ρ_fluid * V_submerged * g = ρ_object * V_submerged * g Step 8: Cancel out the common factor of "g" from both sides of the equation: ρ_fluid * V_submerged = ρ_object * V_submerged Step 9: Finally, divide both sides by V_submerged to obtain the buoyancy formula: F_b = ρ_fluid * V_submerged * g And there you have it, the buoyancy formula derived from Archimedes' principle.Also Check - Diffraction Grating Formula
4. Applications of the Buoyancy Formula
The buoyancy formula has a wide range of applications in science and engineering. Here are some notable examples: Ship Design: Ship designers use the buoyancy formula to ensure that a ship's hull displaces enough water to provide sufficient buoyant force to support the weight of the ship and its cargo. This principle is essential for designing ships that can float and carry heavy loads across water bodies. Submarines: Submarines are designed to control their buoyancy by adjusting the amount of water in ballast tanks. By manipulating the volume of water in these tanks, submarines can either become positively buoyant (rise to the surface) or negatively buoyant (sink to lower depths). Understanding buoyancy is crucial for submarine navigation. Hot Air Balloons: Hot air balloons rely on the difference in density between hot air and cooler air to generate buoyant force. As the air inside the balloon is heated, it becomes less dense than the surrounding air, causing the balloon to rise. The buoyancy formula helps in understanding and predicting the behavior of hot air balloons. Aircraft Design: Aircraft designers consider buoyancy principles when designing and engineering aircraft. While aircraft primarily rely on aerodynamic lift to stay aloft, an understanding of buoyancy is essential for the design of amphibious aircraft and seaplanes that need to take off and land on water. Scuba Diving: Scuba divers use the concept of buoyancy to control their depth underwater. By adjusting the amount of air in their buoyancy compensators, divers can achieve neutral buoyancy, allowing them to hover at a specific depth without sinking or rising. Underwater Vehicles: Buoyancy is crucial for the design and operation of underwater vehicles, such as remotely operated vehicles (ROVs) and autonomous underwater vehicles (AUVs). Engineers must carefully control buoyancy to ensure these vehicles can navigate at various depths.5. Factors Affecting Buoyancy
Several factors can influence the buoyant force experienced by an object submerged in a fluid. Understanding these factors is essential for predicting and controlling buoyancy: Density of the Fluid (ρ_fluid): The density of the fluid in which the object is submerged is a critical factor. Objects are more buoyant in denser fluids and less buoyant in less dense fluids. For example, objects float more easily in saltwater (higher density) than in freshwater (lower density). Volume of the Object Submerged (V_submerged): The volume of the object that is submerged in the fluid directly affects the buoyant force. A larger submerged volume results in a greater buoyant force, while a smaller submerged volume leads to less buoyancy.Also Check - Electricity Formula
6. Acceleration Due to Gravity (g)
The acceleration due to gravity varies with location. On Earth, it is approximately 9.81 m/s², but it can differ slightly at different altitudes and latitudes. In space or on celestial bodies like the Moon, the value of g is significantly lower, affecting buoyancy calculations in those environments.- Buoyancy and Density: To understand the relationship between buoyancy and density further, let's examine some scenarios:
- Object Less Dense Than the Fluid: When an object is less dense than the fluid it is immersed in, it will float. In this case, the buoyant force is greater than the weight of the object. A classic example is a wooden boat floating on water.
- Object Equal in Density to the Fluid: If the object's density is equal to the density of the fluid, it will neither sink nor float. It will remain suspended at a specific depth, a state known as neutral buoyancy. This concept is crucial in scuba diving, where divers aim to achieve neutral buoyancy to hover underwater.
- Object More Dense Than the Fluid: When an object is more dense than the fluid it is in, it will sink. The buoyant force is insufficient to counteract the weight of the object. An example is a stone sinking in water.
7. Buoyancy and Archimedes' Principle:
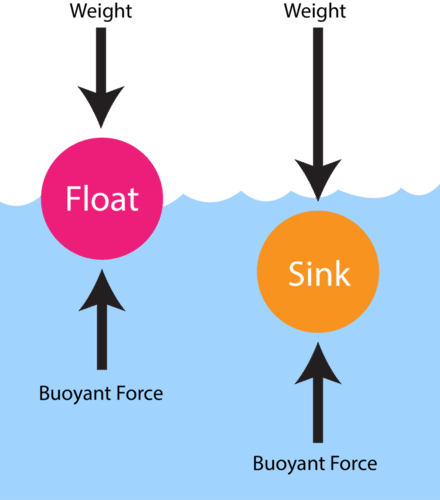
Archimedes' principle, which underlies the buoyancy formula, provides valuable insights into how objects interact with fluids. It states that the buoyant force is equal to the weight of the fluid displaced by the object. Here's a closer look at Archimedes' principle in action:- Buoyant Force Exceeds Weight: When the buoyant force (F_b) is greater than the weight of the object (W), the object experiences an upward force greater than its downward force due to gravity. This results in the object floating on the surface of the fluid or rising within it. The magnitude of the buoyant force determines how high the object will float.
- Buoyant Force Equals Weight: When the buoyant force equals the weight of the object, the object remains suspended in the fluid without sinking or rising. This condition is referred to as neutral buoyancy. It's commonly observed in scenarios where an object's density matches that of the surrounding fluid.
- Buoyant Force Is Less Than Weight: If the buoyant force is less than the weight of the object, the object will sink in the fluid. In this case, the object's weight overcomes the upward force exerted by the fluid, causing the object to descend.
8. Practical Buoyancy Calculations
To apply the buoyancy formula in real-world scenarios, you'll typically need to know the density of the fluid (ρ_fluid) and the volume of the object submerged (V_submerged). Here's a step-by-step guide to performing practical buoyancy calculations: Step 1: Determine the Density of the Fluid (ρ_fluid): Identify the fluid in which the object is immersed and find its density in kilograms per cubic meter (kg/m³). You may need to consult reference tables or measure it directly using appropriate equipment. Step 2: Determine the Volume of the Object Submerged (V_submerged): Measure or calculate the volume of the object that is submerged in the fluid. This may involve simple geometric calculations for regular shapes or more complex methods for irregular objects. Step 3: Calculate the Buoyant Force (F_b): Use the buoyancy formula to calculate the buoyant force acting on the object: F_b = ρ_fluid * V_submerged * g Step 4: Compare Buoyant Force and Weight: Compare the calculated buoyant force (F_b) to the weight of the object (W). If F_b is greater than W, the object will float or rise; if F_b equals W, the object will remain suspended at a specific depth (neutral buoyancy); if F_b is less than W, the object will sink.9. Limitations and Considerations
While the buoyancy formula is a powerful tool for understanding the behavior of objects in fluids, it has some limitations and considerations:- Simplified Assumptions: The formula assumes that the fluid and the object are incompressible and that there are no other forces or effects at play. In reality, fluids can be compressible, and additional factors like turbulence and surface tension can affect buoyancy.
- Temperature Variations: The density of a fluid can vary with temperature. In situations where temperature changes significantly, the buoyant force may change accordingly.
- Salinity and Composition: The composition and salinity of a fluid can also impact its density. For example, seawater has a higher density than freshwater due to its salt content. Buoyancy calculations should consider these variations.
- Pressure Effects: In deep-sea environments, the pressure can significantly affect the density of the fluid. Engineers and scientists working in these conditions must account for pressure effects when calculating buoyancy.
- Irregularly Shaped Objects: Calculating the submerged volume (V_submerged) can be challenging for irregularly shaped objects. Advanced techniques, such as numerical methods or computer simulations, may be necessary in such cases.
Buoyancy Formula FAQs
What is the significance of neutral buoyancy, and how is it achieved?
Neutral buoyancy is a state in which an object neither sinks nor rises when submerged in a fluid. It is crucial for various applications, such as scuba diving and underwater robotics. To achieve neutral buoyancy, the object's density must match the density of the surrounding fluid. This can be accomplished by adjusting the object's weight, volume, or both.
How does buoyancy work in space, where there is no gravity?
In space, there is no gravitational acceleration, so objects don't experience weight in the traditional sense. However, the concept of buoyancy still applies when objects are submerged in fluids within spacecraft. In microgravity environments, buoyancy helps determine how fluids behave and how equipment like water tanks and life support systems operate.
Can the buoyancy formula be used for gases like helium in airships?
Yes, the buoyancy formula can be applied to gases as well. When dealing with lighter-than-air gases like helium or hydrogen inside an airship, you can calculate buoyancy by considering the density of the gas compared to the surrounding air. The principles are the same, but you'll use the density of the gas instead of the fluid.
How does temperature affect buoyancy?
Temperature can influence buoyancy by changing the density of a fluid. As a fluid's temperature increases, its density generally decreases, making it less buoyant. Conversely, a decrease in temperature increases fluid density, leading to greater buoyancy. Understanding these temperature effects is crucial in applications like weather forecasting and oceanography.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.