Introduction

Certain Forms of the Equations of circles

(a) Centre (h, k) and radius r

The equation is (x – h) ² + (y - k) ² = r ₂ (1)

(b) General form of the equation of a circle is

x ² + y ² + 2gx + 2fy + c = 0 (2)

If we compare equation (1) and (2) we get the centre of (2) as (-g, -f) and radius =

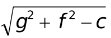
(c) Equation of a circle on the segment joining (x ₁ , y ₁ ) and (x ₂ , y ₂ ) as the ends of a diameter is given by (x – x ₁ )(x – x ₂ ) + (y – y ₁ )(y – y ₂ ) = 0 (3)

(d) General equation of a circle which passes through A(x ₁ , y1) and B(x ₂ , y ₂ ) may be written as

(x – x ₁ )(x – x ₂ ) + (y – y ₁ )( y – y2) + λ 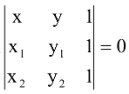(4)

(e) The equation of the circle through 3 non-collinear points A(x1, y1), B(x2, y2) and C(x3, y3) is

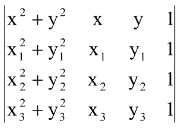= 0

Position of a Point

The point P(x ₁ , y ₁ ) lies outside or inside the circle

S = x ² + y ² + 2gx + 2fy + c = 0 according as

S ₁ = 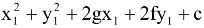> or < 0