Charles Law Formula: Definition, Equation, Derivation and Examples

Charles Law Formula: Charles Law, also known as the law of volumes, asserts that the volume of an ideal gas is directly tied to its absolute temperature under constant pressure conditions. This law, attributed to the French physicist Jacques Charles in 1780, remains valid when the pressure exerted on a sample of dry gas remains consistent.

Charles's Law provides insight into how gases behave when subjected to temperature changes. Essentially, as temperature rises, gas volume expands, and conversely, as temperature falls, gas volume contracts. This relationship can be expressed mathematically as:

V2/V1 = T2/T1

Alternatively, V1 * T2 = V2 * T1

This equation demonstrates that as the absolute temperature increases, the gas volume also increases proportionally. Charles's Law is a particular case of the ideal gas law and is applicable to ideal gasses held at a constant pressure while their temperature and volume change.

Also Check – Gibbs Free Energy Formula

Charles Law in Everyday Life

During winter, as temperatures drop, a basketball left outside on the ground shrinks. This underscores the importance of checking tire pressure when driving in cold weather. On a hot day, if you overfill a tube placed in a pool, it can expand and potentially burst due to increased temperature. This principle also applies to pop-up turkey thermometers, which work based on Charles's Law. In car engines, Charles's Law plays a role in understanding the behavior of gases as they heat up or cool down.

Also Check – Percent by Weight Formula

Charles Law Formula

The formula for Charles's Law is expressed as follows:

VI / TI = VF / TF

Where:

VI represents the initial volume.

VF represents the final volume.

TI represents the initial absolute temperature (measured in Kelvin).

TF represents the final absolute temperature (measured in Kelvin).

It's crucial to use absolute temperatures in Kelvin, rather than Celsius or Fahrenheit, when applying this formula.

Also Check – Electronegativity Formula

Derivation of Charles Law

As we are well aware, under constant pressure conditions, the volume of a fixed quantity of dry gas exhibits a direct relationship with absolute temperature, as elucidated by Charle’s law. This relationship is mathematically expressed as:

V ∝ T

Given this direct proportionality between V and T, we can establish an equivalence by introducing a constant, denoted as 'k':

V/T = constant = k

The value of 'k' is contingent upon factors such as the gas's pressure, the quantity of gas present, and the unit of volume utilized.

This relationship can also be expressed as:

V * T = k ——(1)

Let us designate V1 and T1 as the initial volume and temperature, respectively, of an ideal gas. Accordingly, equation (1) can be rewritten as:

V1/T1 = k ——(2)

Now, suppose we alter the gas's temperature to T2 or its volume to V2. We can formulate the following equation:

V2/T2 = k ——(3)

Equating equations 2 and 3, we derive:

V1/T1 = V2/T2

OR

V1T2 = V2T1

It is worth noting that when a fixed amount of gas is heated, increasing the temperature leads to an expansion in its volume. Conversely, reducing the temperature results in a contraction of the gas's volume. Notably, at 0 degrees Celsius, the gas's volume increases by 1/273 of its original volume for each one-degree increment in temperature.

Furthermore, it is crucial to emphasize that when applying Charle’s law, temperature must be measured in Kelvin, not Celsius or Fahrenheit. Kelvin temperature is synonymous with the absolute temperature scale. To convert temperatures from Celsius to Kelvin, you simply add 273 to the Celsius temperature.

In line with Charles’ law, which postulates that a gas's volume (V) is directly proportional to its temperature (T), it is imperative to use the Kelvin scale for temperature measurements.

Each unit increment on the Kelvin scale corresponds to a one-degree change in Celsius. Always bear in mind that the Kelvin scale's absolute zero point, denoted as 0 K, is equivalent to -273 degrees Celsius.

Moreover, when the mass and pressure of a gas remain constant, its density exhibits an inverse proportionality to temperature measured in Kelvin.

Also Check – Sodium Hydroxide Formula

Graphical Representation of Charles Law

The graphical representation of Charles's Law at constant pressure is known as an isobar or isopleth. This graph yields a straight line, and at -273.15 degrees Celsius, it reaches its lowest possible temperature.

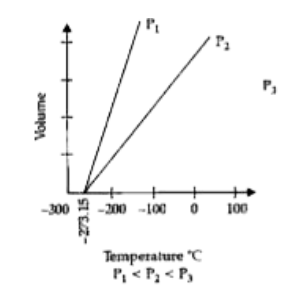
Charles's Law Formula Solved Example

Example 1: A gas occupies a volume of 2.5 L at a temperature of 27°C. What will be the volume of the gas at 127°C, assuming constant pressure?

Given:

V1 = 2.5 L

T1 = 27°C = 27 + 273 = 300 K

T2 = 127°C = 127 + 273 = 400 K

We want to find V2.

Using Charles's Law:

V1/T1 = V2/T2

Plugging in the values:

2.5/300 = V2/400

Solving for V2:

V2 = (2.5 * 400) / 300

V2 = 3.33 L

So, the volume of the gas at 127°C will be 3.33 liters.

Example 2: A gas occupies a volume of 100 mL at -10°C. What will be its volume at 50°C, assuming constant pressure?

Given:

V1 = 100 mL

T1 = -10°C = -10 + 273 = 263 K

T2 = 50°C = 50 + 273 = 323 K

We need to find V2.

Using Charles's Law:

V1/T1 = V2/T2

Plugging in the values:

100/263 = V2/323

Solving for V2:

V2 = (100 * 323) / 263

V2 = 122.21 mL

So, the volume of the gas at 50°C will be 122.21 mL.

Example 3: A gas occupies a volume of 4.0 L at 25°C. If the temperature is changed to 75°C, what will be the new volume of the gas, assuming constant pressure?

Given:

V1 = 4.0 L

T1 = 25°C = 25 + 273 = 298 K

T2 = 75°C = 75 + 273 = 348 K

We want to find V2.

Using Charles's Law:

V1/T1 = V2/T2

Put in the values:

4.0/298 = V2/348

Solving for V2:

V2 = (4.0 * 348) / 298

V2 = 4.68 L

So, the new volume of the gas at 75°C will be 4.68 liters.