Cone Formula - Equation And Examples
Cone Formula: The cone formula is used to calculate the volume and surface area of a cone, which has practical applications in various fields.
Murtaza Mushtaq31 Oct, 2023
Share
Cone Formula
Cone Formula : Cone is a fundamental geometric shape that finds applications in various fields, from mathematics to engineering and even in everyday objects. In this article, we'll delve into the cone formula, exploring its geometry and practical applications. Whether you're a student, a content writer, or simply someone curious about cones, this comprehensive guide will provide you with a solid understanding of this intriguing geometric figure. The Geometry of a Cone Cone Formula A cone is a three-dimensional geometric figure characterized by a circular base and a pointed apex. The essential geometric elements of a cone include:- Base Radius (r): This is the distance from the center of the base to any point on the circular edge. It plays a crucial role in determining the cone's properties.
- Slant Height (l): The slant height is the straight-line distance from the apex to any point on the edge of the base. It defines the cone's overall height and slant angle.
- Height (h): The height of a cone is the vertical distance from the apex to the center of the base. It's a fundamental parameter in cone calculations.
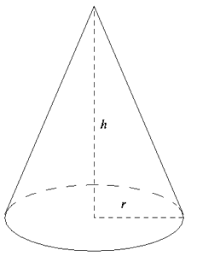
The Cone Formula
Slant Height
The Cone Formula for calculating the slant height of a cone is given by the Pythagorean Theorem, which relates the radius (r), the height (h), and the slant height (l) of the cone. Here's the formula:l = √(r² + h²)
In this formula: - "l" represents the slant height of the cone. - "r" is the radius of the base of the cone. - "h" is the height of the cone.Volume Of Cone
The Cone Formula for calculating the volume of a cone is:V = (1/3)πr²h
In this formula: - "V" represents the volume of the cone. - "π" is the mathematical constant Pi, approximately equal to 3.14159. - "r" is the radius of the base of the cone. - "h" is the height of the cone.Surface Area of Cone
The Cone Formula for calculating the surface area of a cone depends on the type of cone. For a right circular cone (the most common type), the surface area is given by:A = πr² + πr√(r² + h²)
In this formula: - "A" represents the surface area of the cone. - "π" is the mathematical constant Pi, approximately equal to 3.14159. - "r" is the radius of the base of the cone. - "h" is the height of the cone. The surface area of a right circular cone consists of two parts: the area of the base (πr²) and the lateral surface area (πr√(r² + h²)).Types of Cone
A cone is a fundamental three-dimensional geometric shape that has a circular base and tapers to a single point known as the apex. It's a shape we encounter in various aspects of our lives, from ice cream cones to traffic cones. In this article, we will delve into the different types of cones, their properties, and their applications.1. The Right Circular Cone
A right circular cone is perhaps the most common type of cone. It has a circular base and the apex lies directly above the center of the base. The axis, which is the line connecting the apex and the center of the base, is perpendicular to the base. This type of cone is encountered in everyday objects like traffic cones and party hats.Formula : The formula to calculate the volume of a right circular cone is V = (1/3)πr²h, where r is the radius of the base, and h is the height.
Also Check – Horsepower Formula
2. Oblique Cone
An oblique cone is any cone that is not a right circular cone. In this type, the apex may not be directly above the center of the base, and the axis is not perpendicular to the base. Oblique cones are less common but appear in various engineering and design applications.Formula : The volume of an oblique cone can still be calculated using the same formula V = (1/3)πr²h.
3. Perpendicular Cone
A perpendicular cone is a variation where the apex is above the center of the base, but the axis is not perpendicular to the base. It's a unique form that can be encountered in architectural designs and sculptures.Also Check – Shear Modulus Formula
Formula : The formula for calculating the volume of a perpendicular cone is the same as that of the right circular cone: V = (1/3)πr²h.
4. Truncated Cone
A truncated cone is formed when a smaller cone is removed from the top of a larger cone. It results in a shape resembling a frustum, and it's frequently used in engineering for structures like silos and hoppers.Formula : The volume of a truncated cone can be calculated using the formula for the volume of a frustum: V = (1/3)πh(R² + r² + (R * r)), where R is the radius of the larger base, r is the radius of the smaller base, and h is the height.
Also Check – Tangential Velocity Formula
5. Elliptical Cone
An elliptical cone is a variation where the base is not a perfect circle but an ellipse. This shape is encountered in some architectural designs and artistic sculptures.Formula : The formula for calculating the volume of an elliptical cone is V = (1/3)πabh, where 'a' and 'b' are the semi-major and semi-minor axes of the ellipse, and 'h' is the height.
Solved Examples Of Cone Formula
Problem: Find the volume of a cone with a base radius of 4 units and a height of 6 units. Step 1: Identify the Given Values In this problem, we have the following values: - Base Radius (r) = 4 units - Height (h) = 6 units Step 2: Apply the Volume Formula The volume of a cone is given by the formula: V = (1/3) * π * r^2 * h. Step 3: Substitute the Given Values V = (1/3) * π * (4^2) * 6 Step 4: Perform the Calculations V = (1/3) * π * 16 * 6 Now, calculate the value of 16 * 6. V = (1/3) * π * 96 Step 5: Calculate the Final Volume V = (96/3) * π V = 32π cubic units Step 6: Express the Result The volume of the cone is 32π cubic units. Problem 1: Find the surface area of a cone with a base radius of 5 units and a slant height of 8 units. Step 1: Given Values - Base Radius (r) = 5 units - Slant Height (l) = 8 units Step 2: Surface Area Formula The surface area of a cone is given by the formula: A = π * r * (r + l). Step 3: Substitute the Given Values A = π * 5 * (5 + 8) Step 4: Perform the Calculations A = π * 5 * 13 A = 65π square units Step 5: Express the Result The surface area of the cone is 65π square units. Problem 2: Find the volume of a cone with a base radius of 3.5 units and a height of 10 units. Step 1: Given Values - Base Radius (r) = 3.5 units - Height (h) = 10 units Step 2: Volume Formula The volume of a cone is given by the formula: V = (1/3) * π * r^2 * h. Step 3: Substitute the Given Values V = (1/3) * π * (3.5^2) * 10 Step 4: Perform the Calculations V = (1/3) * π * 12.25 * 10 V = (1/3) * π * 122.5 V = 40.83π cubic units Step 5: Express the Result The volume of the cone is approximately 40.83π cubic units. Problem 3: Find the slant height of a cone with a base radius of 6 units and a height of 8 units. Step 1: Given Values - Base Radius (r) = 6 units - Height (h) = 8 units Step 2: Slant Height Formula The slant height (l) can be found using the Pythagorean Theorem: r^2 + h^2 = l^2. Step 3: Substitute the Given Values (6^2) + (8^2) = l^2 36 + 64 = l^2 100 = l^2 l = √100 l = 10 units Step 4: Express the Result The slant height of the cone is 10 units. Problem 4: Find the volume of a cone with a base radius of 7 units and a height of 12 units. Step 1: Given Values - Base Radius (r) = 7 units - Height (h) = 12 units Step 2: Volume Formula V = (1/3) * π * r^2 * h Step 3: Substitute the Given Values V = (1/3) * π * (7^2) * 12 Step 4: Perform the Calculations V = (1/3) * π * 49 * 12 V = (1/3) * π * 588 V = 196π cubic units Step 5: Express the Result The volume of the cone is 196π cubic units. Problem 5: Find the surface area of a cone with a base radius of 6.5 units and a slant height of 10 units. Step 1: Given Values - Base Radius (r) = 6.5 units - Slant Height (l) = 10 units Step 2: Surface Area Formula A = π * r * (r + l) Step 3: Substitute the Given Values A = π * 6.5 * (6.5 + 10) Step 4: Perform the Calculations A = π * 6.5 * 16.5 A = 107.25π square units Step 5: Express the Result The surface area of the cone is approximately 107.25π square units. Problem 6: Find the slant height of a cone with a base radius of 8 units and a height of 15 units. Step 1: Given Values - Base Radius (r) = 8 units - Height (h) = 15 units Step 2: Slant Height Formula Using the Pythagorean Theorem: r^2 + h^2 = l^2 Step 3: Substitute the Given Values (8^2) + (15^2) = l^2 64 + 225 = l^2 289 = l^2 l = √289 l = 17 units Step 4: Express the Result The slant height of the cone is 17 units. Let's continue with more problems: Problem 7: Find the volume of a cone with a base radius of 3 units and a height of 9 units. Step 1: Given Values - Base Radius (r) = 3 units - Height (h) = 9 units Step 2: Volume Formula V = (1/3) * π * r^2 * h Step 3: Substitute the Given Values V = (1/3) * π * (3^2) * 9 Step 4: Perform the Calculations V = (1/3) * π * 9 * 9 V = (1/3) * π * 81 V = 27π cubic units Step 5: Express the Result The volume of the cone is 27π cubic units. Problem 8: Find the surface area of a cone with a base radius of 5.5 units and a slant height of 7 units. Step 1: Given Values - Base Radius (r) = 5.5 units - Slant Height (l) = 7 units Step 2: Surface Area Formula A = π * r * (r + l) Step 3: Substitute the Given Values A = π * 5.5 * (5.5 + 7) Step 4: Perform the Calculations A = π * 5.5 * 12.5 A = 68.75π square units Step 5: Express the Result The surface area of the cone is approximately 68.75π square units. Problem 9: Find the slant height of a cone with a base radius of 6.2 units and a height of 8.6 units . Step 1: Given Values - Base Radius (r) = 6.2 units - Height (h) = 8.6 units Step 2: Slant Height Formula Using the Pythagorean Theorem: r^2 + h^2 = l^2 Step 3: Substitute the Given Values (6.2^2) + (8.6^2) = l^2 38.44 + 73.96 = l^2 112.4 = l^2 l = √112.4 l ≈ 10.61 units Step 4: Express the Result The slant height of the cone is approximately 10.61 units. Problem 10: Find the volume of a cone with a base radius of 4.5 units and a height of 7.2 units. Step 1: Given Values - Base Radius (r) = 4.5 units - Height (h) = 7.2 units Step 2: Volume Formula V = (1/3) * π * r^2 * h Step 3: Substitute the Given Values V = (1/3) * π * (4.5^2) * 7.2 Step 4: Perform the Calculations V = (1/3) * π * 20.25 * 7.2 V = (1/3) * π * 145.8 V ≈ 484.62π cubic units Step 5: Express the Result The volume of the cone is approximately 484.62π cubic units.Cone Formula FAQs
What is the cone formula used for?
The cone formula is used to calculate the volume and surface area of a cone, which has practical applications in various fields.
How do I find the volume of a cone?
To find the volume of a cone, use the formula V = (1/3) * π * r^2 * h.
What is the surface area of a cone formula?
The formula to find the surface area of a cone is A = π * r * (r + l).
Can you explain the relationship between the base radius and slant height of a cone?
The base radius (r) and slant height (l) are related through the Pythagorean Theorem: r^2 + h^2 = l^2.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.