
Equation of a Straight Line Formula: The equation of a straight line is a fundamental concept in geometry and algebra, providing a mathematical representation of a straight line's properties. This equation is versatile and can be expressed in various forms, such as point-slope form, slope-intercept form, intercept form, and standard form. In this article, we will delve into the equation of a straight line, explore its different forms, and work through examples to enhance your comprehension.
Defining the Equation of a Straight Line
The equation of a straight line is a linear equation in two variables, usually denoted as x and y. It describes the relationship between the coordinates of all points lying on that line. This equation reveals crucial information about the line, including its slope (m), x-intercept, and y-intercept. Additionally, it aids in identifying points that lie on the line. Commonly, the equation of a straight line is determined using various forms, such as point-slope form, slope-intercept form, two-point form, and standard form, among others.
Also Check - Polynomials Formula
Equation of a Straight Line Formulas
The formula for the equation of a straight line varies depending on the available information about the line, such as its slope, intercepts, or specific points. Here are several formulas for representing the equation of a straight line:
| Different Forms of Straight Lines | Equation of Straight Line |
| Two Point-Form Given two points (x1, y1) and (x2, y2) on the line: | y - y1 = (y2 - y1)/(x2 - x1) (x - x1) |
| Point-Slope Form Given slope (m) and a point (x1, y1): | y - y1 = m (x - x1) |
| Slope-Intercept Form Given slope (m) and y-intercept (0, c): | y = mx + c |
| Intercept Form Given the x-intercept (a) and y-intercept (0, b): | x/a + y/b = 1 |
| Normal Form Given the angle (θ) made by the normal with the positive direction of the x-axis and the distance of the line from the origin (p): | x cos θ + y sin θ = p |
| General/Standard Form | ax + by = c |
| Equation of a Vertical Line For a vertical line passing through a point (a, b): | x = a |
| Equation of a Horizontal Line For a horizontal line passing through a point (a, b): | y = b |
We will explore each of these forms in detail in the following sections.
Forms of the Equation of a Straight Line
The equation that defines a straight line typically hinges on the concept of slope. When we consider a line labeled as 'l' and observe it making an angle of θ with respect to the positive direction of the x-axis, we refer to θ as the inclination of the line. In mathematical terms, the tangent of θ, denoted as tan θ, represents the slope of the line. It's crucial to recognize that the x-axis itself possesses a slope of 0. In fact, this characteristic extends to all lines that are parallel to the x-axis, as they too possess a slope of 0. Conversely, the slope of any line parallel to the y-axis, including the y-axis itself, is undefined.
With this foundational understanding of slope, let's delve into the different forms used to express equations of straight lines.
Also Check - Factorization Formula
Point-Slope Form
To establish the equation of a straight line with a given slope 'm' and passing through a specific point (x1, y1), we employ the point-slope form. This form is expressed as:
y-y1 = m(x-x1)
where (x, y) denotes any arbitrary point situated on the line.
Let's explore the process of deriving this point-slope form by utilizing the equation for the slope of a line. Consider a line characterized by a slope 'm,' and assume that (x1, y1) is a known point located on this line. Now, let's designate (x, y) as any other random point on this line, with its coordinates remaining unspecified. We start with the formula for calculating the slope of a line:
Slope= (Difference in x−coordinates) / (Difference in y−coordinates)
This equation can be expressed as:
m= x−x1 / y−y1
By multiplying both sides of this equation by (x - x1), we obtain:
m(x−x1)=(y−y1).
This can be rearranged as:
(y−y1)=m(x−x1).
Consequently, we have successfully demonstrated the validity of the point-slope form for representing the equation of a straight line.
Also Check - Data Handling Formula
Two Point Form
Let's explore the "Two Point Form" for the equation of a line. Imagine a line that passes through two distinct points, namely (x1, y1) and (x2, y2). To determine its slope, we apply the following formula:
m= x2−x1 / y2−y1
When we incorporate this slope formula into the previously discussed point-slope form, we arrive at the "Two Point Form," which is expressed as:
y−y1= x2−x1 / y2−y1 (x−x1)
This form allows us to define a line based on the coordinates of two specific points it traverses.
Also Check - Statistics FormulaSlope-Intercept Form
Now, let's consider a scenario where you are provided with a line characterized by its slope 'm' and its y-intercept. Imagine that this line crosses the y-axis at the point (0, c). By applying the point-slope form, we can derive the slope-intercept form of this line, which is expressed as:
y−c=m(x−0)⇒y=mx+c,
where 'c' represents the y-intercept. This particular form is commonly referred to as the "slope-intercept form" of a line.
It's worth noting that if the line instead intersects the x-axis at a point denoted as (d, 0), then the slope-intercept form of its equation can be represented as:
y=m(x−d).
Also Check - Probability Formula
Intercept Form
Let's examine the scenario where a line has x and y-intercepts at points (a, 0) and (0, b), respectively. To determine its slope, we can use the formula:
m= (0−a) / (b−0) = − a/b
Utilizing this slope, we can express the equation of the line using the point-slope form as follows:
y−0 = − a/b(x−a).
By multiplying both sides by 'a', we obtain:
ay=−bx+ab.
bx+ay=ab.
Finally, by dividing both sides by 'ab', we can express the equation as:
a/x+ b/y =1
Standard Form
The standard form for representing a straight line's equation is expressed as
ax+by=c, where 'a,' 'b,' and 'c' are real numbers. It is a versatile form that can be derived from various other forms of line equations. Let's illustrate this transformation with an example where we convert the equation
y=2x−1 into standard form.
To achieve this, we'll begin by subtracting
2x from both sides of the equation:
y−2x=2x−1−2x.
Simplifying further:
y−2x=−1.
Now, by rearranging the terms:
2x−y=1.
As a result, we successfully arrive at the standard form of the line's equation, which is
2x−y=1
Equation of a Straight Line on a Graph
In graphical representations, linear equations in one variable (x) produce vertical lines parallel to the y-axis, while equations in one variable (y) yield horizontal lines parallel to the x-axis. For linear equations in two variables (x and y), the graph forms a straight line with a specific slope. A positive slope indicates an increasing line from left to right, while a negative slope signifies a decreasing line.
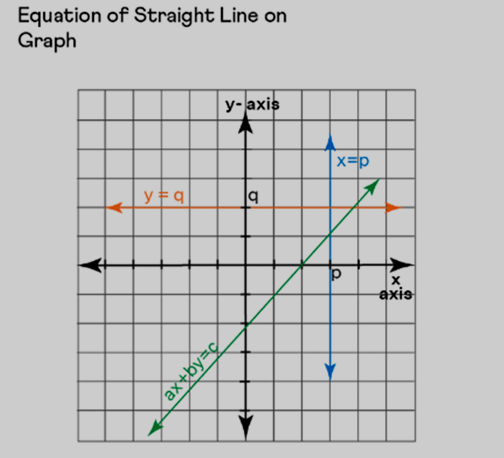
Important Notes on the Equation of a Straight Line
- The equation of a straight line is also referred to as a linear equation in two variables.
- When the product of slopes of two straight lines is -1, these lines are perpendicular to each other.
- Parallel lines share the same slope.
- Key equations include:
- Point Slope Form: (y - y1) = m (x - x1)
- Slope-Intercept Form: y = mx + c
- Standard Form: ax + by = c
Equation of a Straight Line Formula FAQs
What is the equation of a straight line?
What are the different forms of the equation of a straight line?
How do you find the equation of a line given two points?
What is the point-slope form of a line?
What does the slope of a line represent?










