Hypergeometric Distribution Formula, Definition and Examples
The hypergeometric distribution formula is particularly useful for scenarios where the outcomes are not independent, such as drawing items from a finite population without replacement,
Anchal Singh16 Oct, 2023
Share
The probability mass function (PMF) formula for the Hypergeometric Distribution Formula is as follows:
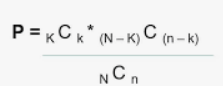P(X = k) = (Choose(K, k) * Choose(N - K, n - k)) / Choose(N, n)
Where:
P(X = k) is the probability of getting exactly k successes (items with a specific characteristic) in a sample of size n.
K is the total number of successes (items with the desired characteristic) in the population.
N is the total population size.
n is the sample size.
k is the desired number of successes in the sample.
Choose(n, k) represents combinations, often denoted as "n choose k."
This formula is used to calculate the probability of obtaining a specific number of successes in a finite population when drawing a sample without replacement.
What is the Hypergeometric Distribution?
The hypergeometric distribution formula is a probability distribution closely related to the binomial distribution. In fact, when your sample size is relatively small, say 5% or less of the population, the binomial distribution serves as a reliable approximation of the hypergeometric distribution. Therefore, a solid grasp of the binomial distribution and a reasonable level of comfort with the combinations formula are essential for a comprehensive understanding of the hypergeometric distribution formula.Hypergeometric Distribution Formula
The hypergeometric distribution formula is defined as where X is random variable is: Where:- K is the number of successes in the population
- k is the number of observed successes
- N is the population size
- n is the number of draws
Also Check – Logarithm Formula
Hypergeometric Distribution Example 1
To calculate the probability of drawing exactly 4 red cards from a deck containing 20 cards (6 red and 14 black) when drawing 5 cards randomly without replacement, you can express it as: P(4 red cards) = (Number of ways to select 4 red cards and 1 black card) / (Total number of possible 5-card samples) This formula helps you determine the probability of obtaining the desired outcome. Using the combination formula, the problem becomes: In shorthand, the above formula can be written as: (6C4*14C1)/20C5 where- 6C4 means that out of 6 possible red cards, we are choosing 4.
- 14C1 means that out of a possible 14 black cards, we’re choosing 1.
Also Check – Line and Angles Formula
Application of Hypergeometric Distribution Formula
The hypergeometric distribution formula finds applications in various real-life scenarios where you are dealing with non-replacement sampling, limited populations, and the calculation of probabilities. Here are a few examples of its applications:- Quality Control: In manufacturing and quality control processes, you might have a limited batch of items, and you want to calculate the probability of finding a certain number of defective items in a sample drawn without replacement. This is crucial for maintaining quality standards.
- Election Polling: When conducting political polls, you might want to predict the probability of a certain number of voters in a sample voting for a particular candidate. The hypergeometric distribution can be used to model this when you have a finite population of eligible voters.
- Sampling in Finite Populations : When conducting market research, you might have a limited database of potential customers. If you want to predict the probability of selecting a certain number of customers with specific characteristics in your sample, the hypergeometric distribution is useful.
- Game Shows: Game shows often involve selecting items without replacement. For instance, in a TV game show where contestants choose briefcases or boxes, the hypergeometric distribution can help calculate the likelihood of specific outcomes.
- Wildlife Conservation : Biologists studying animal populations in a specific area may use the hypergeometric distribution to estimate the probability of capturing a certain number of animals with specific traits or characteristics in a limited number of captures or observations.
- Forensic Analysis: In forensic science, when examining a finite set of characteristics in a population (e.g., DNA profiles, fingerprints, or other physical traits), the hypergeometric distribution can be used to calculate the probability of finding a specific set of characteristics in a random sample.
- Classroom Performance : If a teacher wants to assess the probability of randomly selecting a specific number of students with particular performance levels from a class, they can use the hypergeometric distribution.
- Inventory Management: In retail or manufacturing, when dealing with a limited supply of high-demand items or components, the hypergeometric distribution can help determine the likelihood of running out of a specific item or experiencing stockouts.
| Related Links | |
| Fibonacci Sequence Formula | Half Angle Formula |
| Exponential Formula | Geometric Series Formula |
H<span style=
What is the hypergeometric distribution?
The hypergeometric distribution is a probability distribution used to model situations where you draw items from a finite population without replacement. It calculates the probability of getting a specific number of successes (e.g., items with a certain characteristic) in the sample.
What are the key parameters of the hypergeometric distribution?
The key parameters are:
Population size (N): The total number of items in the population.
Number of successes in the population (K): The total number of items with the desired characteristic.
Sample size (n): The number of items drawn from the population without replacement.
Number of successes in the sample (k): The desired number of items with the characteristic in the sample.
When do you use the hypergeometric distribution?
The hypergeometric distribution is used when sampling without replacement from a finite population. Typical applications include quality control, election polling, market research, and situations where the trials are not independent.
How does the hypergeometric distribution differ from the binomial distribution?
The hypergeometric distribution is used when sampling without replacement, with the probability of success changing as items are drawn. The binomial distribution is used when sampling with replacement, and the trials are independent.
What happens when the sample size (n) approaches the population size (N)?
As n gets closer to N, the hypergeometric distribution approaches the binomial distribution because, with a large sample relative to the population, the impact of not replacing items becomes less significant.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.