
The Natural Log Formula Logarithms present an alternate representation of exponents, Comprehending logarithms isn't overly complex; it primarily involves recognizing that a logarithmic expression serves as an alternative to an exponential one. Let's articulate the natural log formula in terms of exponents: If e x =a, then log e a =x, and the converse holds true. Interpreting log e a =x can be verbalized as 'The logarithm of a with a base of e equals x.' Logarithms with the base e are termed natural logarithms.
What is the Natural Log Formula
Let's explore four natural log formulas that elucidate different properties of logarithms:
Product Rule: When dealing with the logarithm of a product of two numbers, it translates to the sum of the logarithms of the individual numbers.
log e (m⋅n)=log e (m)+log e (n)
Quotient Rule: The logarithm of a quotient of two numbers equates to the difference between the logarithms of the individual numbers.
log e ( n m )=log e (m)−log e (n)
Power Rule: The exponent of the argument within a logarithm can be moved in front of the logarithm.
log e (a m )=m⋅log e (a)
Change of Base Rule: This rule allows the alteration of the base of a logarithm using either of these expressions:
log e (a)= log c (e) log c (a)
or
log e (a)⋅log c (e)=log c (a)
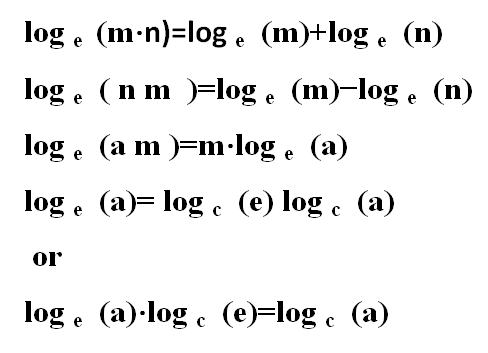
Natural Log Formula Solved Examples
Example 1: Determine the integer value of x using natural log formulas from the equation e 3x =9.
Solution: e 3x =9
ln(e 3x )=ln(9)
3x=ln(9)
x= ln(9) / 3
Example 2: Simplify the expression: 6ln e (y)+2ln e (4y)−ln e (8y 6 ) Solution:
6ln e (y)+2ln e (4y)−ln e (8y 6 )
=ln e (y 6 )+ln e ((4y) 2 )−ln e (8y 6 )
= ln e (y 6 )+ln e (16y 2 )−ln e (8y 6 )
= lne(y 6 ⋅16y 2 )−lne(8y 6 )
=lne(16y 8 )−lne(8y 6 )
=lne(16y 8 /8y 6 )
=lne(2y 2 )
Example 3: To solve for x in the equation e 2x =20
We start by taking the natural logarithm of both sides to isolate the variable x.
So, we apply the natural logarithm function (ln) to both sides of the equation: ln(e 2x )=ln(20)
The property of logarithms allows us to bring down the exponent as a multiplier: 2x⋅ln(e)=ln(20)
Since the natural logarithm of the base e is 1, we're left with:
2x=ln(20)
Finally, to solve for x, we divide both sides by 2:
x= ln(20) / 2
Example 4: In the expression 4lne(x)−lne(x 2 ), we want to simplify it by using the properties of logarithms.
We rewrite the expression using the properties of logarithms:
4lne(x)−lne(x 2 )
=lne(x 4 )−lne(x 2 )
=lne(x 4 /x 2 )
= lne(x 2 )
Example 5: Given the equations e x =7 and e 2x =49, we're tasked with finding the value of x.
From the first equation e x =7, we know that x=ln(7).
Using the second equation e 2x =49,
we substitute the value of x obtained earlier: e 2x =49
e 2ln(7) =49
(e ln(7) ) 2 =49
7 2 =49
This shows that the value of x is indeed ln(7), and by extension, the value of x is 2, since e 2x =49 holds true when x=2.
These step-by-step explanations illustrate how natural logarithm formulas are applied to solve equations and simplify expressions involving logarithmic functions.
| Related Links | |
| Foil Formula | Function Notation Formula |
| Hexagonal Pyramid Formula | Hypothesis Testing Formula |
Natural Log Formula FAQs
What is the natural log formula?
How do you solve equations using natural logarithms?
What are some essential properties of natural logarithms?
Why are natural logarithms significant in mathematics?










