NCERT Solutions for Class 12 Maths Chapter 11 Exercise 11.2

NCERT Solutions for Class 12 Maths Chapter 11 Exercise 11.2: Exercise 11.2 of NCERT Class 12 Maths Chapter 11, Three-Dimensional Geometry, focuses on the equation of a line in space using vector and Cartesian forms.

This chapter is an essential part of the CBSE Class 12 syllabus, covering key concepts like the direction cosines and ratios of a line, equations of a line in different forms, and the angle between two lines. According to the CBSE 12th exam pattern, questions from this chapter frequently appear in board exams, including derivations, conceptual questions, and numerical problems. Mastering these solutions helps students strengthen their understanding and perform well in both board exams and competitive exams like JEE and CUET.

NCERT Solutions for Class 12 Maths Chapter 11 Miscellaneous Exercise

NCERT Solutions for Class 12 Maths Chapter 11 Exercise 11.2 Overview

Chapter 11 of NCERT Class 12 Mathematics, Three-Dimensional Geometry, explores the representation of points, lines, and planes in three-dimensional space using both Cartesian and vector forms. It introduces concepts such as direction cosines, direction ratios, equations of lines and planes, and the relationships between them.

Students learn to calculate angles between lines and planes, determine distances between points and geometric entities, and find points of intersection. These concepts are crucial for spatial visualization and have practical applications in physics, engineering, navigation, and computer graphics. Mastering this chapter enhances problem-solving skills in higher mathematics and real-world scenarios.

Checkout Class 12th Books from PW Store

NCERT Solutions for Class 12 Maths Chapter 11 Exercise 11.2

Solve The Following Questions of NCERT Solutions for Class 12 Maths Chapter 11 Exercise 11.2

Question 1. Show that the three lines with direction cosines  are mutually perpendicular. 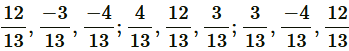Solution : Two lines with direction cosines, l ₁ , m ₁ , n ₁ and l ₂ , m ₂ , n ₂ , are perpendicular to each other, if l ₁ l ₂ + m ₁ m ₂ + n ₁ n ₂ = 0 Therefore, the lines are perpendicular. Thus, all the lines are mutually perpendicular.

NCERT Solutions for Class 12 Maths Chapter 11 Exercise 11.1

Buy Now CBSE Class 12 Sample Paper Books

Question 2. Show that the line through the points (1, −1, 2) (3, 4, −2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).

 Solution : Let AB be the line joining the points, (1, −1, 2) and (3, 4, − 2), and CD be the line joining the points, (0, 3, 2) and (3, 5, 6). The direction ratios, a ₁ , b ₁ , c ₁ , of AB are (3 − 1), (4 − (−1)), and (−2 − 2) i.e., 2, 5, and −4. The direction ratios, a ₂ , b ₂ , c ₂ , of CD are (3 − 0), (5 − 3), and (6 −2) i.e., 3, 2, and 4. AB and CD will be perpendicular to each other, if a ₁ a ₂ + b ₁ b ₂ + c ₁ c ₂ = 0 a ₁ a ₂ + b ₁ b ₂ + c ₁ c ₂ = 2 × 3 + 5 × 2 + (− 4) × 4 = 6 + 10 − 16 = 0 Therefore, AB and CD are perpendicular to each other.

NCERT Solutions for Class 12 Maths Chapter 11 Exercise 11.3

Question 3. Show that the line through points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (−1, −2, 1), (1, 2, 5).

 Solution : Let AB be the line through the points, (4, 7, 8) and (2, 3, 4), and CD be the line through the points, (−1, −2, 1) and (1, 2, 5). The directions ratios, a ₁ , b ₁ , c ₁ , of AB are (2 − 4), (3 − 7), and (4 − 8) i.e., −2, −4, and −4. The direction ratios, a ₂ , b ₂ , c ₂ , of CD are (1 − (−1)), (2 − (−2)), and (5 − 1) i.e., 2, 4, and 4. AB will be parallel to CD, if a1/a2 = b1/b2 = c1/c2 a1/a2 = -2/2 = -1 b1/b2 = -4/4 = -1 c1/c2 = -4/4 = -1 ∴a1/a2 = b1/b2 = c1/c2 Thus, AB is parallel to CD.

 Question 4. Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector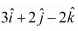

 Solution : It is given that the line passes through the point A (1, 2, 3). Therefore, the position vector through A is

It is known that the line which passes through point A and parallel to is given by λ is a constant.

This is the required equation of the line. 

Question 5. Find the equation of the line in vector and in Cartesian form that passes through the point with position vector  and is in the direction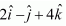

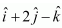
Solution : It is given that the line passes through the point with position vector

It is known that a line through a point with position vector and parallel to is given by the equation, This is the required equation of the line in vector form.

Eliminating λ, we obtain the Cartesian form equation as 

 Question 6. Find the Cartesian equation of the line which passes through the point (−2, 4, −5) and parallel to the line given by

 Solution : It is given that the line passes through the point (−2, 4, −5) and is parallel to

The direction ratios of the line, 

 ,

are 3, 5, and 6. The required line is parallel to 

Therefore, its direction ratios are 3 k , 5 k , and 6 k , where k ≠ 0 It is known that the equation of the line through the point ( x ₁ , y ₁ , z ₁ ) and with direction ratios, a , b , c , is given by Therefore the equation of the required line is

 Question 7. The Cartesian equation of a line is  Write its vector form.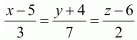

  Solution : The Cartesian equation of the line is ....(1)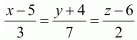

 The given line passes through the point (5, −4, 6). The position vector of this point is

Also, the direction ratios of the given line are 3, 7, and 2. This means that the line is in the direction of vector,  It is known that the line through position vector and in the direction of the vector is given by the equation,

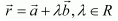
This is the required equation of the given line in vector form.

Question 8. Find the vector and Cartesian equations of the line that passes through the origin and (5, −2, 3). Solution :

The required line passes through the origin. Therefore, its position vector is given by, = 0           

     .....(1) The direction ratios of the line through origin and (5, −2, 3) are (5 − 0) = 5, (−2 − 0) = −2, (3 − 0) = 3

 The line is parallel to the vector given by the equation,

The equation of the line in vector form through a point with position vector and parallel to is,

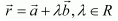
 The equation of the line through the point ( x ₁ , y ₁ , z ₁ ) and direction ratios a , b , c is given by,

Therefore, the equation of the required linein the Cartesian form is

  Question 9. Find vector and Cartesian equations of the line that passes through the points (3, −2, −5), (3, −2, 6).

 Solution : Let the line passing through the points, P (3, −2, −5) and Q (3, −2, 6), be PQ.

Since PQ passes through P (3, −2, −5), its position vector is given by, 

The direction ratios of PQ are given by, (3 − 3) = 0, (−2 + 2) = 0, (6 + 5) = 11

The equation of the vector in the direction of PQ is

 The equation of PQ in vector form is given by,

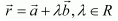
The equation of PQ in Cartesian form is i.e.,

 Question 10. Find the angle between the following pairs of lines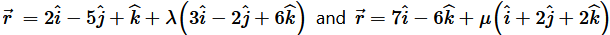: (i) (ii) 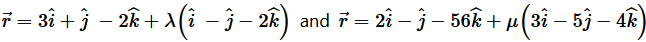Solution : (i) Let Q be the angle between the given lines. The angle

between the given pairs of lines is given by

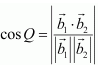
The given lines are parallel to the vectors,

 , respectively.

 (ii) The given lines are parallel to the vectors, respectively.

Question 11. Find the angle between the following pair of lines

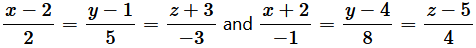(i) (ii) 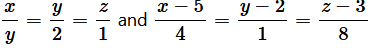Solution : Let ₁ and ₂ be the vectors parallel to the pair of lines, 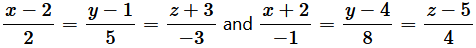, respectively. (ii) Let _{1 2} be the vectors parallel to the given pair of lines, 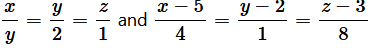, respectively. Question 12. Find the values of p so that the lines   are at right angles. Solution : The given equations can be written in the standard form as The direction ratios of the lines are respectively Two lines with direction ratios , a ₁ , b ₁ , c ₁ and a ₂ , b ₂ , c ₂ , are perpendicular to each other, if a ₁ a ₂ + b ₁ b ₂ + c ₁ c ₂ = 0

 Question 13. Show that the lines are perpendicular to each other.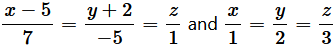

Solution : The equations of the given lines are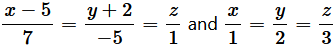

 The direction ratios of the given lines are 7, −5, 1 and 1, 2, 3 respectively.

Two lines with direction ratios,  a ₁ , b ₁ , c ₁ and a ₂ , b ₂ , c ₂ ,

are perpendicular to each other,

if  a ₁ a ₂ + b ₁ b ₂ + c ₁ c ₂ = 0 ∴ 7 × 1 + (−5) × 2 + 1 × 3 = 7 − 10 + 3 = 0

Therefore, the given lines are perpendicular to each other.  Question 14. Find the shortest distance between the lines Solution : The equations of the given lines are Since, the shortest distance between the two skew lines is given by Therefore, the shortest distance between the two lines is 3√2/2 units. Question 15. Find the shortest distance between the lines .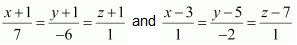

  Solution : The given lines are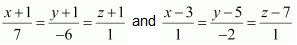

 It is known that the shortest distance between the two lines, ,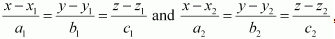

 is given by Comparing this equation we have Since distance is always non-negative, the distance between the given lines is 2√29 units.

 Question 16. Find the shortest distance between the lines whose vector equations are

 Solution : The given lines are It is known that the shortest distance between the lines,   is given by, .....

(1)

Comparing the given equations with , we obtain 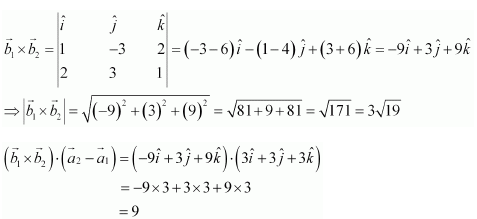Substituting all the values in equation

(1), we obtain 

Therefore, the shortest distance between the two given lines is 3/√19 units. 

Question 17. Find the shortest distance between the lines whose vector equations are

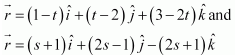
  Solution : The given lines are It is known that the shortest distance between the lines, is given by, For the given equations, Substituting all the values in equation (3), we obtain Therefore, the shortest distance between the lines is 8/√29 units.