
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.1 (Continuity and Differentiability)
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.1 Continuity and Differentiability is prepared by the academic team of Physics Wallah. We have prepared NCERT Solutions for all exercises of Chapter 5. Given below is step by step solutions of all questions given in NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.1 Continuity and Differentiability.NCERT Solutions for Class 12 Maths Chapter 5 Miscellaneous Exercise
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.1 Overview
NCERT Solutions for Class 12 Maths Chapter 5 contains all the important topics for the exams. Our experts created these questions for the students to ace the examination. This article contains all the important questions and their easy to understand answers for the better understanding. Students are advised to go through these questions to clarify their concepts better. These questions are created to help students in the better understanding of the NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.1.NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.1
Solve The Following Questions NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.1 Continuity and Differentiability:
Question 1. Prove that the function f(x) = 5x - 3 is continuous at x = 0, at x = - 3 and x = 5 Solution :
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.2
Question 2. Examine the continuity of the function f(x) = 2x 2 - 1 at x = 3 Solution : Thus, f is continuous at x = 3
Thus, f is continuous at x = 3
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.3
Question 3. Examine the following functions for continuity. (a)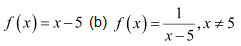 (c)
(c)
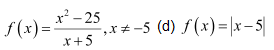 Solution :
Solution :


 Therefore, f is continuous at all real numbers greater than 5.
Hence, f is continuous at every real number and therefore, it is a continuous function.
Therefore, f is continuous at all real numbers greater than 5.
Hence, f is continuous at every real number and therefore, it is a continuous function.
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.4
Question 4. Prove that the function f(x) = x n is continuous at x = n, where n is a positive integer. Solution : The given function is f (x) = xn It is evident that f is defined at all positive integers, n, and its value at n is nn. Therefore, f is continuous at n, where n is a positive integer.
Therefore, f is continuous at n, where n is a positive integer.
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.5
Question 5. Is the function f defined by continuous at x = 0? At x = 1? At x = 2?
Solution :
The given function f is
continuous at x = 0? At x = 1? At x = 2?
Solution :
The given function f is
 At x = 0,
It is evident that f is defined at 0 and its value at 0 is 0.
At x = 0,
It is evident that f is defined at 0 and its value at 0 is 0.
 Therefore, f is continuous at x = 0
At x = 1,
f is defined at 1 and its value at 1 is 1.
The left hand limit of f at x = 1 is,
Therefore, f is continuous at x = 0
At x = 1,
f is defined at 1 and its value at 1 is 1.
The left hand limit of f at x = 1 is,
 The right hand limit of f at x = 1 is,
The right hand limit of f at x = 1 is,
 Therefore, f is not continuous at x = 1
At x = 2,
f is defined at 2 and its value at 2 is 5.
Therefore, f is not continuous at x = 1
At x = 2,
f is defined at 2 and its value at 2 is 5.
 Therefore, f is continuous at x = 2
Therefore, f is continuous at x = 2
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.6
Question 6. Find all points of discontinuity of f, where f is defined by Solution :
Solution :
 It is observed that the left and right hand limit of f at x = 2 do not coincide.
Therefore, f is not continuous at x = 2
Hence, x = 2 is the only point of discontinuity of f.
It is observed that the left and right hand limit of f at x = 2 do not coincide.
Therefore, f is not continuous at x = 2
Hence, x = 2 is the only point of discontinuity of f.
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.7
Question 7. Find all points of discontinuity of f, where f is defined by Solution :
The given function f is
Solution :
The given function f is
 The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
 Therefore, f is continuous at all points x, such that x < −3
Case II:
Therefore, f is continuous at all points x, such that x < −3
Case II:
 Therefore, f is continuous at x = −3
Case III:
Therefore, f is continuous at x = −3
Case III:
 Therefore, f is continuous in (−3, 3).
Case IV:
If c = 3, then the left hand limit of f at x = 3 is,
Therefore, f is continuous in (−3, 3).
Case IV:
If c = 3, then the left hand limit of f at x = 3 is,
 The right hand limit of f at x = 3 is,
The right hand limit of f at x = 3 is,
 It is observed that the left and right hand limit of f at x = 3 do not coincide.
Therefore, f is not continuous at x = 3
Case V:
It is observed that the left and right hand limit of f at x = 3 do not coincide.
Therefore, f is not continuous at x = 3
Case V:
 Therefore, f is continuous at all points x, such that x > 3
Hence, x = 3 is the only point of discontinuity of f.
Therefore, f is continuous at all points x, such that x > 3
Hence, x = 3 is the only point of discontinuity of f.
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.8
Question 8. Find all points of discontinuity of f, where f is defined by Solution :
Solution :


NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.3
Question 9. Find all points of discontinuity of f, where f is defined by Solution :
Solution :

NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.4
Question 10. Find all points of discontinuity of f, where f is defined by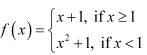 Solution :
Solution :
 Therefore,
f
is continuous at all points
x
, such that
x
> 1
Hence, the given function
f
has no point of discontinuity.
Therefore,
f
is continuous at all points
x
, such that
x
> 1
Hence, the given function
f
has no point of discontinuity.
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.5
Question 11. Find all points of discontinuity of f, where f is defined by Solution :
Solution :
 Therefore, f is continuous at all points x, such that x > 2
Thus, the given function f is continuous at every point on the real line.
Hence, f has no point of discontinuity.
Therefore, f is continuous at all points x, such that x > 2
Thus, the given function f is continuous at every point on the real line.
Hence, f has no point of discontinuity.
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.6
Question 12. Find all points of discontinuity of f, where f is defined by Solution :
The given function f is
Solution :
The given function f is
 The given function f is defined at all the points of the real line.
Let c be a point on the real line.
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
 Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observation, it can be concluded that x = 1 is the only point of discontinuity of f.
Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observation, it can be concluded that x = 1 is the only point of discontinuity of f.
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.7
Question 13. Is the function defined by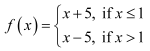 a continuous function?
Solution :
The given function is
a continuous function?
Solution :
The given function is
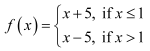 The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
 Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observation, it can be concluded that x = 1 is the only point of discontinuity of f.
Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observation, it can be concluded that x = 1 is the only point of discontinuity of f.
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.8
Question 14. Discuss the continuity of the function f, where f is defined by f = Solution :
The given function is f =
Solution :
The given function is f =
 The given function is defined at all points of the interval [0, 10].
Let c be a point in the interval [0, 10].
Case I:
The given function is defined at all points of the interval [0, 10].
Let c be a point in the interval [0, 10].
Case I:

 Therefore, f is continuous at all points of the interval (3, 10].
Hence, f is not continuous at x = 1 and x = 3
Question
15. Discuss the continuity of the function f, where f is defined by
Therefore, f is continuous at all points of the interval (3, 10].
Hence, f is not continuous at x = 1 and x = 3
Question
15. Discuss the continuity of the function f, where f is defined by
 Solution :
The given function is
Solution :
The given function is
 The given function is defined at all points of the real line.
Let c be a point on the real line.
Case I:
The given function is defined at all points of the real line.
Let c be a point on the real line.
Case I:

 Question
16. Discuss the continuity of the function f, where f is defined by
Question
16. Discuss the continuity of the function f, where f is defined by
 Solution :
The given function f is
Solution :
The given function f is
 The given function is defined at all points of the real line.
Let c be a point on the real line.
Case I:
The given function is defined at all points of the real line.
Let c be a point on the real line.
Case I:

 Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observations, it can be concluded that f is continuous at all points of the real line.
Question
17. Find the relationship between a and b so that the function f defined by
Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observations, it can be concluded that f is continuous at all points of the real line.
Question
17. Find the relationship between a and b so that the function f defined by
 is continuous at x = 3.
Solution :
The given function f is
is continuous at x = 3.
Solution :
The given function f is
 If f is continuous at x = 3, then
If f is continuous at x = 3, then
 Question 18. For what value of λ is the function defined by
Question 18. For what value of λ is the function defined by
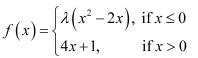 continuous at x = 0?
What about continuity at x = 1?
Solution :
The given function f is
continuous at x = 0?
What about continuity at x = 1?
Solution :
The given function f is
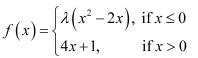 If f is continuous at x = 0, then
If f is continuous at x = 0, then
 Therefore, for any values of λ, f is continuous at x = 1
Question
19. Show that the function defined by
Therefore, for any values of λ, f is continuous at x = 1
Question
19. Show that the function defined by
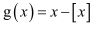 is discontinuous at all integral point. Here [denotes the greatest integer less than or equal to x.
Solution :
The given function is
is discontinuous at all integral point. Here [denotes the greatest integer less than or equal to x.
Solution :
The given function is
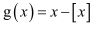 It is evident that g is defined at all integral points.
Let n be an integer.
Then,
It is evident that g is defined at all integral points.
Let n be an integer.
Then,
 It is observed that the left and right hand limits of f at x = n do not coincide.
Therefore, f is not continuous at x = n
Hence, g is discontinuous at all integral points.
Question
20. Is the function defined by
It is observed that the left and right hand limits of f at x = n do not coincide.
Therefore, f is not continuous at x = n
Hence, g is discontinuous at all integral points.
Question
20. Is the function defined by
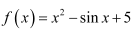 continuous at x = π ?
Solution :
The given function is
continuous at x = π ?
Solution :
The given function is
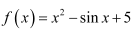 It is evident that f is defined at x = π
It is evident that f is defined at x = π
 Therefore, the given function f is continuous at x = π
Question 21. Discuss the continuity of the following functions.
(a) f (x) = sin x + cos x
(b) f (x) = sin x − cos x
(c) f (x) = sin x × cos x
Solution :
It is known that if g and h are two continuous functions, then
g + h, g - h and g.h are also continuous.
It has to proved first that g (x) = sin x and h (x) = cos x are continuous functions.
Let g (x) = sin x
It is evident that g (x) = sin x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
Therefore, the given function f is continuous at x = π
Question 21. Discuss the continuity of the following functions.
(a) f (x) = sin x + cos x
(b) f (x) = sin x − cos x
(c) f (x) = sin x × cos x
Solution :
It is known that if g and h are two continuous functions, then
g + h, g - h and g.h are also continuous.
It has to proved first that g (x) = sin x and h (x) = cos x are continuous functions.
Let g (x) = sin x
It is evident that g (x) = sin x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
 Therefore, g is a continuous function.
Let h (x) = cos x
It is evident that h (x) = cos x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
h (c) = cos c
Therefore, g is a continuous function.
Let h (x) = cos x
It is evident that h (x) = cos x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
h (c) = cos c
 Therefore, h is a continuous function.
Therefore, it can be concluded that
(a) f (x) = g (x) + h (x) = sin x + cos x is a continuous function
(b) f (x) = g (x) − h (x) = sin x − cos x is a continuous function
(c) f (x) = g (x) × h (x) = sin x × cos x is a continuous function
Question
22. Discuss the continuity of the cosine, cosecant, secant and cotangent functions,
Solution :
It is known that if g and h are two continuous functions, then
It has to be proved first that g (x) = sin x and h (x) = cos x are continuous functions.
Let g (x) = sin x
It is evident that g (x) = sin x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
Therefore, h is a continuous function.
Therefore, it can be concluded that
(a) f (x) = g (x) + h (x) = sin x + cos x is a continuous function
(b) f (x) = g (x) − h (x) = sin x − cos x is a continuous function
(c) f (x) = g (x) × h (x) = sin x × cos x is a continuous function
Question
22. Discuss the continuity of the cosine, cosecant, secant and cotangent functions,
Solution :
It is known that if g and h are two continuous functions, then
It has to be proved first that g (x) = sin x and h (x) = cos x are continuous functions.
Let g (x) = sin x
It is evident that g (x) = sin x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
 Therefore, g is a continuous function.
Let h (x) = cos x
It is evident that h (x) = cos x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
h (c) = cos c
Therefore, g is a continuous function.
Let h (x) = cos x
It is evident that h (x) = cos x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
h (c) = cos c
 Therefore, h (x) = cos x is continuous function.
It can be concluded that,
Therefore, h (x) = cos x is continuous function.
It can be concluded that,
 Question
23. Find the points of discontinuity of f, where
Question
23. Find the points of discontinuity of f, where
 Solution :
The given function f is
Solution :
The given function f is
 It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
 Therefore, f is continuous at x = 0
From the above observations, it can be concluded that f is continuous at all points of the real line.
Thus, f has no point of discontinuity.
Question
24. Determine if f defined by
Therefore, f is continuous at x = 0
From the above observations, it can be concluded that f is continuous at all points of the real line.
Thus, f has no point of discontinuity.
Question
24. Determine if f defined by
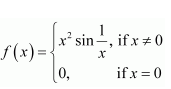 is a continuous function?
Solution :
The given function f is
is a continuous function?
Solution :
The given function f is
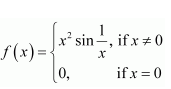 It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
 Therefore, f is continuous at x = 0
From the above observations, it can be concluded that f is continuous at every point of the real line.
Thus, f is a continuous function.
Question
25. Examine the continuity of f, where f is defined by
Therefore, f is continuous at x = 0
From the above observations, it can be concluded that f is continuous at every point of the real line.
Thus, f is a continuous function.
Question
25. Examine the continuity of f, where f is defined by
 Solution :
The given function f is
Solution :
The given function f is
 It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
 Therefore, f is continuous at x = 0
From the above observations, it can be concluded that f is continuous at every point of the real line.
Thus, f is a continuous function.
Question
26. Find the values of k so that the function f is continuous at the indicated point.
Therefore, f is continuous at x = 0
From the above observations, it can be concluded that f is continuous at every point of the real line.
Thus, f is a continuous function.
Question
26. Find the values of k so that the function f is continuous at the indicated point.
 Solution :
The given function f is
Solution :
The given function f is
 The given function f is continuous at x = π/2 , if f is defined at x = π/2 and if the value of the f at x = π/2 equals the limit of f at x = π/2 .
It is evident that f is defined at x = π/2 and f( π/2) = 3
The given function f is continuous at x = π/2 , if f is defined at x = π/2 and if the value of the f at x = π/2 equals the limit of f at x = π/2 .
It is evident that f is defined at x = π/2 and f( π/2) = 3
 Therefore, the required value of k is 6.
Question
27. Find the values of k so that the function f is continuous at the indicated point.
Therefore, the required value of k is 6.
Question
27. Find the values of k so that the function f is continuous at the indicated point.
 Solution :
The given function is
Solution :
The given function is
 The given function f is continuous at x = 2, if f is defined at x = 2 and if the value of f at x = 2 equals the limit of f at x = 2
It is evident that f is defined at x = 2 and f(2) = k(2)
2
= 4k
The given function f is continuous at x = 2, if f is defined at x = 2 and if the value of f at x = 2 equals the limit of f at x = 2
It is evident that f is defined at x = 2 and f(2) = k(2)
2
= 4k
 Therefore, the required value of k is 3/4.
Question
28. Find the values of k so that the function f is continuous at the indicated point.
Therefore, the required value of k is 3/4.
Question
28. Find the values of k so that the function f is continuous at the indicated point.
 Solution :
The given function is
Solution :
The given function is
 The given function f is continuous at x = p, if f is defined at x = p and if the value of f at x = p equals the limit of f at x = p
It is evident that f is defined at x = p and f(π) = kπ + 1
The given function f is continuous at x = p, if f is defined at x = p and if the value of f at x = p equals the limit of f at x = p
It is evident that f is defined at x = p and f(π) = kπ + 1
 Therefore, the required value of k is -2/π
Question
29. Find the values of k so that the function f is continuous at the indicated point.
Therefore, the required value of k is -2/π
Question
29. Find the values of k so that the function f is continuous at the indicated point.
 Solution :
The given function f is
Solution :
The given function f is
 The given function f is continuous at x = 5, if f is defined at x = 5 and if the value of f at x = 5 equals the limit of f at x = 5
It is evident that f is defined at x = 5 and f(5) = kx + 1 = 5k + 1
The given function f is continuous at x = 5, if f is defined at x = 5 and if the value of f at x = 5 equals the limit of f at x = 5
It is evident that f is defined at x = 5 and f(5) = kx + 1 = 5k + 1
 Therefore, the required value of k is 9/5
Question
30. Find the values of a and b such that the function defined by
Therefore, the required value of k is 9/5
Question
30. Find the values of a and b such that the function defined by
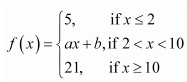 is a continuous function.
Solution :
The given function f is
is a continuous function.
Solution :
The given function f is
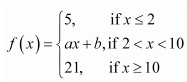 It is evident that the given function f is defined at all points of the real line.
If f is a continuous function, then f is continuous at all real numbers.
In particular, f is continuous at x = 2 and x = 10
Since f is continuous at x = 2, we obtain
It is evident that the given function f is defined at all points of the real line.
If f is a continuous function, then f is continuous at all real numbers.
In particular, f is continuous at x = 2 and x = 10
Since f is continuous at x = 2, we obtain
 Therefore, the values of a and b for which f is a continuous function are 2 and 1 respectively.
Question
31. Show that the function defined by f (x) = cos (x
2
) is a continuous function.
Solution :
The given function is f (x) = cos (x
2
)
This function f is defined for every real number and f can be written as the composition of two functions as,
f = g o h, where g (x) = cos x and h (x) = x
2
Therefore, the values of a and b for which f is a continuous function are 2 and 1 respectively.
Question
31. Show that the function defined by f (x) = cos (x
2
) is a continuous function.
Solution :
The given function is f (x) = cos (x
2
)
This function f is defined for every real number and f can be written as the composition of two functions as,
f = g o h, where g (x) = cos x and h (x) = x
2
 It has to be first proved that g (x) = cos x and h (x) = x
2
are continuous functions.
It is evident that g is defined for every real number.
Let c be a real number.
Then, g (c) = cos c
It has to be first proved that g (x) = cos x and h (x) = x
2
are continuous functions.
It is evident that g is defined for every real number.
Let c be a real number.
Then, g (c) = cos c
 Therefore, g (x) = cos x is continuous function.
h (x) = x
2
Clearly, h is defined for every real number.
Let k be a real number, then h (k) = k
2
Therefore, g (x) = cos x is continuous function.
h (x) = x
2
Clearly, h is defined for every real number.
Let k be a real number, then h (k) = k
2
 Therefore, h is a continuous function.
It is known that for real valued functions g and h,such that (g o h) is defined at c, if g is continuous at c and if f is continuous at g (c), then (f o g) is continuous at c.
Therefore, h is a continuous function.
Question
32. Show that the function defined by f(x) = |cos x| is a continuous function.
Solution :
The given function is f(x) = |cos x|
This function f is defined for every real number and f can be written as the composition of two functions as,
f = g o h, where g(x) = |x| and h(x) = cos x
Therefore, h is a continuous function.
It is known that for real valued functions g and h,such that (g o h) is defined at c, if g is continuous at c and if f is continuous at g (c), then (f o g) is continuous at c.
Therefore, h is a continuous function.
Question
32. Show that the function defined by f(x) = |cos x| is a continuous function.
Solution :
The given function is f(x) = |cos x|
This function f is defined for every real number and f can be written as the composition of two functions as,
f = g o h, where g(x) = |x| and h(x) = cos x
 It has to be first proved that g(x) = |x| and h(x) = cos x are continuous functions.
It has to be first proved that g(x) = |x| and h(x) = cos x are continuous functions.
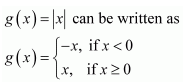 Clearly, g is defined for all real numbers.
Let c be a real number.
Case I:
Clearly, g is defined for all real numbers.
Let c be a real number.
Case I:
 Therefore, g is continuous at all points x, such that x < 0
Case II:
Therefore, g is continuous at all points x, such that x < 0
Case II:
 Therefore, g is continuous at all points x, such that x > 0
Case III:
Therefore, g is continuous at all points x, such that x > 0
Case III:
 Therefore, g is continuous at x = 0
From the above three observations, it can be concluded that g is continuous at all points.
h (x) = cos x
It is evident that h (x) = cos x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
h (c) = cos c
Therefore, g is continuous at x = 0
From the above three observations, it can be concluded that g is continuous at all points.
h (x) = cos x
It is evident that h (x) = cos x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
h (c) = cos c
 Therefore, h (x) = cos x is a continuous function.
It is known that for real valued functions g and h,such that (g o h) is defined at c, if g is continuous at c and if f is continuous at g (c), then (f o g) is continuous at c.
Therefore,
Therefore, h (x) = cos x is a continuous function.
It is known that for real valued functions g and h,such that (g o h) is defined at c, if g is continuous at c and if f is continuous at g (c), then (f o g) is continuous at c.
Therefore,
 is a continuous function.
Question
33. Examine that sin|x| is a continuous function.
Solution :
Let, f(x) = sin|x|
This function f is defined for every real number and f can be written as the composition of two functions as,
f = g o h, where g (x) = |x| and h (x) = sin x
is a continuous function.
Question
33. Examine that sin|x| is a continuous function.
Solution :
Let, f(x) = sin|x|
This function f is defined for every real number and f can be written as the composition of two functions as,
f = g o h, where g (x) = |x| and h (x) = sin x
 It has to be proved first that g (x) = |x| and h (x) = sin x are continuous functions.
It has to be proved first that g (x) = |x| and h (x) = sin x are continuous functions.
 Clearly, g is defined for all real numbers.
Let c be a real number.
Case I:
Clearly, g is defined for all real numbers.
Let c be a real number.
Case I:
.png) Therefore, g is continuous at all points x, such that x < 0
Case II:
Therefore, g is continuous at all points x, such that x < 0
Case II:
.png) Therefore, g is continuous at all points x, such that x > 0
Case III:
Therefore, g is continuous at all points x, such that x > 0
Case III:
 Therefore, g is continuous at x = 0
From the above three observations, it can be concluded that g is continuous at all points.
h (x) = sin x
It is evident that h (x) = sin x is defined for every real number.
Let c be a real number. Put x = c + k
If x → c, then k → 0
h (c) = sin c
Therefore, g is continuous at x = 0
From the above three observations, it can be concluded that g is continuous at all points.
h (x) = sin x
It is evident that h (x) = sin x is defined for every real number.
Let c be a real number. Put x = c + k
If x → c, then k → 0
h (c) = sin c
 Therefore, h is a continuous function.
It is known that for real valued functions g and h,such that (g o h) is defined at c, if g is continuous at c and if f is continuous at g (c), then (f o g) is continuous at c.
Therefore,
Therefore, h is a continuous function.
It is known that for real valued functions g and h,such that (g o h) is defined at c, if g is continuous at c and if f is continuous at g (c), then (f o g) is continuous at c.
Therefore,
 is a continuous function.
Question
34. Find all the points of discontinuity of f defined by
f(x) = |x| - |x + 1|.
Solution :
The given function is f(x) = |x| - |x + 1|
The two functions, g and h, are defined as
is a continuous function.
Question
34. Find all the points of discontinuity of f defined by
f(x) = |x| - |x + 1|.
Solution :
The given function is f(x) = |x| - |x + 1|
The two functions, g and h, are defined as

 Therefore, h is continuous at x = −1
From the above three observations, it can be concluded that h is continuous at all points of the real line.
g and h are continuous functions. Therefore, f = g − h is also a continuous function.
Therefore, f has no point of discontinuity.
Therefore, h is continuous at x = −1
From the above three observations, it can be concluded that h is continuous at all points of the real line.
g and h are continuous functions. Therefore, f = g − h is also a continuous function.
Therefore, f has no point of discontinuity.
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.1 FAQs
What are the conditions for continuity and differentiability?
What are the 3 conditions of continuity?
What is the SI unit of equation of continuity?
What is the concept of continuity?
Is continuity necessary for integration?










