NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.3 - Continuity and Differentiability
NCERT Solutions for Class 12 Maths Chapter 5 Miscellaneous Exercise: This page Consist of detail step by step NCERT Solutions For Class 12 Maths Chapter 5-Continuity and Differentiability miscellaneous exercise.
Krati Saraswat6 Aug, 2024
Share
NCERT Solutions for Class 12 Maths Chapter 5 Miscellaneous Exercise (Continuity and Differentiability)
NCERT Solutions for Class 12 Maths Chapter 5 Miscellaneous Exercise of Continuity and Differentiability is prepared by academic team of pw. We have prepared NCERT Solutions for all exercise of chapter-5. Given below is step by step solutions of all questions given in NCERT Solutions for Class 12 Maths Chapter 5 Miscellaneous Exercise of Continuity and Differentiability.NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.1
NCERT Solutions for Class 12 Maths Chapter 5 Miscellaneous Exercise Overview
These crucial subjects are covered in NCERT Solutions for Class 12 Maths Chapter 5. In order to completely comprehend the concepts presented in the chapter and make the best use of the offered answers, students are recommended to go over each topic in great detail. The Physics Wallah teachers have been working hard to help students comprehend the concepts discussed in this chapter, and the results are these solutions. Students should easily achieve excellent exam outcomes after reviewing and practicing these solutions.NCERT Solutions for Class 12 Maths Chapter 5 Miscellaneous Exercise PDF
Our team of teachers at Physics Wallah has developed thorough solutions for NCERT Solutions for Class 12 Maths Chapter 5 in order to help students understand and apply chapter concepts. The purpose of these questions is to help students comprehend explanations. You may obtain the NCERT Solutions for Class 12 Maths, Chapter 5 PDF by clicking on this link:NCERT Solutions Class 12 Maths Chapter 5 PDF Download Link
NCERT Solutions for Class 12 Maths Chapter 5 Miscellaneous Exercise
Solve The Following Questions of NCERT Solutions for Class 12 Maths Chapter 5 Miscellaneous Exercise of Continuity and Differentiability:
Question 1.
Solution : Let Using chain rule, we obtain 
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.2
Question 2.
Solution : Let 
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.3
Question 3 .
Solution : Let, Taking logarithm on both the sides, we obtain log y = 3 cos 2x log(5x) Differentiating both sides with respect to x, we obtain 
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.4
Question 4.
Solution : Let, Using chain rule, we obtain 
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.5
Question 5.
Solution : Let y = 
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.6
Question 6 .
Solution : Let ,y = .......(1) 
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.7
Question 7.
Solution : Let, y = Taking logarithm on both the sides, we obtain log y = log x. log (log x) Differentiating both sides with respect to x, we obtain 
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.8
Question 8 . Differentiate w.r.t. x the function cos (a cos x + b sin x), for some constant a and b. Solution : Let, y = cos (a cos x + b sin x) By using chain rule, we obtain
Question 9.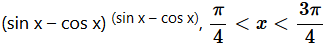 
Solution : Let, y = 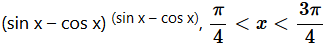Taking logarithm on both the sides, we obtain 
Question 10. 
, for some fixed a> 0 and x > 0 Solution : Let y = 
Since a is constant, aa is also a constant. ∴ ds/dx = 0 .....(5) From (1), (2), (3), (4), and (5), we obtain 
Question 11. 
, for x > 3 Solution : 
Question 12. Find dy/dx , if .png)
Solution : 
Question 1 3. Find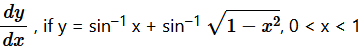 
Solution : 
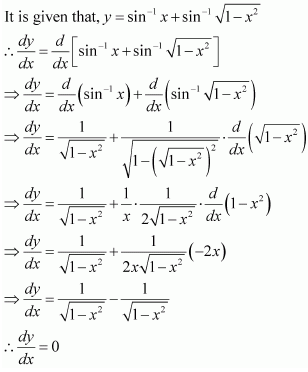Question 14. If 
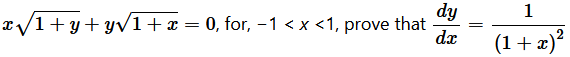Solution : It is given that, 
Differentiating both sides with respect to x, we obtain 
Hence, proved. Question 15. 
Solution : It is given that, 
Differentiating both sides with respect to x, we obtain 
= - c which is constant and independent of a and b Hence, proved. Question 16. If cos y = x cos (a + y), with cos a ≠ ± 1, prove that prove that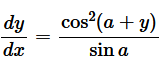 
Solution : It is given cos y = x cos (a + y) 
Hence, proved. Question 17. If x = a (cos t + t sin t) and y = a (sin t – t cos t), find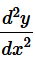 
Solution : It is given that, x = a(cost + tsin t) and y = a (sin t - t cost) 
Question 18. If f (x) = |x| 3 show that f''(x) exists for all real x, and find it. Solution : It is known that, 
Therefore, when x ≥ 0, f(x) = |x| 3 = x 3 In this case, f'(x) = 3x 2 and hence, f''(x) = 6x When x < 0, f(x) = |x| 3 = (-x 3 ) = -x 3 In this case, f'(x) = -3x 2 and hence, f''(x) = -6x Thus, for f(x) = |x| 3 , f''(x) exists for all real x and is given by, 
Question 19. Using mathematical induction prove that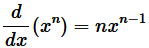 
for all positive integers n. Solution : 
For n = 1, 
∴P(n) is true for n = 1 Let P(k) is true for some positive integer k. That is,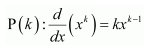 
It has to be proved that P(k + 1) is also true. 
Thus, P(k + 1) is true whenever P (k) is true. Therefore, by the principle of mathematical induction, the statement P(n) is true for every positive integer n. Hence, proved. Question 20. Using the fact that sin (A + B) = sin A cos B + cos A sin B and the differentiation, obtain the sum formula for cosines. Solution : sin (A + B) = sin A cos B + cos A sin B Differentiating both sides with respect to x, we obtain 
Question 21. Does there exist a function which is continuos everywhere but not differentiable at exactly two points? Justify your answer ? Solution : y={|x| −∞< x ≤ 1 2−x 1≤ x ≤ ∞ 
It can be seen from the above graph that, the given function is continuos everywhere but not differentiable at exactly two points which are 0 and 1. Question 22. If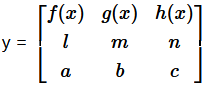 
, prove that 
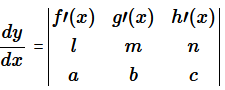Solution : 
Question 23. If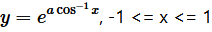 
, show that 
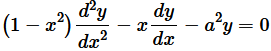Solution : It is given that, 
NCERT Solutions for Class 12 Maths Chapter 5 FAQs
What is the relationship between continuity and differentiability?
The relationship between continuous functions and differentiability is- all differentiable functions are continuous but not all continuous functions are differentiable.
What is important in continuity and differentiability class 12?
In continuity and differentiability class 12, we will learn important concepts of differentiability, continuity, and relationship between them.
What are the properties of continuity and differentiability?
Continuity of a function is the characteristic of a function by virtue of which, the graphical form of that function is a continuous wave. A differentiable function is a function whose derivative exists at each point in its domain.
What is the use of continuity in real life?
The water flow in the rivers is continuous. The flow of time in human life is continuous i.e. you are getting older continuously. And so on. Similarly, in mathematics, we have the notion of the continuity of a function.
Is continuity sufficient for differentiability?
In particular, any differentiable function must be continuous at every point in its domain. The converse does not hold: a continuous function need not be differentiable.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.