
NCERT Solutions For Class 12 Maths Chapter 5 Exercise 5.5 Continuity and Differentiability
NCERT Solutions For Class 12 Maths Chapter 5 Exercise 5.5 Continuity and Differentiability is prepared by the academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of Chapter 5. Given below is step by step solutions of all questions given in NCERT Solutions For Class 12 Maths Chapter 5 Exercise 5.5 Continuity and Differentiability.NCERT Solutions for Class 12 Maths Chapter 5 Miscellaneous Exercise
NCERT Solutions For Class 12 Maths Chapter 5 Exercise 5.5 Overview
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.5 addresses these significant subjects. In order to fully comprehend the concepts presented in the chapter and make effective use of the provided solutions, it is recommended that students go over each topic in great detail. The intention is for students to effortlessly achieve excellent exam scores after reviewing and practicing these responses.NCERT Solutions For Class 12 Maths Chapter 5 Exercise 5.5
Solve The Following Questions NCERT Solutions For Class 12 Maths Chapter 5 Exercise 5.5 Continuity and Differentiability
Question 1. Differentiate the function with respect to x.cos x.cos 2x.cos3x
Solution : Let y = cos x.cos 2x.cos3x Taking logarithm on both the sides, we obtain
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.1
Question 2. Differentiate the function with respect to x. Solution :
Let y =
Solution :
Let y =
 Taking logarithm on both the sides, we obtain
Taking logarithm on both the sides, we obtain

NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.2
Question 3. Differentiate the function with respect to x. Solution :
Let, y =
Solution :
Let, y =
 Taking logarithm on both the sides, we obtain
log y = cos x .log(log x)
Differentiating both sides with respect to x, we obtain
Taking logarithm on both the sides, we obtain
log y = cos x .log(log x)
Differentiating both sides with respect to x, we obtain

NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.3
Question 4. Differentiate the function with respect to x. Solution :
Solution :

NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.4
Question 5. Differentiate the function with respect to x. Solution :
Solution :

NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.6
Question 6. Differentiate the function with respect to x. Solution :
Solution :
 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain

NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.7
Question 7. Differentiate the function with respect to x. Solution :
Solution :
 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain

NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.8
Question 8. Differentiate the function with respect to x. Solution :
Solution :
 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain

 Question
9. Differentiate the function with respect to x.
Question
9. Differentiate the function with respect to x.
 Solution :
Let, y =
Solution :
Let, y =

 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
 Question
10. Differentiate the function with respect to x.
Question
10. Differentiate the function with respect to x.
 Solution :
Let, y =
Solution :
Let, y =

 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
 Question
11. Differentiate the function with respect to x.
Question
11. Differentiate the function with respect to x.
 Solution :
Let, y =
Solution :
Let, y =

 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
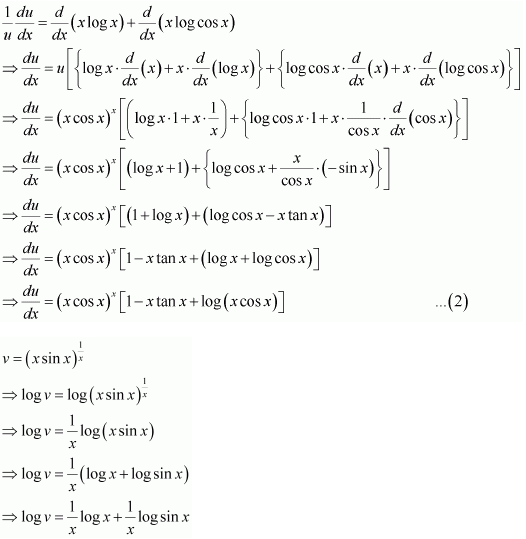 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
 Question
12. Find dy/dx of function.
x
y
+ y
x
= 1
Solution :
The given function is x
y
+ y
x
= 1
Let x
y
= u and y
x
= v
Then, the function becomes u + v = 1
∴du/dx + dv/dx = 1
Question
12. Find dy/dx of function.
x
y
+ y
x
= 1
Solution :
The given function is x
y
+ y
x
= 1
Let x
y
= u and y
x
= v
Then, the function becomes u + v = 1
∴du/dx + dv/dx = 1
 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
 Question
13. Find dy/dx of function.
y
x
= x
y
Solution :
The given function is y
x
= x
y
Taking logarithm on both the sides, we obtain
x log y = y log x
Differentiating both sides with respect to x, we obtain
Question
13. Find dy/dx of function.
y
x
= x
y
Solution :
The given function is y
x
= x
y
Taking logarithm on both the sides, we obtain
x log y = y log x
Differentiating both sides with respect to x, we obtain
 Question
14. Find dy/dx of function.
Question
14. Find dy/dx of function.
(cos x) y = (cos y) x
Solution : The given function is (cos x) y = (cos y) x Taking logarithm on both the sides, we obtain y log cos x = x log cos y Differentiating both sides, we obtain Question
15. Find dy/dx of function.
Question
15. Find dy/dx of function.
xy = e (x-y)
Solution : The given function is xy = e (x-y) Taking logarithm on both the sides, we obtain log(xy) = log(e (x-y) ) Differentiating both sides with respect to x, we obtain Question
16. Find the derivative of the function given by
Question
16. Find the derivative of the function given by
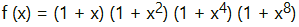 and hence find f'(1)
Solution :
The given relationship is
and hence find f'(1)
Solution :
The given relationship is
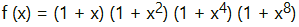 Taking logarithm on both the sides, we obtain
Taking logarithm on both the sides, we obtain
 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
 Question
17. Differentiate
Question
17. Differentiate
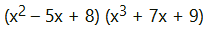 in three ways mentioned below
(i) By using product rule.
(ii) By expanding the product to obtain a single polynomial.
(iii By logarithmic differentiation.
Do they all give the same answer?
Solution :
Let, y =
in three ways mentioned below
(i) By using product rule.
(ii) By expanding the product to obtain a single polynomial.
(iii By logarithmic differentiation.
Do they all give the same answer?
Solution :
Let, y =
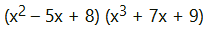 (i)
(i)
 (ii)
(ii)
 (iii) y =
(iii) y =
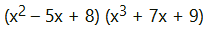 Taking logarithm on both the sides, we obtain
Taking logarithm on both the sides, we obtain
 Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
 From the above three observations, it can be concluded that all the results of dy/dx are same.
Question
18. If u, v and w are functions of x, then show that
From the above three observations, it can be concluded that all the results of dy/dx are same.
Question
18. If u, v and w are functions of x, then show that
 in two ways-first by repeated application of product rule, second by logarithmic differentiation.
Solution :
Let y = u.v.w = u(v.w)
By applying product rule, we obtain
in two ways-first by repeated application of product rule, second by logarithmic differentiation.
Solution :
Let y = u.v.w = u(v.w)
By applying product rule, we obtain
 By taking logarithm on both sides of the equation y = u.v.w, we obtain
log y = log u + log v + log w
Differentiating both sides with respect to x, we obtain
By taking logarithm on both sides of the equation y = u.v.w, we obtain
log y = log u + log v + log w
Differentiating both sides with respect to x, we obtain

NCERT Solutions For Class 12 Maths Chapter 5 Exercise 5.5 FAQs
What is continuity in math class 12?
What is a continuous and differentiable function Class 12?
How many exercises are there in chapter 5 class 12 maths?
What is the principle of continuity in math?
What functions are not continuous?










