
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.8 Continuity and Differentiability
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.8 Continuity and Differentiability is prepared by the academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of Chapter 5. Given below is step by step solutions to all questions given in NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.8 Continuity and Differentiability.NCERT Solutions for Class 12 Maths Chapter 5 Miscellaneous Exercise
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.8 Overview
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.8 covers these important topics. Students are encouraged to review each topic thoroughly in order to fully understand the concepts taught in the chapter and make optimal use of the provided solutions. These solutions are the outcome of the dedicated effort that the Physics Wallah teachers have been doing to aid students in understanding the ideas covered in this chapter. After going over and rehearsing these responses, the goal is for students to easily score outstanding exam results.NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.8
Solve The Following Questions NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.8 Continuity and Differentiability
Question 1.Verify Rolle’s Theorem for the function f(x) = x 2 + 2x – 8, x ∈ [– 4, 2]. Solution : The given function,f(x) = x 2 + 2x – 8 being a polynomial function, is continuous in [−4, 2] and is differentiable in (−4, 2). ∴ f (−4) = f (2) = 0
⇒ The value of f (x) at −4 and 2 coincides.
Rolle’s Theorem states that there is a point c ∈ (−4, 2) such that f'(c) = 0
∴ f (−4) = f (2) = 0
⇒ The value of f (x) at −4 and 2 coincides.
Rolle’s Theorem states that there is a point c ∈ (−4, 2) such that f'(c) = 0
 Hence, Rolle’s Theorem is verified for the given function.
Hence, Rolle’s Theorem is verified for the given function.
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.1
Question 2. Examine if Rolle’s Theorem is applicable to any of the following functions. Can you say some thing about the converse of Rolle’s Theorem from these examples? (i)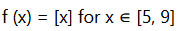 (ii)
(ii)
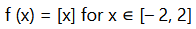 (iii)
(iii)
 Solution :
By Rolle’s Theorem, for a function f[a,b] →R, if
(a) f is continuous on [a, b]
(b) f is differentiable on (a, b)
(c) f (a) = f (b)
then, there exists some c ∈ (a, b) such that f'(c) = 0
Therefore, Rolle’s Theorem is not applicable to those functions that do not satisfy any of the three conditions of the hypothesis.
(i)
Solution :
By Rolle’s Theorem, for a function f[a,b] →R, if
(a) f is continuous on [a, b]
(b) f is differentiable on (a, b)
(c) f (a) = f (b)
then, there exists some c ∈ (a, b) such that f'(c) = 0
Therefore, Rolle’s Theorem is not applicable to those functions that do not satisfy any of the three conditions of the hypothesis.
(i)
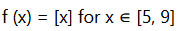 It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = 5 and x = 9
⇒ f (x) is not continuous in [5, 9].
Also, f(5) = [5] = 5 and f(9) = [9] = 9
∴ f(5) ≠ f(9)
The differentiability of f in (5, 9) is checked as follows.
Let n be an integer such that n ∈ (5, 9).
It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = 5 and x = 9
⇒ f (x) is not continuous in [5, 9].
Also, f(5) = [5] = 5 and f(9) = [9] = 9
∴ f(5) ≠ f(9)
The differentiability of f in (5, 9) is checked as follows.
Let n be an integer such that n ∈ (5, 9).
 Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴f is not differentiable in (5, 9).
It is observed that f does not satisfy all the conditions of the hypothesis of Rolle’s Theorem.
Hence, Rolle’s Theorem is not applicable for
Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴f is not differentiable in (5, 9).
It is observed that f does not satisfy all the conditions of the hypothesis of Rolle’s Theorem.
Hence, Rolle’s Theorem is not applicable for
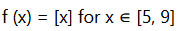 (ii)
(ii)
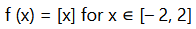 It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = −2 and x = 2
⇒ f (x) is not continuous in [−2, 2].
Also, f(-2) = [-2] = -2 and f(2) = [2] = 2
∴ f(-2) ≠ f(2)
The differentiability of f in (−2, 2) is checked as follows.
Let n be an integer such that n ∈ (−2, 2).
It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = −2 and x = 2
⇒ f (x) is not continuous in [−2, 2].
Also, f(-2) = [-2] = -2 and f(2) = [2] = 2
∴ f(-2) ≠ f(2)
The differentiability of f in (−2, 2) is checked as follows.
Let n be an integer such that n ∈ (−2, 2).
 Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴f is not differentiable in (−2, 2).
It is observed that f does not satisfy all the conditions of the hypothesis of Rolle’s Theorem.
Hence, Rolle’s Theorem is not applicable for
.
Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴f is not differentiable in (−2, 2).
It is observed that f does not satisfy all the conditions of the hypothesis of Rolle’s Theorem.
Hence, Rolle’s Theorem is not applicable for
.
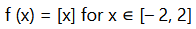 (iii)
(iii)
 It is evident that f, being a polynomial function, is continuous in [1, 2] and is differentiable in (1, 2).
f(1) = 1
2
- 1 = 0
f(2) = 2
2
- 1 = 3
∴f (1) ≠ f (2)
It is observed that f does not satisfy a condition of the hypothesis of Rolle’s Theorem.
Hence, Rolle’s Theorem is not applicable for .
It is evident that f, being a polynomial function, is continuous in [1, 2] and is differentiable in (1, 2).
f(1) = 1
2
- 1 = 0
f(2) = 2
2
- 1 = 3
∴f (1) ≠ f (2)
It is observed that f does not satisfy a condition of the hypothesis of Rolle’s Theorem.
Hence, Rolle’s Theorem is not applicable for .

NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.2
Question 3. If f:[-5,5] →R is a differentiable function and if f'(x) does not vanish anywhere, then prove that f(-5) ≠ f(5). Solution : It is given that f:[-5,5] →R is a differentiable function. Since every differentiable function is a continuous function, we obtain (a) f is continuous on [−5, 5]. (b) f is differentiable on (−5, 5). Therefore, by the Mean Value Theorem, there exists c ∈ (−5, 5) such that It is also given that f'(x) does not vanish anywhere.
It is also given that f'(x) does not vanish anywhere.
 Hence, proved.
Hence, proved.
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.3
Question 4. Verify Mean Value Theorem, if f(x) = x 2 - 4x - 3 in the interval [a,b], where a = 1 and b = 4. Solution : The given function is f(x) = x 2 - 4x - 3 f, being a polynomial function, is continuous in [1, 4] and is differentiable in (1, 4) whose derivative is 2x − 4. Mean Value Theorem states that there is a point c ∈ (1, 4) such that f'(c) = 1
Mean Value Theorem states that there is a point c ∈ (1, 4) such that f'(c) = 1
 Hence, Mean Value Theorem is verified for the given function.
Hence, Mean Value Theorem is verified for the given function.
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.4
Question 5. Verify Mean Value Theorem, if f(x) = x 3 - 5x 2 - 3x in the interval [a, b], where a = 1 and b = 3. Find all c ∈ (1, 3) for which f'(c) = 0 Solution : The given function f is f(x) = x 3 - 5x 2 - 3x f, being a polynomial function, is continuous in [1, 3] and is differentiable in (1, 3) whose derivative is 3x2 − 10x − 3. Mean Value Theorem states that there exist a point c ∈ (1, 3) such that f'(c) = - 10
Mean Value Theorem states that there exist a point c ∈ (1, 3) such that f'(c) = - 10
 Hence, Mean Value Theorem is verified for the given function and c = 7/3 ∈ (1,3) is the only point for which f'(c) = 0
Hence, Mean Value Theorem is verified for the given function and c = 7/3 ∈ (1,3) is the only point for which f'(c) = 0
NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.5
Question 6. Examine the applicability of Mean Value Theorem for all three functions given in the above exercise 2. Solution : Mean Value Theorem states that for a function f[a,b] →R, if (a) f is continuous on [a, b] (b) f is differentiable on (a, b) then, there exists some c ∈ (a, b) such that Therefore, Mean Value Theorem is not applicable to those functions that do not satisfy any of the two conditions of the hypothesis.
(i)
Therefore, Mean Value Theorem is not applicable to those functions that do not satisfy any of the two conditions of the hypothesis.
(i)
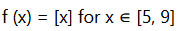 It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = 5 and x = 9
⇒ f (x) is not continuous in [5, 9].
The differentiability of f in (5, 9) is checked as follows.
Let n be an integer such that n ∈ (5, 9).
It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = 5 and x = 9
⇒ f (x) is not continuous in [5, 9].
The differentiability of f in (5, 9) is checked as follows.
Let n be an integer such that n ∈ (5, 9).
 Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴f is not differentiable in (5, 9).
It is observed that f does not satisfy all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is not applicable for
.
Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴f is not differentiable in (5, 9).
It is observed that f does not satisfy all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is not applicable for
.
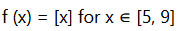 (ii)
(ii)
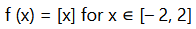 It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = −2 and x = 2
⇒ f (x) is not continuous in [−2, 2].
The differentiability of f in (−2, 2) is checked as follows.
Let n be an integer such that n ∈ (−2, 2).
It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = −2 and x = 2
⇒ f (x) is not continuous in [−2, 2].
The differentiability of f in (−2, 2) is checked as follows.
Let n be an integer such that n ∈ (−2, 2).
 Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴f is not differentiable in (−2, 2).
It is observed that f does not satisfy all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is not applicable for
Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴f is not differentiable in (−2, 2).
It is observed that f does not satisfy all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is not applicable for
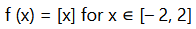 (iii)
(iii)
 It is evident that f, being a polynomial function, is continuous in [1, 2] and is differentiable in (1, 2).
It is observed that f satisfies all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is applicable for
It is evident that f, being a polynomial function, is continuous in [1, 2] and is differentiable in (1, 2).
It is observed that f satisfies all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is applicable for
 It can be proved as follows.
It can be proved as follows.

NCERT Solutions for Class 12 Maths Chapter 5 Exercise 5.8 FAQs
In which chapter is Rolle's theorem?
Rolle's theorem is a special case of the mean-value theorem in differential calculus. NCERT solutions class 12 maths Chapter 5 Exercise 5.8 has 6 questions based on these theorems and their applications.
What is a continuous and differentiable function Class 12?
Continuity of a function is the characteristic of a function by virtue of which, the graphical form of that function is a continuous wave. A differentiable function is a function whose derivative exists at each point in its domain.
Why do we use Rolle's theorem?
Rolle's theorem is favored for remarking on the existence of stationary points for a continuous and derivable function with known roots. We learned to solve issues by applying Rolle's theorem, which we learned to prove through examples.
What is continuity at a number?
A function is said to be continuous if it can be drawn without picking up the pencil. Otherwise, a function is said to be discontinuous. Similarly, Calculus in Maths, a function f(x) is continuous at x = c, if there is no break in the graph of the given function at the point. (c, f(c)).
What is the difference between continuity and differentiation?
Continuity of a function is the characteristic of a function by virtue of which, the graphical form of that function is a continuous wave. A differentiable function is a function whose derivative exists at each point in its domain.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.









