
NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.4 (Differential Equations)
NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.4 Differential Equations is prepared by the academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of Chapter 9. Given below is step by step solutions to all questions given in the NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.4 Differential Equations.NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.4 Overview
NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.4 covers these important topics. Students are encouraged to review each topic thoroughly in order to fully understand the concepts taught in the chapter and make optimal use of the provided solutions. These solutions are the outcome of the dedicated effort that the Physics Wallah teachers have been doing to aid students in understanding the ideas covered in this chapter. After going over and rehearsing these responses, the goal is for students to easily score outstanding exam results.NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.4
Solve The Following Questions of NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.4: For each of the differential equations in Questions 1 to 4, find the general solution: Question 1.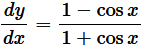 Solution : Given: Differential equation
Solution : Given: Differential equation 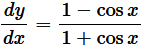
 This is the required general solution of the given differential equation. Question 2.
This is the required general solution of the given differential equation. Question 2.  Solution : The given differential equation is:
Solution : The given differential equation is:  This is the required general solution of the given differential equation. Question 3.
This is the required general solution of the given differential equation. Question 3.  Solution : Given: Differential equation
Solution : Given: Differential equation  This is the required general solution of the given differential equation. Question 4.
This is the required general solution of the given differential equation. Question 4.  Solution : Given: Differential equation
Solution : Given: Differential equation  This is the required general solution of the given differential equation.
This is the required general solution of the given differential equation.Question 5.
 Solution : Given: Differential equation
Solution : Given: Differential equation 
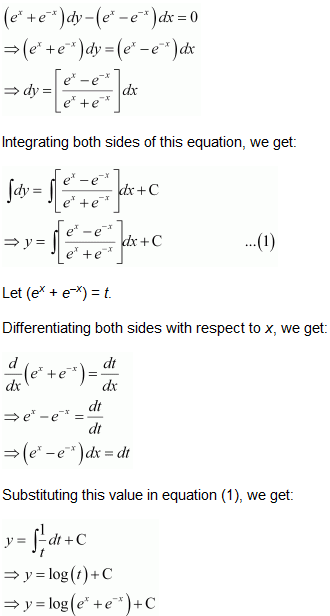 This is the required general solution of the given differential equation. Question 6.
This is the required general solution of the given differential equation. Question 6. 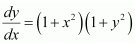 Solution : Given: Differential equation
Solution : Given: Differential equation 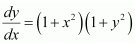
 Question 7. y log y dx – x dy = 0 Solution : Given: Differential equation y log y dx – x dy = 0
Question 7. y log y dx – x dy = 0 Solution : Given: Differential equation y log y dx – x dy = 0  This is the required general solution of the given differential equation. Question 8.
This is the required general solution of the given differential equation. Question 8.  Solution : Given: Differential equation
Solution : Given: Differential equation 
 Question 9.
Question 9.  Solution : Given: Differential equation
Solution : Given: Differential equation 
 This is the required general solution of the given differential equation. Question 10.
This is the required general solution of the given differential equation. Question 10.  Solution : Given: Differential equation
Solution : Given: Differential equation 
 For each of the differential equations in Question 11 to 12, find a particular solution satisfying the given condition: Question 11.
For each of the differential equations in Question 11 to 12, find a particular solution satisfying the given condition: Question 11. 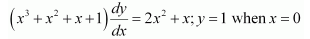 Solution :
Solution :  Comparing the coefficients of x 2 and x , we get: A + B = 2 B + C = 1 A + C = 0 Solving these equations, we get:
Comparing the coefficients of x 2 and x , we get: A + B = 2 B + C = 1 A + C = 0 Solving these equations, we get:  Question 12.
Question 12. 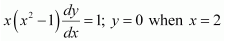 Solution :
Solution :  For each of the differential equations in Question 13 to 14, find a particular solution satisfying the given condition. Question 13.
For each of the differential equations in Question 13 to 14, find a particular solution satisfying the given condition. Question 13. 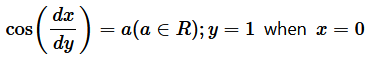 Solution :
Solution :  Question 14.
Question 14. 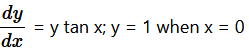 Solution :
Solution :  Substituting C = 1 in equation (1), we get: y = sec x Question 15. Find the equation of the curve passing through the point (0, 0) and whose differential equation is y' = e x sin x Solution : The differential equation of the curve is:
Substituting C = 1 in equation (1), we get: y = sec x Question 15. Find the equation of the curve passing through the point (0, 0) and whose differential equation is y' = e x sin x Solution : The differential equation of the curve is: 
 Question 16. For the differential equation
Question 16. For the differential equation 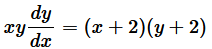 find the solution curve passing through the point (1,-1) Solution :
find the solution curve passing through the point (1,-1) Solution :  Question 17. Find the equation of the curve passing through the point (0,-2) given that at any point (x,y) on the curve the product of the slope of its tangent and y-coordinate of the point is equal to the x-coordinate of the point. Solution : Let x and y be the x -coordinate and y -coordinate of the curve respectively. We know that the slope of a tangent to the curve in the coordinate axis is given by the relation, dy/dx According to the given information, we get:
Question 17. Find the equation of the curve passing through the point (0,-2) given that at any point (x,y) on the curve the product of the slope of its tangent and y-coordinate of the point is equal to the x-coordinate of the point. Solution : Let x and y be the x -coordinate and y -coordinate of the curve respectively. We know that the slope of a tangent to the curve in the coordinate axis is given by the relation, dy/dx According to the given information, we get:  Now, the curve passes through point (0, –2). ∴ (–2) 2 – 0 2 = 2C ⇒ 2C = 4 Substituting 2C = 4 in equation (1), we get: y 2 – x 2 = 4 This is the required equation of the curve. Question 18. At any point ( x , y ) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (–4, –3). Find the equation of the curve given that it passes through (–2, 1). Solution : It is given that ( x , y ) is the point of contact of the curve and its tangent. The slope ( m 1 ) of the line segment joining ( x , y ) and (–4, –3) is y+3/x+4. We know that the slope of the tangent to the curve is given by the relation, dy/dx
Now, the curve passes through point (0, –2). ∴ (–2) 2 – 0 2 = 2C ⇒ 2C = 4 Substituting 2C = 4 in equation (1), we get: y 2 – x 2 = 4 This is the required equation of the curve. Question 18. At any point ( x , y ) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (–4, –3). Find the equation of the curve given that it passes through (–2, 1). Solution : It is given that ( x , y ) is the point of contact of the curve and its tangent. The slope ( m 1 ) of the line segment joining ( x , y ) and (–4, –3) is y+3/x+4. We know that the slope of the tangent to the curve is given by the relation, dy/dx  Substituting C = 1 in equation (1), we get: y + 3 = ( x + 4) 2 This is the required equation of the curve. Question 19. The volume of the spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of balloon after t seconds. Solution : Let the rate of change of the volume of the balloon be k (where k is a constant).
Substituting C = 1 in equation (1), we get: y + 3 = ( x + 4) 2 This is the required equation of the curve. Question 19. The volume of the spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of balloon after t seconds. Solution : Let the rate of change of the volume of the balloon be k (where k is a constant).  ⇒ 4π × 3 3 = 3 ( k × 0 + C) ⇒ 108π = 3C ⇒ C = 36π At t = 3, r = 6: ⇒ 4π × 6 3 = 3 ( k × 3 + C) ⇒ 864π = 3 (3 k + 36π) ⇒ 3 k = –288π – 36π = 252π ⇒ k = 84π Substituting the values of k and C in equation (1), we get:
⇒ 4π × 3 3 = 3 ( k × 0 + C) ⇒ 108π = 3C ⇒ C = 36π At t = 3, r = 6: ⇒ 4π × 6 3 = 3 ( k × 3 + C) ⇒ 864π = 3 (3 k + 36π) ⇒ 3 k = –288π – 36π = 252π ⇒ k = 84π Substituting the values of k and C in equation (1), we get:  Thus, the radius of the balloon after t seconds is
Thus, the radius of the balloon after t seconds is  .
.
Question 20. In a bank, principal increases continuously at the rate of r % per year. Find the value of r if Rs 100 doubles itself in 10 years (log e 2 = 0.6931).
Solution : Let p , t, and r represent the principal, time, and rate of interest respectively. It is given that the principal increases continuously at the rate of r % per year. Hence, the value of r is 6.93%.
Hence, the value of r is 6.93%.
Question 21. In a bank, principal increases continuously at the rate of 5% per year. An amount of Rs 1000 is deposited with this bank, how much will it worth after 10 years
(e 0.5 = 1.645).
Solution : Let p and t be the principal and time respectively. It is given that the principal increases continuously at the rate of 5% per year. Hence, after 10 years the amount will be worth Rs 1648. Question 22. In a culture the bacteria count is 1,00,000. The number is increased by 10% in 2 hours. In how many hours will the count reach 2,00,000, if the rate of growth of bacteria is proportional to the number present. Solution : Let y be the number of bacteria at any instant t . It is given that the rate of growth of the bacteria is proportional to the number present.
Hence, after 10 years the amount will be worth Rs 1648. Question 22. In a culture the bacteria count is 1,00,000. The number is increased by 10% in 2 hours. In how many hours will the count reach 2,00,000, if the rate of growth of bacteria is proportional to the number present. Solution : Let y be the number of bacteria at any instant t . It is given that the rate of growth of the bacteria is proportional to the number present. 
 Question 23. The general solution of the differential equation
Question 23. The general solution of the differential equation 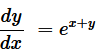 is:
is:  Solution :
Solution :  Therefore, option (A) is correct.
Therefore, option (A) is correct.NCERT Solutions For Class 12 Maths Chapter 9 Exercise 9.4 FAQs
Is differential equations easy class 12?
CBSE 12th maths introduces many advanced topics that can trouble students like differential equations. A great way to prepare for maths is by making mind maps. You can create them during the study and then use them for revision.
How many exercise are there in differential equations?
There are a total of 113 questions in the NCERT Solutions Class 12 Maths Chapter 9 Differential Equations that are divided among 7 exercises.
What is the main formula of a differential equation?
A differential equation contains derivatives which are either partial derivatives or ordinary derivatives. The derivative represents a rate of change, and the differential equation describes a relationship between the quantity that is continuously varying with respect to the change in another quantity.
Who uses differential equations?
There are various other applications of differential equations in the field of engineering (determining the equation of a falling object, Newton's Law of Cooling, the RL circuit equations, etc), physics, chemistry, geology, economics, etc.
Who invented calculus?
Calculus was primarily introduced by two scientists: Issac Newton and Gottfried Wilhelm Leibniz.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App









