
NCERT Solutions for Class 10 Maths Chapter 10 Exercise 10.2: NCERT Solutions for Class 10 Maths Chapter 10 Exercise 10.2 provide detailed and step-by-step explanations to help students understand the concepts of circles and their tangents.
This exercise focuses on solving problems related to the lengths of tangents drawn from an external point to a circle, a crucial topic for board exams. The solutions simplify complex concepts and offer accurate methods to solve questions, ensuring a solid foundation for better performance. These solutions are ideal for revising the chapter, strengthening problem-solving skills, and building confidence for exams.CBSE Class 10 Previous Year Question Papers
NCERT Solutions for Class 10 Maths Chapter 10 Exercise 10.2 Overview
This exercise in Chapter 10 Circles, primarily focuses on the geometrical properties and theorems related to tangents drawn from an external point to a circle. The key concept is that the lengths of tangents drawn from an external point to a circle are equal. The problems involve applying this theorem to solve practical and theoretical questions.CBSE Class 10 Maths Sample Paper 2024-25
Students are required to use given measurements and deduce unknown parameters using logical reasoning and mathematical formulas. The questions may also require constructing diagrams to aid in visualization and applying the Pythagoras theorem in some cases. This exercise strengthens students' understanding of tangents and circles while building problem-solving skills, making it an important part of the curriculum.Class 10 Maths Chapter 10 Exercise 10.2 Questions and Answers PDF
This PDF has clear solutions for all the questions in Exercise 10.2 of Class 10 Maths Chapter 10, Circles. It explains each answer step by step, making it easy to understand. The questions focus on tangents to a circle and related theorems. This PDF is a helpful resource for practicing, revising, and preparing for exams.Class 10 Maths Chapter 10 Exercise 10.2 Questions and Answers PDF
NCERT Solutions for Class 10 Maths Chapter 10 Exercise 10.2 FAQs
How are these solutions helpful for exams?
The solutions simplify complex problems, strengthen conceptual understanding, and cover exam-relevant questions, making them an essential resource for board exam preparation.
Do these solutions include diagrams?
Yes, the solutions include accurate diagrams to help students visualize problems and apply theorems correctly.
Can these solutions help with competitive exams?
Yes. The solutions build a strong foundation in geometry, which is helpful for various competitive exams.
Are the solutions easy to understand?
Yes, the solutions are written in simple and clear language with detailed steps, ensuring that students of all levels can follow and learn effectively.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App
 Let O be the centre of the circle.
Given that,
OQ = 25cm and PQ = 24 cm
As the radius is perpendicular to the tangent at the point of contact,
Therefore, OP ⊥ PQ
Applying Pythagoras theorem in ΔOPQ, we obtain
In right triangle OPQ,
[By Pythagoras theorem]
Let O be the centre of the circle.
Given that,
OQ = 25cm and PQ = 24 cm
As the radius is perpendicular to the tangent at the point of contact,
Therefore, OP ⊥ PQ
Applying Pythagoras theorem in ΔOPQ, we obtain
In right triangle OPQ,
[By Pythagoras theorem]
 OP = 7 cm
Therefore, the radius of the circle is 7 cm.
Hence, alternative 7 cm is correct.
2. In Fig. 10.11, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(A) 60°
(B) 70°
(C) 80°
(D) 90°
OP = 7 cm
Therefore, the radius of the circle is 7 cm.
Hence, alternative 7 cm is correct.
2. In Fig. 10.11, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(A) 60°
(B) 70°
(C) 80°
(D) 90°

 Therefore, the radius drawn to these tangents will be perpendicular to the tangents.
Thus, OA ⊥ PA and OB ⊥ PB
∠OBP = 90º
∠OAP = 90º
In AOBP,
Sum of all interior angles = 360°
∠OAP + ∠APB +∠PBO + ∠BOA = 360°
90° + 80° +90º +∠BOA = 360°
∠BOA = 100°
In ΔOPB and ΔOPA,
AP = BP (Tangents from a point)
OA = OB (Radii of the circle)
OP = OP (Common side)
Therefore, ΔOPB ≅ ΔOPA (SSS congruence criterion)
A ↔ B, P ↔ P, O ↔ O
And thus, ∠POB = ∠POA
Therefore, the radius drawn to these tangents will be perpendicular to the tangents.
Thus, OA ⊥ PA and OB ⊥ PB
∠OBP = 90º
∠OAP = 90º
In AOBP,
Sum of all interior angles = 360°
∠OAP + ∠APB +∠PBO + ∠BOA = 360°
90° + 80° +90º +∠BOA = 360°
∠BOA = 100°
In ΔOPB and ΔOPA,
AP = BP (Tangents from a point)
OA = OB (Radii of the circle)
OP = OP (Common side)
Therefore, ΔOPB ≅ ΔOPA (SSS congruence criterion)
A ↔ B, P ↔ P, O ↔ O
And thus, ∠POB = ∠POA
 Hence, alternative 50° is correct.
4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Hence, alternative 50° is correct.
4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
 To prove: CD || EF.
Proof: CD is the tangent to the circle at the point A.
∴ ∠BAD = 90°
EF is the tangent to the circle at the point B.
∴ ∠ABE = 90°
Thus, ∠BAD = ∠ABE (each equal to 90°).
But these are alternate interior angles.
∴ CD || EF
5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
To prove: CD || EF.
Proof: CD is the tangent to the circle at the point A.
∴ ∠BAD = 90°
EF is the tangent to the circle at the point B.
∴ ∠ABE = 90°
Thus, ∠BAD = ∠ABE (each equal to 90°).
But these are alternate interior angles.
∴ CD || EF
5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
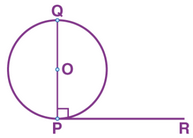 Let, O is the centre of the given circle.
A tangent PR has been drawn touching the circle at point P.
Draw QP ⊥ RP at point P, such that point Q lies on the circle.
∠OPR = 90° (radius ⊥ tangent)
Also, ∠QPR = 90° (Given)
∴ ∠OPR = ∠QPR
Now, the above case is possible only when centre O lies on the line QP.
Hence, perpendicular at the point of contact to the tangent to a circle passes through the centre of the circle.
6. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Let, O is the centre of the given circle.
A tangent PR has been drawn touching the circle at point P.
Draw QP ⊥ RP at point P, such that point Q lies on the circle.
∠OPR = 90° (radius ⊥ tangent)
Also, ∠QPR = 90° (Given)
∴ ∠OPR = ∠QPR
Now, the above case is possible only when centre O lies on the line QP.
Hence, perpendicular at the point of contact to the tangent to a circle passes through the centre of the circle.
6. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
 In right ΔOPQ, we have
OQ
2
=OP
2
+PQ
2
[Using Pythagoras Theorem]
OP
2
= (5)
2
– (4)
2
= 25 – 16 =9
⇒ OP = 3 cm
Hence, the radius of the circle is 3 cm.
7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In right ΔOPQ, we have
OQ
2
=OP
2
+PQ
2
[Using Pythagoras Theorem]
OP
2
= (5)
2
– (4)
2
= 25 – 16 =9
⇒ OP = 3 cm
Hence, the radius of the circle is 3 cm.
7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
 In Δ OAC,
In Δ OAC,
 ⇒ AC = 4cm
∴ AB = 2AC (Since perpendicular drawn from the center of the circle bisects the chord)
∴ AB = 2 × 4 = 8cm
The length of the chord of the larger circle is 8 cm.
8. A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that:
AB + CD = AD + BC
⇒ AC = 4cm
∴ AB = 2AC (Since perpendicular drawn from the center of the circle bisects the chord)
∴ AB = 2 × 4 = 8cm
The length of the chord of the larger circle is 8 cm.
8. A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that:
AB + CD = AD + BC


 Let us Consider a circle with centre O. Let P be an external point from which two tangents PA and PB are drawn to the circle which are touching the circle at point A and B respectively and AB is the line segment, joining point of contacts A and B together such that it subtends ∠AOB at center O of the circle.
It can be observed that
OA ⊥ PA
∴ ∠OAP = 90°
Similarly, OB ⊥ PB
∴ ∠OBP = 90°
In quadrilateral OAPB,
Sum of all interior angles = 360º
∠OAP +∠APB +∠PBO +∠BOA = 360º
⇒ 90º + ∠APB + 90º + ∠BOA = 360º
⇒ ∠APB + ∠BOA = 180º
∴ The angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
11. Prove that the parallelogram circumscribing a circle is a rhombus.
Let us Consider a circle with centre O. Let P be an external point from which two tangents PA and PB are drawn to the circle which are touching the circle at point A and B respectively and AB is the line segment, joining point of contacts A and B together such that it subtends ∠AOB at center O of the circle.
It can be observed that
OA ⊥ PA
∴ ∠OAP = 90°
Similarly, OB ⊥ PB
∴ ∠OBP = 90°
In quadrilateral OAPB,
Sum of all interior angles = 360º
∠OAP +∠APB +∠PBO +∠BOA = 360º
⇒ 90º + ∠APB + 90º + ∠BOA = 360º
⇒ ∠APB + ∠BOA = 180º
∴ The angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
11. Prove that the parallelogram circumscribing a circle is a rhombus.
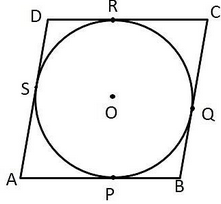 Given: ABCD is a parallelogram circumscribing a circle.
To Prove: ABCD is a rhombus.
Proof: Since, the tangents from an external point to a circle are equal.
We know that the tangents drawn to a circle from an exterior point are equal in length.
∴ AP = AS, BP = BQ, CR = CQ and DR = DS.
AP + BP + CR + DR = AS + BQ + CQ + DS
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
∴ AB + CD = AD + BC or 2AB = 2BC (since AB = DC and AD = BC)
∴ AB = BC = DC = AD.
Therefore, ABCD is a rhombus.
Hence, proved.
12. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC.
Given: ABCD is a parallelogram circumscribing a circle.
To Prove: ABCD is a rhombus.
Proof: Since, the tangents from an external point to a circle are equal.
We know that the tangents drawn to a circle from an exterior point are equal in length.
∴ AP = AS, BP = BQ, CR = CQ and DR = DS.
AP + BP + CR + DR = AS + BQ + CQ + DS
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
∴ AB + CD = AD + BC or 2AB = 2BC (since AB = DC and AD = BC)
∴ AB = BC = DC = AD.
Therefore, ABCD is a rhombus.
Hence, proved.
12. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC.


 13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
 Let ABCD be a quadrilateral circumscribing a circle with O such that it touches the circle at point P, Q, R, S. Join the vertices of the quadrilateral ABCD to the center of the circle.
In ΔOAP and ΔOAS,
AP = AS (Tangents from the same point)
OP = OS (Radii of the circle)
OA = OA (Common side)
ΔOAP ≅ ΔOAS (SSS congruence condition)
∴ ∠POA = ∠AOS
⇒∠1 = ∠8
Similarly we get,
∠2 = ∠3
∠4 = ∠5
∠6 = ∠7
Adding all these angles,
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 +∠8 = 360º
⇒ (∠1 + ∠8) + (∠2 + ∠3) + (∠4 + ∠5) + (∠6 + ∠7) = 360º
⇒ 2 ∠1 + 2 ∠2 + 2 ∠5 + 2 ∠6 = 360º
⇒ 2(∠1 + ∠2) + 2(∠5 + ∠6) = 360º
⇒ (∠1 + ∠2) + (∠5 + ∠6) = 180º
⇒ ∠AOB + ∠COD = 180º
Similarly, we can prove that ∠ BOC + ∠ DOA = 180º
Hence, opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Let ABCD be a quadrilateral circumscribing a circle with O such that it touches the circle at point P, Q, R, S. Join the vertices of the quadrilateral ABCD to the center of the circle.
In ΔOAP and ΔOAS,
AP = AS (Tangents from the same point)
OP = OS (Radii of the circle)
OA = OA (Common side)
ΔOAP ≅ ΔOAS (SSS congruence condition)
∴ ∠POA = ∠AOS
⇒∠1 = ∠8
Similarly we get,
∠2 = ∠3
∠4 = ∠5
∠6 = ∠7
Adding all these angles,
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 +∠8 = 360º
⇒ (∠1 + ∠8) + (∠2 + ∠3) + (∠4 + ∠5) + (∠6 + ∠7) = 360º
⇒ 2 ∠1 + 2 ∠2 + 2 ∠5 + 2 ∠6 = 360º
⇒ 2(∠1 + ∠2) + 2(∠5 + ∠6) = 360º
⇒ (∠1 + ∠2) + (∠5 + ∠6) = 180º
⇒ ∠AOB + ∠COD = 180º
Similarly, we can prove that ∠ BOC + ∠ DOA = 180º
Hence, opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.









