NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.1
Get detailed NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.1. Understand coordinate geometry concepts like distance formula and midpoint formula with step-by-step explanations and solutions to practice problems. Perfect for exam preparation and building a strong foundation in coordinate geometry.
Ananya Gupta7 Jan, 2025
Share
NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.1: NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Exercise 7.1 focus on understanding the Cartesian plane and plotting points on it. This exercise involves solving problems related to the distance formula, midpoint formula, and basic understanding of coordinates.
Students are expected to find the distance between two points, determine the midpoint of a line segment, and use the Pythagorean theorem in the coordinate plane. The solutions provide detailed step-by-step explanations, helping students grasp the concepts with ease and practice problem-solving techniques effectively. These solutions are created to reinforce the understanding of coordinate geometry principles.CBSE Class 12th Topper Answer Sheet
NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.1 Overview
NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.1 focuses on the foundational concepts of coordinate geometry. In this exercise, students learn about plotting points on the Cartesian plane, understanding the distance between two points, and finding the midpoint of a line segment.CBSE Class 12 Previous Year Question Papers
Here’s an overview of the key concepts covered in Exercise 7.1:- Plotting Points on the Cartesian Plane : Students are introduced to the Cartesian coordinate system, where points are represented by their coordinates (x, y). This concept helps in visualizing the relationship between numbers and their corresponding points on the plane.
- Distance Formula : The exercise explains how to calculate the distance between two points using the distance formula, which is derived from the Pythagorean theorem.
- Midpoint Formula : Students learn how to find the midpoint of a line segment given its endpoints. The midpoint formula is used to determine the point that divides the line segment into two equal parts.
NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.1 PDF
The NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.1 provide a detailed and step-by-step explanation of important coordinate geometry concepts such as plotting points on the Cartesian plane, calculating the distance between two points, and finding the midpoint of a line segment. You can easily download the PDF of NCERT Solutions for Exercise 7.1 using the link available below, ensuring you have quick access to detailed solutions for better learning.NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.1 PDF
NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1
Solve the followings Questions.
1. Find the distance between the following pairs of points: (i) (2, 3), (4,1) (ii) (–5, 7), (–1, 3) (iii) (a, b), (–a, –b)Answer:
(i) Distance between the points is given by
Therefore the distance between (2,3) and (4,1) is given by
l =
=
.png)
= √4+4 = √8 = 2√2
(ii)Applying Distance Formula to find distance between points (–5, 7) and (–1, 3), we get
l =
=
= √16+16 = √32 = 4√2
(iii)Applying Distance Formula to find distance between points (a, b) and (–a, –b), we get
l =
=
=
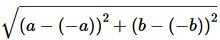2. Find the distance between the points (0, 0) and (36, 15). Also, find the distance between towns A and B if town B is located at 36 km east and15 km north of town A.
Answer:
Applying Distance Formula to find distance between points (0, 0) and (36, 15), we get =
= √1296 + 225 = √1521 = 39
Yes, we can find the distance between the given towns A and B.
Assume town A at origin point (0, 0).
Therefore, town B will be at point (36, 15) with respect to town A.
And hence, as calculated above, the distance between town A and B will be 39km.
3. Determine if the points (1, 5), (2, 3) and (–2, –11) are collinear.
Answer:
Let A = (1, 5), B = (2, 3) and C = (–2, –11) Using Distance Formula to find distance AB, BC and CA.
BC =
CA =
Since AB+BC ≠ CA
Therefore, the points (1, 5), (2, 3), and (−2, −11) are not collinear.
4. Check whether (5, –2), (6, 4) and (7, –2) are the vertices of an isosceles triangle.
Answer:
Let A = (5, –2), B = (6, 4) and C = (7, –2) Using Distance Formula to find distances AB, BC and CA. AB =
BC =
CA =
Since AB = BC.
Therefore, A, B and C are vertices of an isosceles triangle.
5. In a classroom, 4 friends are seated at the points A (3, 4), B (6, 7), C (9, 4) and D (6, 1). Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli. “Don’t you think ABCD is a square?”Chameli disagrees. Using distance formula, find which of them is correct.
Answer:
We have A = (3, 4), B = (6, 7), C = (9, 4) and D = (6, 1) Using Distance Formula to find distances AB, BC, CD and DA, we get AB =
BC =
CD =
AD =
Therefore, All the sides of ABCD are equal here
Now, we will check the length of its diagonals.
AC =
BD =
So, Diagonals of ABCD are also equal.
we can definitely say that ABCD is a square.
Therefore, Champa is correct.
6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
(i) (–1, –2), (1, 0), (–1, 2), (–3, 0)
(ii) (–3, 5), (3, 1), (0, 3), (–1, –4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Answer:
(i)Let A = (–1, –2), B = (1, 0), C= (–1, 2) and D = (–3, 0) Using Distance Formula to find distances AB, BC, CD and DA, we get AB =
BC =
CD =
AD =
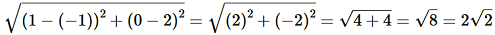
.png)
Therefore, all four sides of quadrilateral are equal.
Now, we will check the length of diagonals.
AC =
.png)
BD =
Therefore, diagonals of quadrilateral ABCD are also equal.
we can say that ABCD is a square.
(ii)Let A = (–3, 5), B= (3, 1), C= (0, 3) and D= (–1, –4)
Using Distance Formula to find distances AB, BC, CD and DA, we get
AB =
BC =
CD =
DA =
We cannot find any relation between the lengths of different sides.
Therefore, we cannot give any name to the quadrilateral ABCD.
(iii)Let A = (4, 5), B= (7, 6), C= (4, 3) and D= (1, 2)
Using Distance Formula to find distances AB, BC, CD and DA, we get
AB =
BC =
CD =
DA =
Here opposite sides of quadrilateral ABCD are equal.
We can now find out the lengths of diagonals.
AC =
BD =
Here diagonals of ABCD are not equal.
we can say that ABCD is not a rectangle therefore it is a parallelogram.
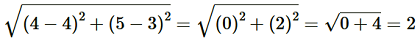
7. Find the point on the x–axis which is equidistant from (2, –5) and (–2, 9).
Answer:
Let the point be (x, 0) on x–axis which is equidistant from (2, –5) and (–2, 9). Using Distance Formula and according to given conditions we have:
⇒
Squaring both sides, we get
⇒
(x-2)² + 25 = (x+2)² + 81
x² + 4 - 4x + 25 = x² + 4 + 4x + 81
8x = - 25 - 81
8x = -56
x = - 7
Therefore, point on the x–axis which is equidistant from (2, –5) and (–2, 9) is (–7, 0)
8. Find the values of y for which the distance between the points P (2, –3) and Q (10, y) is 10 units.
Answer:
Using Distance formula, we have
⇒
⇒ 64 + (y +3)² = 100
⇒ (y+3)² = 100-64 = 36
⇒ y+3 = ± 6
⇒ y+3=6 or y+3 = - 6
Therefore y = 3 or -9
9. If, Q (0, 1) is equidistant from P (5, –3) and R (x, 6), find the values of x. Also, find the distances QR and PR.
Answer:
It is given that Q is equidistant from P and R. Using Distance Formula, we get PQ = RQ
⇒√25+16 = √x² + 25
⇒41 = x² + 25
16 = x²
x = ± 4
Thus, R is (4, 6) or (–4, 6).
When point R is (4,6)
PR =
QR =
When point R is (- 4,6)
PR =
QR =
10. Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (–3, 4).
Answer:
It is given that (x, y) is equidistant from (3, 6) and (–3, 4). Using Distance formula, we can write
⇒
⇒ (x-3)² + (y-6)² = (x+3)² + (y-4)²
⇒ x² + 9 -6x + y² + 36 - 12y = x² + 9 + 6x + y² + 16 - 8y
⇒36- 16 = 6x + 6x + 12y - 8y
⇒20 = 12x + 4y
⇒3x + y = 5
⇒3x + y - 5 = 0
Benefits of Solving NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1
NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.1 FAQs
What is covered in Exercise 7.1 of Coordinate Geometry?
Exercise 7.1 focuses on the basics of coordinate geometry, including plotting points on a coordinate plane, understanding the distance formula, and applying the midpoint formula.
Can I apply the distance formula to points on a straight line?
Yes, the distance formula can be used to find the distance between two points on a straight line, curved line, or any two points on the coordinate plane.
What is the importance of the midpoint formula in coordinate geometry?
The midpoint formula is crucial for finding the center point between two given points, which is often needed in problems related to geometry, symmetry, and constructing shapes.
Are there any tricky questions in this exercise?
The exercise is primarily focused on the application of the distance and midpoint formulas, but some problems may involve multi-step solutions or require careful attention to coordinate signs (positive or negative). However, with practice, these problems become easier to tackle.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.