Introduction to Trigonometry Class 10 Maths Chapter 8 Exercise 8.3 PDF

 NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.3: Introduction to Trigonometry Class 10 Exercise 8.3: NCERT Class 10 Maths Chapter 8 Exercise 8.3 focuses on trigonometric identities, especially the fundamental identity sin2θ+cos2θ=1, and its related forms. The exercise includes proof-based questions and simplification problems that are commonly asked in CBSE board exams.

This part of Chapter 8 is important for scoring marks in short and long-answer questions, as it helps students improve accuracy while solving identities involving sin, cos, and tan. Learning these concepts prepares learners for better performance in Class 10 board exams. 

• Angle of Elevation: The angle formed when an observer looks upward at an object.
• Angle of Depression: The angle formed when an observer looks downward at an object.

Class 10 Maths Introduction to Trigonometry Exercise 8.3 Solutions 

Below are the NCERT Solutions for Class 10 Maths Chapter 8 – Introduction to Trigonometry Exercise 8.3. Students should also practise these questions, as they help revise important identities, improve accuracy, and build confidence for exams.

Solve the following Questions.

1. Evaluate the following : 
(i) sin 60° cos 30° + sin 30° cos 60°

(ii) 2 tan ² 45° + cos ² 30° – sin ² 60°

(iii) cos 45°/(sec 30° + cosec 30°)

(iv) (sin 30° + tan 45° – cosec 60°)/(sec 30° + cos 60° + cot 45°)

(v) (5cos ² 60° + 4sec ² 30° - tan ² 45°)/(sin ² 30° + cos ² 30°)

Answer:

(i) sin 60° cos 30° + sin 30° cos 60

°

(ii) 2 tan ² 45° + cos ² 30° – sin ² 60°

(iii) cos 45°/(sec 30° + cosec 30°)

iv) (sin 30° + tan 45° – cosec 60°)/(sec 30° + cos 60° + cot 45°)

(v) (5cos ² 60° + 4sec ² 30° - tan ² 45°)/(sin ² 30° + cos ² 30°

)

2. Choose the correct option and justify your choice :
(i) 2tan 30°/1+tan ² 30° = (A) sin 60°   (B) cos 60°  (C) tan 60°  (D) sin 30°

(ii) 1-tan ² 45°/1+tan ² 45° = (A) tan 90°   (B) 1        (C) sin 45°      (D) 0

(iii)  sin ² A = 2 sin A is true when A = (A) 0°        (B) 30°      (C) 45°              (D) 60°

(iv) 2tan30°/1-tan ² 30° = (A) cos 60°   (B) sin 60°  (C) tan 60°  (D) sin 30°

Answer:

(i) 2tan 30°/1+tan ² 30° = (A) sin 60°   (B) cos 60°  (C) tan 60°  (D) sin 30° 

(ii) 1-tan ² 45°/1+tan ² 45° = (A) tan 90°   (B) 1        (C) sin 45°      (D) 0

(iii) sin ² A = 2 sin A is true when A = (A) 0°        (B) 30°      (C) 45°              (D) 60°

(iv) 2tan30°/1-tan ² 30° = (A) cos 60°   (B) sin 60°  (C) tan 60°  (D) sin 30°

3. If tan (A + B) = √3 and tan (A – B) = 1/√3; 0° < A + B ≤ 90°; A > B, find A and B.

Answer:

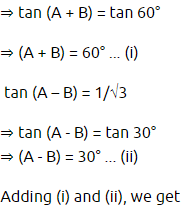
4. State whether the following are true or false. Justify your answer. 

(i) sin (A + B) = sin A + sin B.

(ii) The value of sin θ increases as θ increases.

(iii) The value of cos θ increases as θ increases.

(iv) sin θ = cos θ for all values of θ. (v) cot A is not defined for A = 0°.

Answer:

(i) False. Let A = 30° and B = 60°, then sin (A + B) = sin (30° + 60°) = sin 90° = 1 and, sin A + sin B = sin 30° + sin 60° = 1/2 + √3/2 = 1+√3/2

(ii) True. sin 0° = 0 sin 30° = 1/2 sin 45° = 1/√2 sin 60° = √3/2 sin  90° = 1 Thus the value of sin θ increases as θ increases.

(iii) False. cos 0° = 1 cos 30° = √3/2 cos 45° = 1/√2 cos 60° = 1/2 cos 90° = 0 Thus the value of cos θ decreases as θ increases.

(iv) True. cot A = cos A/sin A cot 0° = cos 0°/sin 0° = 1/0 = undefined.ion.

Class 10 Introduction to Trigonometry Exercise 8.3 PDF

The Class 10 Introduction to Trigonometry Exercise 8.3 PDF provides clear, step-by-step solutions aligned with the CBSE Class 10 Maths syllabus.

It focuses on important trigonometric identities and identity-based proofs that help students improve their reasoning and calculation accuracy. This PDF is perfect for revision, building confidence, and strengthening problem-solving skills for board exam preparation.

Introduction to Trigonometry Class 10 Exercise 8.3 PDF