
Oscillatory Motion Formula: Oscillatory motion involves an object repeatedly moving back and forth over a specific area. The most ideal conditions for this motion can be achieved in a complete vacuum where the absence of air prevents friction from impeding the object's oscillatory movement.
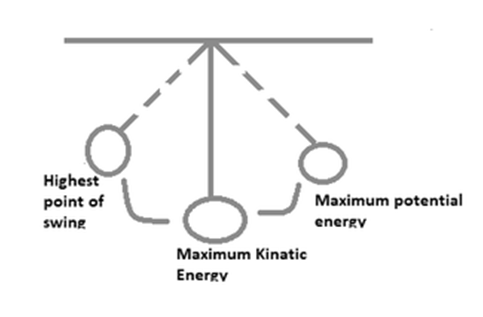
Consider the illustration of a pendulum below.
Oscillatory Motion Formula
Vibrations in strings and the motion of a spring represent oscillatory movements within the mechanical realm and are synonymous with mechanical vibrations. It's important not to mistake periodic motion for oscillatory motion. Objects engaged in periodic motion replicate their movement after specific intervals of time, whereas those in oscillatory motion repeat their movement within a particular position.
Hooke’s Law is fundamental in understanding Basic Harmonic Motion (SHM), a simple form of oscillatory motion. In this type of motion, the restoring force is directly proportional to the displacement from the equilibrium position, a principle known as Hooke’s Law.
Let's consider a scenario where a block of mass 'm' is attached to one end of a long spring (with a spring constant 'k'), while the other end is fixed to a wall. Hooke’s law defines the restoring force acting to rectify the spring's deformation.
Oscillatory Motion Formula : T=2π √ l / g
Where: l represents the length of the pendulum g denotes the acceleration due to gravity
Oscillatory Motion Formula Solved Examples
Example 1: Assuming 'g' remains constant, when does a simple pendulum double its period?
Solution: The Oscillatory Motion Formula for the period of a pendulum is T=2π √ l / g
If the length of the pendulum is increased to four times its original length:
T ′ =2π √ 4l / g
=2[2π √ l / g ]
=2T
Therefore, to double the period, the length must be increased to four times its original value, given that 'g' remains constant.
Example 2: If the length of a simple pendulum is reduced by one-fourth, what happens to its period? Assuming 'g' remains constant.
Solution: The Oscillatory Motion Formula of a simple pendulum is given by T=2π √ l / g .
If the length of the pendulum is decreased to one-fourth of its original length:
T ′ =2π √ l/4 / g =2π √ l /4 g =π √ l / g = T/2
Therefore, if the length of the pendulum is reduced to one-fourth of its original value while 'g' remains constant, the period is halved.
Example 3: Calculate the length of a pendulum with a period of 0.7 seconds.
Solution: The Oscillatory Motion Formula for the period of a pendulum in terms of its length l is given by 2π √ l / g .
Manipulating the formula to solve for
T 2 =4π 2 × l/g =
l= T 2/ 4π 2 ×g
= (0.7) 2/ 4π 2 ×9.8
This results in l=0.121 meters.
Example 4: If the length of a pendulum is increased to four times its original length, how does this change affect its period?
Solution: Given the Oscillatory Motion Formula T=2π √ l / g
If the length is increased to four times its original length, denoted as 4
T ′ =2π √ 4l / g
=2π×2 √ l / g
=2×(2π √ l / g )
=2T Therefore, if the length is increased to four times its original value, the period will become 2 times the initial period.
Oscillatory motion involves the repetitive back-and-forth movement of objects within a defined space. Ideal conditions for this motion are found in a vacuum, devoid of air to prevent friction from hindering the object's oscillations. Mechanical vibrations in strings and spring motions represent forms of oscillatory movement within the mechanical field. It's essential to differentiate between periodic and oscillatory motion: periodic motion involves replicating movement after specific time intervals, while oscillatory motion repeats movement within a specific position.
Hooke’s Law, which states that the restoring force is proportional to displacement from the equilibrium position, is fundamental in understanding Simple Harmonic Motion (SHM), a basic form of oscillatory motion. The period of a pendulum is given by the formula T=2π √ l / g, where 'l' represents the length of the pendulum and 'g' symbolizes the acceleration due to gravity.
| Related Links | |
| Thermal Expansion Formula | Hookes Law Formula |
| Spring Force Formula | Doppler Shift Formula |
Oscillatory Motion Formula FAQs
What is oscillatory motion?
What conditions are ideal for oscillatory motion?
What is the significance of Hooke’s Law in oscillatory motion?
How is the period of a pendulum calculated?










