Polarization Formula, Definition, Solved Examples

Definition of Polarization

Polarization Formula: Polarization refers to the orientation of oscillations in a transverse wave, such as light. It involves the direction in which the electromagnetic fields associated with the wave vibrate. Understanding polarization is essential as it allows us to control and manipulate light properties. Whether you're working with polarized sunglasses, optical devices, or satellite communications, a grasp of polarization is fundamental.

Polarization Formulas

Polarization Formula: Polarization is mathematically represented through various formulas, which quantify different aspects of polarized light. Here are some of the key polarization formulas:

1. Degree of Polarization (DoP) Formula:

The Degree of Polarization (DoP) is a measure of how polarized light is. It ranges from 0 (completely unpolarized) to 1 (fully polarized). The DoP formula is calculated as:

DoP = (Imax - Imin) / (Imax + Imin)

In this formula, Imax represents the maximum intensity, and Imin is the minimum intensity of the polarized light.

2. Polarization Angle Formula:

The polarization angle, often denoted as θ, indicates the angle at which the electric field vector oscillates concerning a reference axis. It can be calculated using trigonometric functions, depending on the wave's orientation. The formula is:

θ = tan ^-1 (Ey / Ex)

Here, Ex and Ey are the components of the electric field vector in the x and y directions, respectively.

3. Stokes Parameters:

The Stokes parameters are a set of four parameters that fully describe the polarization state of light. They offer a comprehensive representation of polarized light and are calculated using a series of measurements and mathematical operations.

Malus's Law

Polarization Formula: Malus's Law, named after Étienne-Louis Malus, is a fundamental principle in optics that explains how the intensity of polarized light changes as it passes through a polarizer. This law helps us understand how polarizers affect light.

Mathematically, Malus's Law is represented as:

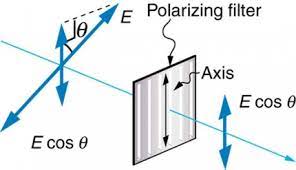
I = I ₀ * cos²(θ)

Where:

• I represents the intensity of the light after it passes through the polarizer.

• I ₀ is the initial intensity of unpolarized light.

• θ is the angle between the direction of the incident unpolarized light and the axis of the polarizer.

Key points about Malus's Law:

1. It quantifies how much of the incident light's intensity is transmitted through a polarizer.
2. When the incident light is perfectly aligned with the polarizer (θ = 0°), all of its intensity is transmitted (I = I0).
3. When the incident light is perpendicular to the polarizer (θ = 90°), none of its intensity is transmitted (I = 0).
4. As the angle θ varies between 0° and 90°, the transmitted intensity changes as the square of the cosine of the angle.

Also Check – Shear Modulus Formula

Brewster's Law

Polarization Formula: Brewster's Law, named after Sir David Brewster, is a principle that explains the angle of incidence at which reflected light becomes completely polarized when it hits a dielectric surface, such as glass or water.

Brewster's Law can be expressed as:

tan(θ _B ) = n ₂ / n ₁

Where:

• θB is Brewster's angle, the angle of incidence at which reflection is purely polarized.

• n1 is the refractive index of the first medium (usually air or vacuum).

• n2 is the refractive index of the second medium (the medium where the light is incident, like glass or water).

Key points about Brewster's Law:

1. Brewster's Law explains how polarized sunglasses work by reducing glare. When light reflects off a surface at Brewster's angle, it becomes partially or completely polarized.
2. At Brewster's angle, the reflected light is purely polarized in the plane parallel to the surface, which is valuable in anti-glare coatings on windows, camera lenses, and other applications.
3. The angle of polarization varies for different materials due to differences in refractive indices.

These laws are essential for understanding polarized light and how it can be controlled and utilized in various applications, including optics and communication systems.

Also Check – Tangential Velocity Formula

Solved Examples of Polarization Formula

Question 1: Calculate the degree of polarization (DoP) for light with maximum and minimum intensities of 500 and 100, respectively.

Solution:

DoP = (Imax - Imin) / (Imax + Imin)

DoP = (500 - 100) / (500 + 100)

DoP = 400 / 600

DoP = 2/3 or approximately 0.67

Question 2: Find the polarization angle (θ) when the electric field vector has components Ex = 3 and Ey = 4.

Solution:

θ = arctan(Ey / Ex)

θ = arctan(4 / 3)

θ ≈ 53.13 degrees

Question 3: A beam of light passes through a polarizer, and the transmitted intensity is reduced to half of the incident intensity. Calculate the degree of polarization.

Solution:

DoP = (Imax - Imin) / (Imax + Imin)

Since the transmitted intensity is half of the incident intensity, Imax = 1 and Imin = 0.5.

DoP = (1 - 0.5) / (1 + 0.5)

DoP = 0.5 / 1.5

DoP ≈ 1/3 or approximately 0.33

Also Check – Horsepower Formula

Question 4: Determine the Stokes parameters S0, S1, S2, and S3 for a beam of polarized light.

Solution:

The Stokes parameters can be determined through measurements and calculations based on the characteristics of the polarized light. They are not directly calculated from given values but are obtained experimentally.

Question 5: What is the significance of circular polarization in optical communication?

Solution:

Circular polarization in optical communication is significant because it allows for the transmission of information using two orthogonal circular polarization states. This reduces the impact of signal fading due to polarization changes, making it useful in free-space optical communication and satellite links.

Question 6: Explain how Brewster's angle is related to polarization.

Solution:

Brewster's angle is the angle of incidence at which reflected light becomes completely polarized. This angle is related to polarization because it results in only the parallel component of the incident light being transmitted, while the perpendicular component is absorbed. Hence, it's a critical concept in understanding polarization.

Question 7: How does polarized sunglasses work?

Solution:

Polarized sunglasses contain a polarizing filter that blocks light oscillating in certain directions. This reduces glare and improves visibility, especially when light is reflected off surfaces like water or roads. The filter allows only vertically polarized light to pass through, effectively reducing horizontal glare.

Question 8: Describe the Malus's law and its applications.

Solution:

Malus's law states that the intensity of light (I) passing through a polarizer is proportional to the square of the cosine of the angle (θ) between the polarizer and the incident light. Mathematically, it is expressed as I = I0 * cos²(θ). Malus's law finds applications in understanding how polarizers affect light intensity and in various optical devices like sunglasses, LCD screens, and photography.

Question 9: What is depolarization in the context of light propagation?

Solution:

Depolarization refers to the loss of the original polarization state of light. This can occur due to scattering or randomization of the wave's oscillation direction. Depolarized light contains a mixture of various polarization states and no longer exhibits a consistent polarization orientation.

Question 10: How is circular polarization different from linear polarization?

Solution:

Circular polarization involves an electric field vector that rotates as the wave propagates, creating a helical pattern. Linear polarization, on the other hand, has an electric field that oscillates in a single direction. Circular polarization is characterized by both amplitude and phase modulation, while linear polarization involves only amplitude modulation.

[wp-faq-schema title=" Polarization Formula FAQs" accordion=1