
Pythagorean Theorem Formula: The Pythagorean theorem asserts that in a right-angled triangle, the square of the hypotenuse equals the sum of the squares of the other two sides. Consider the triangle ABC, where BC 2 = AB 2 + AC 2 . In this context, AB represents the base, AC is the altitude (height), and BC is the hypotenuse. It's important to note that the hypotenuse is the longest side in a right-angled triangle.
Pythagorean Theorem Formula Equation
The Pythagorean theorem, represented by the equation c 2 = a 2 + b 2 , applies to right triangles, where 'c' is the length of the hypotenuse, and 'a' and 'b' are the lengths of the other two sides. Therefore, whenever you have a right triangle with a 90-degree angle, you can utilize the Pythagorean equation to relate the side lengths

History of Pythagoras Theorem
The Pythagorean theorem is commonly attributed to the Greek mathematician Pythagoras of Samos, who indeed made significant contributions to mathematics and formed a group of scholars. However, it's worth noting that there is evidence suggesting that the concept of this theorem existed in other civilizations, such as the Old Babylonians, as far back as the 20th to the 16th century B.C., long before Pythagoras' time. So, while Pythagoras is famous for it, the idea of the theorem predates him in various ancient cultures.
Pythagoras Theorem Formula
The Pythagorean theorem, as expressed in the formula c 2 = a 2 + b 2 for a right triangle ABC, signifies that the square of the hypotenuse (BC) equals the sum of the squares of the other two sides (AB and AC). This relationship can also be visualized by considering the areas of squares constructed on these sides. In a right-angled triangle, the Pythagorean theorem is represented as c 2 = a 2 + b 2 , where 'c' denotes the hypotenuse, and 'a' and 'b' denote the other two legs.
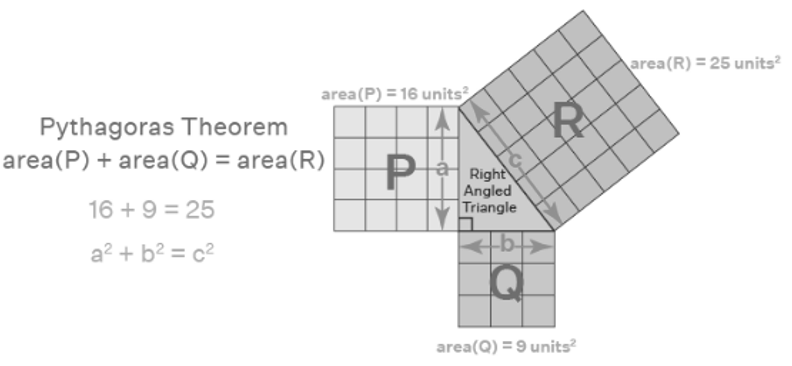
Pythagoras Theorem Proof
The Pythagorean theorem can be proven through various methods, with two common approaches being the algebraic method and the method involving similar triangles. Let's explore both methods individually to understand the theorem's proof.
Proof of the Pythagorean Theorem Using the Algebraic Method
Start with four congruent right-angled triangles, where 'a' and 'b' are the side lengths, and 'c' is the hypotenuse. Arrange them to create a tilted square, PQRS, with sides of length 'a + b'. The triangles have 'b' as the base, 'a' as the height, and 'c' as the hypotenuse.
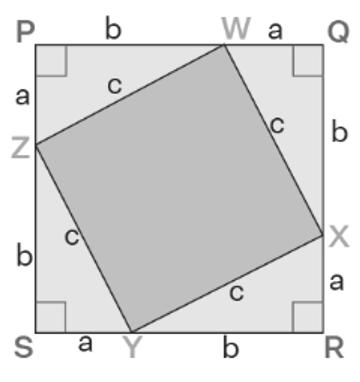
The four triangles form an inner square, WXYZ, with 'c' as the four sides.
The area of square WXYZ, formed by arranging the four triangles, is c 2 .
The area of square PQRS, with side length (a + b), is equal to the sum of the areas of the four triangles plus the area of square WXYZ. This leads to (a + b) 2 = [4 × 1/2 × (a × b)] + c 2 .
Simplifying further, you get a 2 + b 2 + 2ab = 2ab + c 2 . Therefore, a 2 + b 2 = c 2 , which proves the Pythagorean theorem formula.
In essence, this algebraic method demonstrates the validity of the Pythagorean theorem
Pythagorean Theorem Formula Using Similar Triangles
Similarity between two triangles is determined when their corresponding angles have equal measures, and their corresponding sides are in the same ratio. In essence, matching angles in similar triangles imply proportional side lengths, and this relationship can also be confirmed using the sine law, as equal angles result in the same ratios of side lengths
Derivation of Pythagorean Theorem Formula
The Pythagorean theorem using similar triangles:
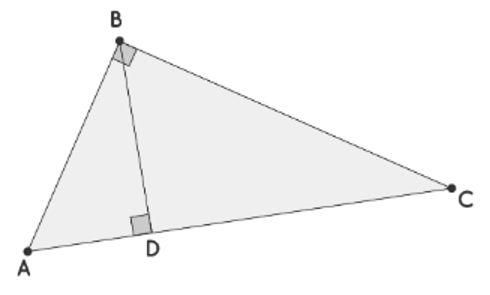
Consider a right-angled triangle ABC with the right angle at B. Draw a perpendicular BD, which intersects AC at point D.
In triangles ABD and ACB:
Angle A is common.
Angle ADB is equal to angle ABC (both are right angles).
Therefore, triangles ABD and ACB are similar due to the Angle-Angle (AA) similarity criterion.
Similarly, we can show that triangles BCD and ACB are also similar.
Hence, we have the similarity relationships: ABD ∼ ACB and BCD ∼ ACB.
From ABD ∼ ACB, we can write AD/AB = AB/AC, which leads to AD × AC = AB 2 .
Similarly, from BCD ∼ ACB, we can write CD/BC = BC/AC, which implies CD × AC = BC 2 .
Adding these two equations together, we obtain AB 2 + BC 2 = AC(AD + DC).
Substituting AD + DC with AC, we finally arrive at the Pythagorean theorem: AB 2 + BC 2 = AC 2 .
This demonstrates the proof of the Pythagorean theorem using similar triangles.
Pythagoras Theorem Triangles
Right triangles that adhere to the Pythagorean theorem are often referred to as Pythagorean theorem triangles. The three sides of such triangles, collectively known as Pythagorean triples, satisfy the theorem, which defines that the square of the hypotenuse is equal to the sum of the squares of the two legs. This relationship is expressed as c 2 = a 2 + b 2 , where 'c' defines the hypotenuse, and 'a' and 'b' define the two legs of the triangle.
Pythagoras Theorem Square
According to the Pythagorean theorem, the area of the square constructed on the hypotenuse of a right triangle is indeed equal to the combined area of the squares built on the other two sides of the triangle. These squares are commonly referred to as Pythagoras squares, illustrating the fundamental geometric relationship described by this theorem.
Applications of Pythagoras Theorem
The Pythagorean theorem has numerous practical applications in various fields, including:
- Geometry and Trigonometry: It's fundamental in geometry and trigonometry for solving problems related to right triangles, such as calculating side lengths, angles, and distances.
- Construction and Architecture: Architects and builders use it to ensure right angles in structures, measure diagonals, and check for squareness in buildings.
- Surveying: Land surveyors use the theorem to calculate distances, establish right angles, and determine elevation changes.
- Engineering: Engineers apply it in designing structures, roads, and bridges, as well as in navigation systems and robotics for calculating distances.
- Astronomy: Astronomers use it for celestial navigation and to measure distances between stars and galaxies.
- Computer Graphics: In 3D computer graphics, it's used for calculating distances, angles, and perspective in rendering.
- Physics: Physicists use it for analyzing vectors, calculating velocities, and determining the magnitude of forces in vector addition.
- Optics: Opticians use it in lens design to calculate focal lengths and optical paths.
- Music: Musicians and acousticians apply it to understand the relationships between musical frequencies and harmonics.
- Finance: In financial modeling, it's used to calculate the distance between two points, such as interest rates or stock prices.
| Related Links | |
| Complex Number Division Formula | Probability |
| Probability formula | Consecutive Integers Formula |
Pythagorean Theorem Formula FAQs
Q1. What is the Pythagorean Theorem?
Q2. How is the Pythagorean Theorem formula expressed?
Q3. What is the hypotenuse of a right triangle?
Q4. Can the Pythagorean Theorem be applied to non-right triangles?
Q5. What is a Pythagorean Triple?










