Physics Wallah

RS Aggarwal Solutions Class 9 Maths Chapter 10 Quadrilaterals

Here, we have provided RS Aggarwal Solutions Class 9 Maths Chapter 10. Students can view these RS Aggarwal Solutions Class 9 Maths Chapter 10 before exams for better understanding of the chapter.
authorImageNeha Tanna10 Apr, 2024
Share

Share

RS Aggarwal Solutions Class 9 Maths Chapter 10

RS Aggarwal Solutions Class 9 Maths Chapter 10: Chapter 10 of Class 9 Maths by RS Aggarwal is based on quadrilateral characteristics. Common quadrilaterals include the square, rectangle, rhombus, kite, parallelogram, and so forth. You will study the foundational theorems based on quadrilateral properties in this chapter.

The RS Aggarwal Solutions Class 9 Maths Chapter 10 will assist you in comprehending the most effective methods of tackling quadrilateral sum problems. These activities have been completed by our highly qualified instructors. Get the PDF from here for free.

RS Aggarwal Solutions Class 9 Maths Chapter 10 PDF

The PDF that is provided below contains the solutions for RS Aggarwal Class 9 Maths Chapter 10 Quadrilaterals. All of the chapter's questions are answered in this PDF, which will aid in your understanding of the subjects. This resource can be very beneficial whether you're studying for an exam or just want to get your questions answered.

RS Aggarwal Solutions Class 9 Maths Chapter 10 PDF

RS Aggarwal Solutions Class 9 Maths Chapter 10

Below are the answers to RS Aggarwal Class 9 Maths Chapter 10 Quadrilaterals. These solutions make it simpler for students to comprehend and resolve number system-related issues by offering detailed explanations for every question in the chapter.

RS Aggarwal Solutions Class 9 Maths Chapter 10 Exercise 10.1

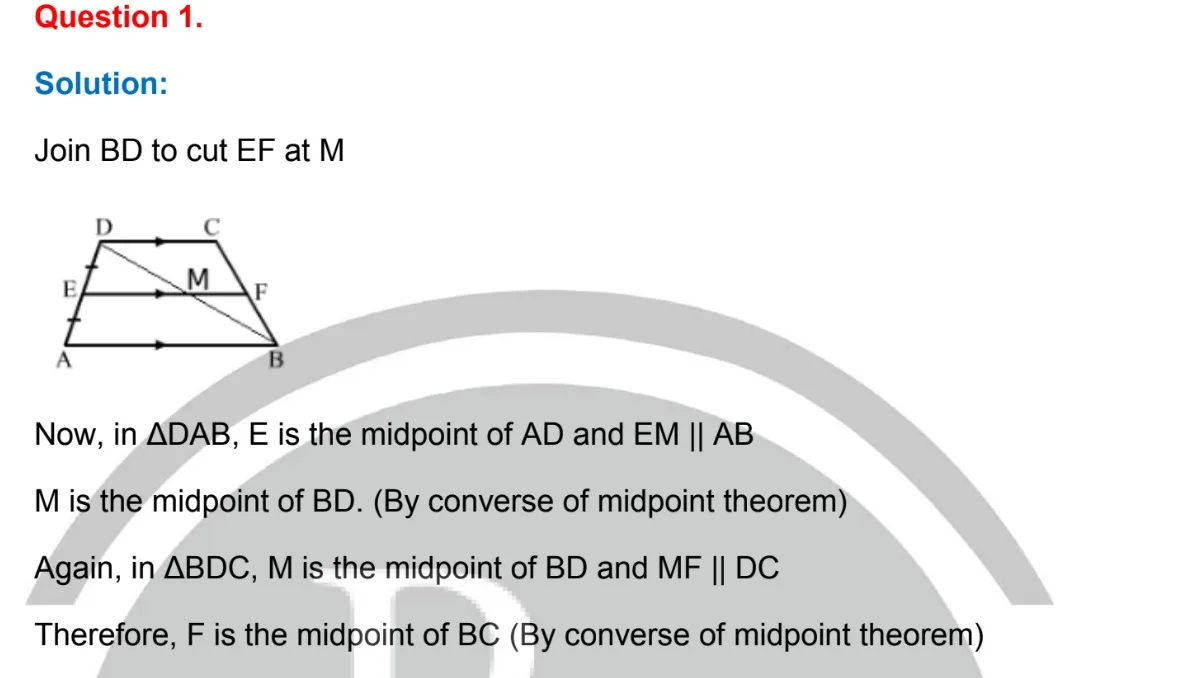
Question 1.

Solution:

Let, the measure of the fourth angle be X∘ Since the sum of the angle of a quadrilateral is 360∘, we have: 56 + 115 + 84 + X = 360 ⇒ 255 + X = 360 ⇒ X = 105 Hence, the measure of the fourth angle is 105.

Question 2.

Solution:

Let, ∠A = 2X Then ∠B=(4X) ∠C=(5X) and ∠D=(7X) Since the sum of the angles of a quadrilateral is 360∘, we have: 2X + 4X + 5X + 7X = 360 18X = 360∘ ⇒ X = 20∘ Therefore, Angle A = 40∘ Angle B = 80∘ Angle C = 100∘ Angle D = 140∘

Question 3.

Solution:

We have AB∥DC Angle A and Angle D are the interior angles on the same side of the transversal line AD, whereas angle B and Angle C are the same interior angles on the same side of transversal line BC. Now, Angle A + Angle D = 180∘ ⇒ ∠D = 180∘ – ∠A Therefore, ∠D = 180∘ – 55∘ = 125∘ Again, ∠B + ∠C = 180∘ ⇒ ∠C = 180∘ – ∠B Therefore, ∠C = 180∘ – 70∘ = 110∘

Question 4.

Solution:

ABCD is a square in which AB = BC = CD = DA. ΔEDC is an equilateral triangle in which ED = EC = DC ∠EDC = ∠DEC = ∠DCE = 60∘ . To prove: AE = BE and ∠DAE = 15∘ Proof: In ΔADE and ΔBCE, we have: AD = BC [Sides of a square] DE = EC [Sides of an equilateral triangle] ∠ADE = ∠BCE = 90∘ + 60∘ = 150∘ ΔADE ≅ ΔBCE i.e., AE = BE Now, ∠ADE = 150∘ DA = DC [Sides of a square] DC = DE [Sides of an equilateral triangle] So, DA = DE ΔADE and ΔBCE are isosceles triangles. i.e., ∠DAE = ∠DEA = 1/2(180∘−150∘) = 30∘/2 = 15∘

Question 5.

Solution:

A quadrilateral ABCD, in which BM ⊥ AC and DN ⊥ AC and BM = DN To prove: AC bisects BD, or DO = BO Proof: Let, AC and BD intersect at O Now, in ΔOND and ΔOMB, we have: ∠OND = ∠OMB (90∘ each) ∠DON = ∠BOM (Vertically opposite angles) Also, DN = BM (Given) i.e., ΔOND ≅ ΔOMB (AAS congruence rule) Therefore, OD = OB (CPCT) Hence, AC bisects BD

Question 6.

Solution:

Given: ABCD is a quadrilateral in which AB = AD and BC = DC (i) In ΔABC and ΔADC, we have: AB = AD (Given) BC = DC (Given) AC is common i.e., ΔABC ≅ ΔADC (SSS Congruence rule) Therefore, ∠BAC = ∠DAC and ∠BCA = ∠DCA (By CPCT) Thus, AC bisects ∠A and ∠C (ii) Now, in ΔABE and ΔADE, we have: AB = AD (Given) ∠BAE = ∠DAE (Proven above) AE is common. Therefore, ΔABE ≅ ΔADE (SAS congruence rule) ⇒ BE = DE (By CPCT) (iii) ΔABC ≅ ΔADC (Proven above) Therefore, Angle ABC = Angle ADC (By CPCT)

Question 7.

Solution:

Let, ABCD be a parallelogram ∠ A = ∠ C and ∠ B = ∠ D (Opposite angles) Let ∠ A be the smallest angle whose measure is x° ∴ ∠B = (2x – 30)° Now, ∠ A + ∠ B = 180° (Adjacent angles are supplementary) ⇒ x + 2x – 30° = 180° ⇒ 3x = 210° ⇒ x = 70° ∴ ∠B = 2 x 70°- 30° = 110° Hence, ∠ A = ∠ C = 70°; ∠ B = ∠ D = 110°
CBSE Class 9 Maths Syllabus CBSE Class 9 Science Syllabus
CBSE Class 9 Computer Application Syllabus CBSE Class 9 Social Science Syllabus

Question 8.

Solution:

Let, ABCD be a quadrilateral whose diagonals are AC and BD and O is any point within the quadrilateral Join O with A, B, C, and D We know that the sum of any sides of a triangle is greater than the third side So, in ΔAOC, OA + OC > AC Also, ΔBOD, OB + OD > BD Adding these inequalities, we get: (OA + OC) + (OB + OD) > (AC + BD) ⇒ OA + OB + OC + OD > AC + BD

Question 9.

Solution:

Given: ABCD is a quadrilateral and AC is one of its diagonals (i) In ΔABC, AB + BC > AC . . . . . . . . (1) In ΔACD, CD + DA > AC . . . . . . . . . . (2) Adding inequalities (1) and (2), we get: AB + BC + CD + DA > 2AC (ii) In ΔABC, we have : AB + BC > AC . . . . . . . . (1) We also know that the length of each side of a triangle is greater than the positive difference of the the other two sides. In ΔACD, we have: AC > |DA–CD| . . . . . . . (2) From (1) and (2), we have: AB + BC > |DA–CD| ⇒ AB + BC + CD > DA (iii) In ΔABC, AB + BC > AC In ΔACD, CD + DA > AC ΔBCD, BC + CD > BD ΔABD, DA + AB > BD Adding these inequalities, we get: 2 (AB + BC + CD + DA) > 2 (AC + BD) ⇒ (AB + BC + CD + DA) > (AC + BD)

Question 10.

Solution:

Let ABCD be a quadrilateral and ∠1, ∠2, ∠3 and ∠4 are its four angles as shown in the figure. Join BD which divides ABCD in two triangles, ΔABD and ΔBCD. In ΔABD, we have: ∠ 1 + ∠ 2 + ∠ A = 180° . . . . . . . . (i) In ΔBCD, we have: ∠ 3 + ∠ 4 + ∠ C = 180° . . . . . . . (ii) On adding (i) and (ii), we get: (∠1 + ∠3) + ∠A + ∠C + (∠ 4 + ∠2) = 360° ⇒ ∠ A + ∠ C + ∠ B + ∠ D = 360° (Since,∠ 1 + ∠ 3 = ∠ B; ∠ 4 + ∠ 2 = ∠ D) ∴ ∠ A + ∠ C + ∠ B + ∠ D = 360°

RS Aggarwal Solutions Class 9 Maths Chapter 10 Exercise 10.2

Question 6.

Solution:

Given : In ||gm ABCD, E is mid point of DC. EB is joined and through D, DEG || EB is drawn which meets CB produced at G and cuts AB at F. To prove : (i)AD = 1⁄2 GC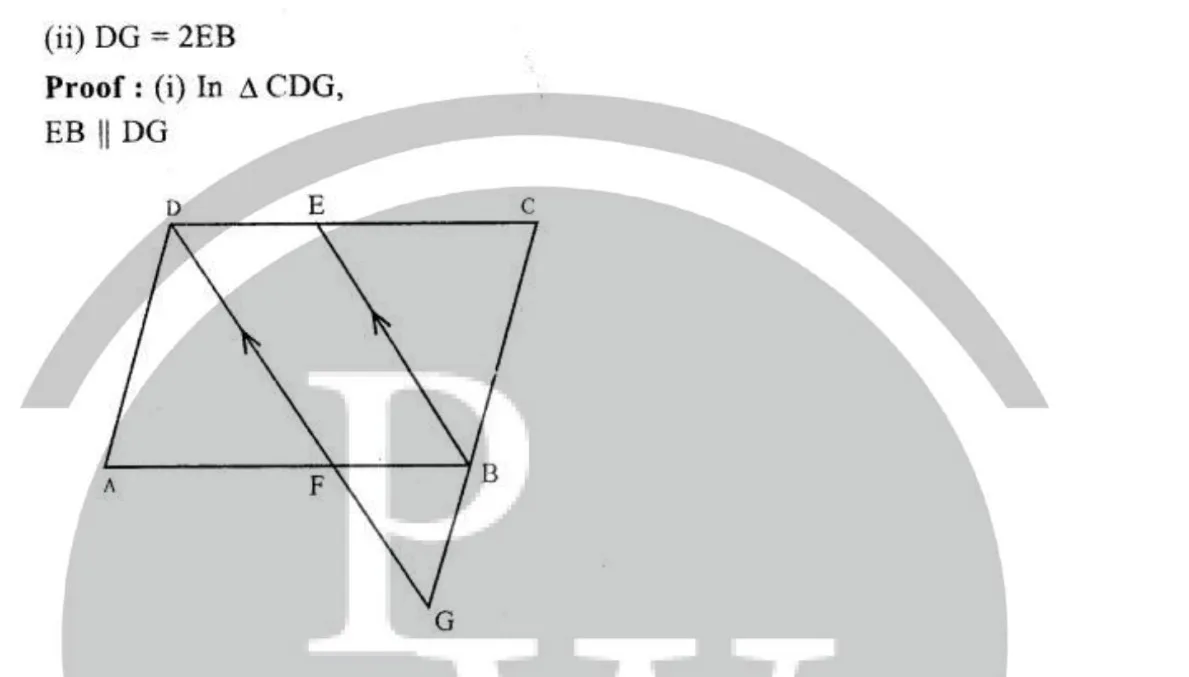

RS Aggarwal Solutions Class 9 Maths Chapter 10 Exercise 10.3

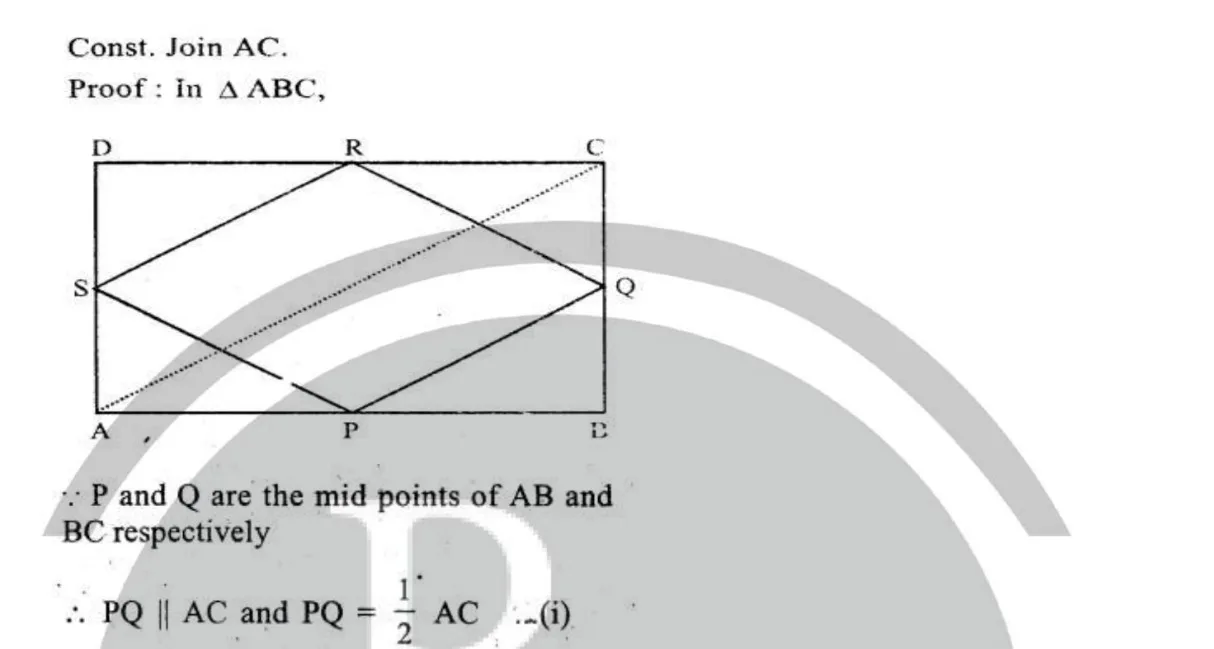
Question 2.

Solution:

In parallelogram ABCD, we have: AD || BC and AB || DC AD = BC and AB = DC AB = AE + BE and DC = DF + FC AE = BE = DF = FC Now, DF = AE and OF || AE. i.e., AEFD is a parallelogram. AD || EF Similarly, BEFC is also a parallelogram. EF || BC and AD || EF || BC Thus, AD, EF and BC are three parallel lines cut by the transversal line DC at D, F and C, respectively such that DF = FC. These lines AD, EF and BC are also cut by the transversal AB at A, E and B, respectively such that AE = BE Similarly, they are also cut by GH Therefore, GP = PH (By intercept theorem)

Question 3.

Solution:

Given: AB || DC, AP = PD and BQ = CQ (i) In ΔQCD and ΔQBE, we have: ∠DQC = ∠BQE (Vertically opposite angles) ∠DCQ = ∠EBQ (Alternate angles, as AE || DC) BQ = CQ (P is the midpoints) ΔQCD =ΔQBE Hence, DQ = QE (CPCT) (ii) Now, in ΔADE, P and Q are the midpoints of AD and DE, respectively. PQ || AE, PQ AB || DC and AB || PR || DC (iii) PQ AB and DC are the three lines cut by transversal AD at P such that AP = PD. These lines PQ, AB, DC are also cut by transversal BC at Q such that BQ = QC. Similarly, lines PQ, AB and DC are also cut by AC at R. Therefore, AR = RC (By intercept theorem).

Question 4.

Solution:

AD is a median of ΔABC and BD = DC We know that the line drawn through the midpoint of one side of a triangle and parallel to another side bisects the third side. Here, in ΔABC, D is the midpoint of BC and DE || BA (given). Then DE bisects AC. i.e., AE = EC E is the midpoint of AC Therefore, BE is the median of Δ ABC

Question 5.

Solution:

In ΔABC, we have: AC = AE + EC . . . . . . (i) AE = EC . . . . . . (ii) [BE is the median of ABDC] AC = 2EC . . . . . . . (iii) In Δ BEC, DF || BE. EF = CF (By midpoint theorem, as D is the midpoint of BC) But EC = EF + CF EC = 2 (CF) . . . . . . (iv) From (iii) and (iv), we get: AD = 12 GC In ADCG, DG || EB and E is the midpoint of DC and B is the midpoint of GC. By midpoint theorem, the line segment joining the mid points of any two sides of a triangle is parallel to the third side and is half of it. i.e., EB = 12DG DG = 2 (EB)

Question 6.

Solution:

Δ ABC is shown in the figure D, E and F are the midpoints of sides AB, BC and CA, respectively As, D and E are the mid points of sides AB, and BC of Δ ABC DE || AC (By midpoint theorem) Similarly, DF || BC and EF || AB Therefore, ADEF, BDFE, and DFCE are all parallelograms. Now, DE is the diagonal of the parallelogram BDFE. Δ BDE = Δ FED Similarly, DF is the diagonal of the parallelogram ADEF. Δ DAF = Δ FED And, EF is the diagonal of the parallelogram DFCE. Δ EFC = Δ FED. So, all the four triangles are congruent.

Question 7.

Solution:

Δ ABC is shown below. D, E and F are the midpoints of sides BC, CA and AB, respectively. As F and E are the mid points of sides AB and AC of Δ ABC. FE || BC (By mid point theorem) Similarly, DE || FB and FD || AC Therefore, AFDE, BDEF, and DCEF are all parallelograms. In parallelogram AFDE, we have: ∠A = ∠EDF (Opposite angles are equal) In parallelogram BDEF, we have: ∠B = ∠DEF (Opposite angles are equal) In parallelogram DCEF, we have: ∠C = ∠DFE (Opposite angles are equal)

Benefits of RS Aggarwal Solutions Class 9 Maths Chapter 10

This is the PDF for the RS Aggarwal Class 9 Maths Solutions. Students will gain a great deal from this in terms of timely revision and exam preparation. Before entering board class, pupils must complete a significant portion of their lives in class nine. Each chapter's solutions are given succinctly, and downloading the PDF offline to your PC is a helpful feature. One of the best things about this book is that it covers a wide range of problems, from easy, conceptual ones that don't require much thought to difficult ones that take a lot of the student's time. The difficult problems are answered in easy-to-understand steps with an explanation. As a result, this guarantees that students will learn a great deal from each question they answer and will boost their confidence for both current school tests and upcoming entrance examinations.

RS Aggarwal Solutions Class 9 Maths Chapter 10 FAQs

Which is better RS Aggarwal or RD Sharma?

Both RD Sharma and R.S. Aggarwal are reputable authors, and the choice between them often depends on personal preference and learning style. RD Sharma is known for its comprehensive approach, while R.S. Aggarwal is praised for its clear explanations and varied exercises.

How to study quadrilaterals Class 9?

First learn the basic properties and theorems.

Is RS Aggarwal important?

RS Aggarwal is one of the most important reference books for high school grades and is recommended to every highschool student.
Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
008448982616
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.