RS Aggarwal Solutions Class 9 Maths Chapter 13 Geometrical Constructions
Here, we have provided RS Aggarwal Solutions Class 9 Maths Chapter 13. Students can view these RS Aggarwal Solutions Class 9 Maths Chapter 13 before exams for better understanding of the chapter.
Neha Tanna12 Apr, 2024
Share
RS Aggarwal Solutions Class 9 Maths Chapter 13: Any student must take Class 9 since it provides the fundamental knowledge needed to advance to Class 10, which is why it is so important. Additionally, a student appears for his first national exam or board exam of his academic career after finishing the ninth and tenth grades. Therefore, RS Aggarwal Solutions Class 9 Maths Chapter 13 is here to practice your questions and make sense of the fundamental ideas.
After finishing the NCERT Maths, students must complete additional maths questions of various kinds. One cannot learn maths by memorization. Practice adding from different books as a result. This is where you can get assistance from RS Aggarwal Class 9 Answers Chapter 13. The questions focus on different building techniques by the chapter.RS Aggarwal Solutions Class 9 Maths Chapter 13
Using the above link, you can get the PDF for RS Aggarwal Solutions Class 9 Maths Chapter 13 solutions. All of the chapter's tasks have thorough solutions included in this PDF, which will improve your comprehension of these types of questions.RS Aggarwal Solutions Class 9 Maths Chapter 13 Geometrical Constructions
Question 1.
Solution:
Steps of Construction: (i) Draw a line segment AB = 5 cm (ii) With A as the centre and radius equal to more than half of AB, draw two arcs, one above AB and the other below AB. (iii) With B as a centre and the same radius draw two arcs which cut the previously drawn arcs at C and D. (iv) Join CD , intersecting AB at point P. ∴ CD is the perpendicular bisector of AB at the point P.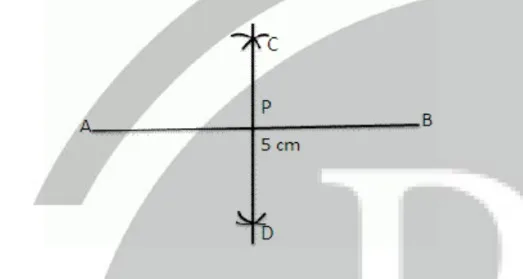
Question 2.
Solution:
Steps of construction. (ii) With A as the centre and with a small radius drawn arc cutting AB at P. (i) Draw a line segment AB. (iii) With P as a centre and the same radius draw another arc cutting the previous arc at Q and then R.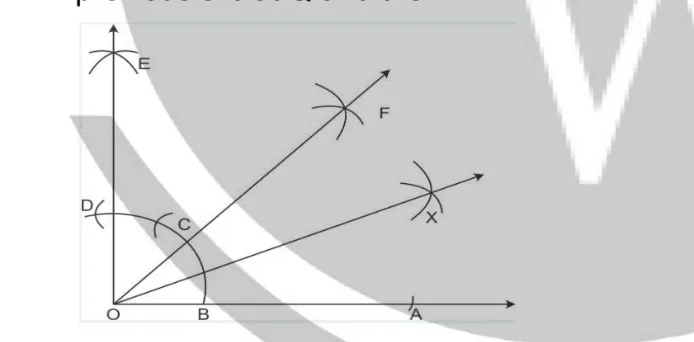
(iv) Bisect arc QR at S.
(v) Join AS and produce it to X such that ∠ BAX = 90°.
(vi) Now with centres P and S and with a suitable radius, draw two arcs
intersecting each other at T.
(vii) Join AT and produce it to C Then ∠BAC = 45°.
(viii) Again with centres P and T and suitable radius draw two arcs
intersecting each at D.
(ix) Join AD.
AD is the bisector of ∠ BAC
Question 3.
Solution:
Steps of construction. (i) Draw a line segment AB. (ii) With centre A and the same radius draw an arc which meets AB at P. (iii) With centre P and the same radius, draw arcs first at Q and then at R. (iv) With centres Q and R, draw arcs intersecting each other at C intersecting the first arc at T.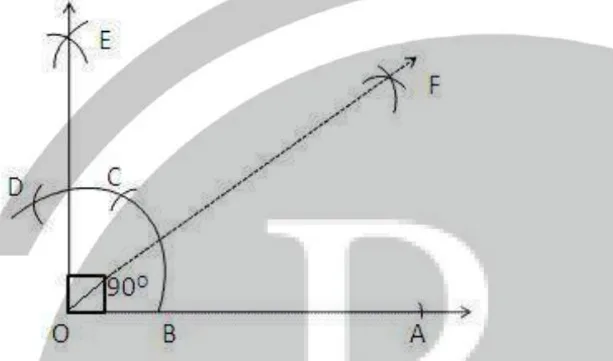
(v) Join AC
Then ∠BAC = 90°
(vi) Now with centres P and T and with some suitable radius, draw two
arcs intersecting each other at L.
(vii) Join AL and produce it to D.
Then AD is the bisector of ∠ BAC.
Question 4.
Solution:
Steps of construction. (i) Draw a line segment BC = 5cm. (ii) With centres B and C and radius 5cm, draw two arcs intersecting each other at A.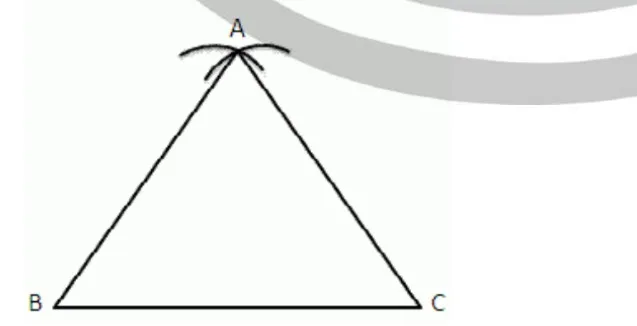
(iii) Join AB and AC.
Then ∆ ABC is the required equilateral triangle.
Question 5.
Solution:
We know that altitudes of equilateral triangles are equal and each angle is 60°. Steps of construction. (i) Draw a line XY and take a point D on it. (ii) At D, draw a perpendicular and cut off DA = 5.4cm.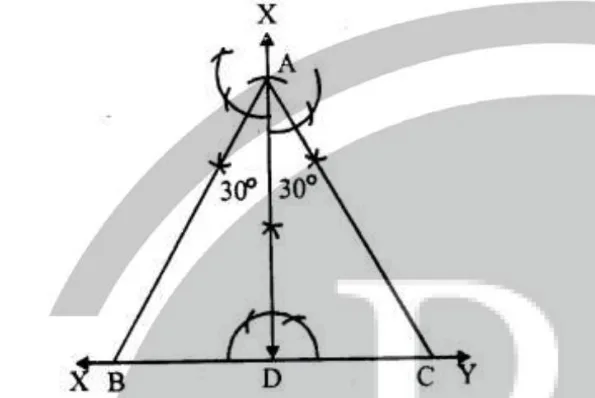
(iii) At A draw angles of 30° on each side of AD which meet XY at B and
C respectively.
Then ∆ ABC is the required triangle.
Question 6.
Solution:
Steps of construction : (i) Draw a line segment BC = 5cm (ii) With centre B and a radius of 3.8 cm draw an arc.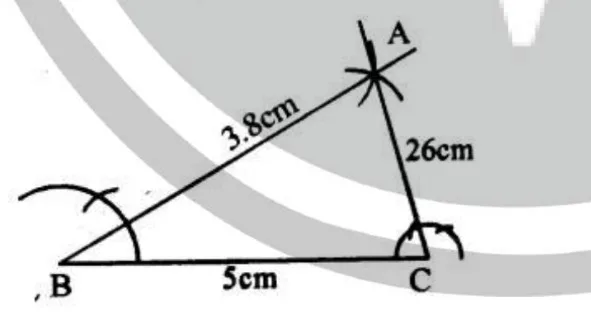
(iii) With centre C and a radius of 2.6 cm draw another arc intersecting the
first arc at A.
(iv) Join AB and AC.
Then ∆ ABC is the required triangle.
Question 7.
Solution:
Steps of construction : (i) Draw a line segment BC = 4.7cm. (ii) At B, draw a ray BX making an angle of 60° with BC.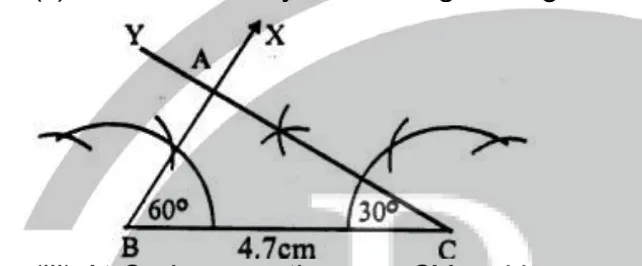
(iii) At C, draw another ray, CY making an angle of 30° which intersects
the ray BX at A ,
Then ∆ ABC is the required triangle On measuring ∠ A, it is 90°.
Question 8.
Solution:
Steps of Construction : (i) Draw a line segment QR * 5cm. (ii) With centres Q and R and a radius equal to 4.5cm, draw arcs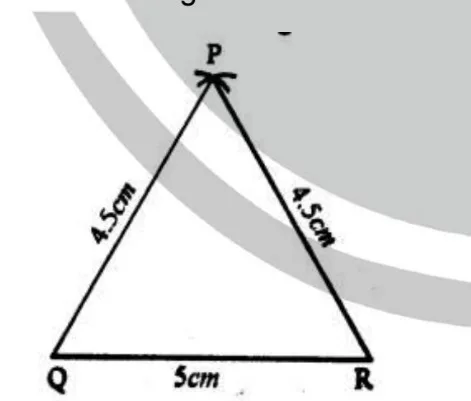
(iii) Join PQ and PR.
Then ∆ PQR is the required triangle.
Question 9.
Solution:
Steps of construction: (i) Draw a line segment BC = 4.5cm. (ii) At B, draw a ray BX making an angle of 90° with BC.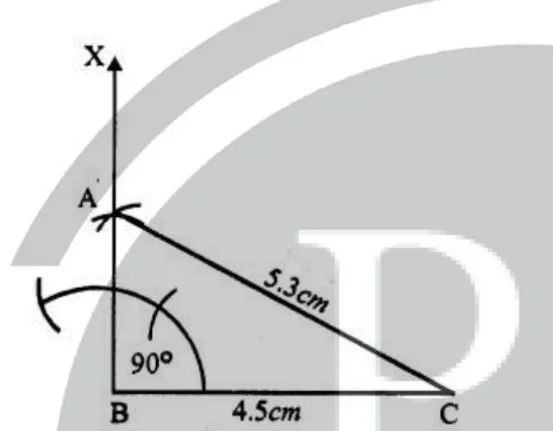
(iii) With centre C and radius 5.3 cm, draw an arc intersecting BX at A.
(iv) Join AC.
Then ∆ ABC is the required right-angled triangle.
Question 10.
Solution:
Steps of Constructions : (i) Draw a line segment BC = 5.2 cm. (ii) At B draw a ray BX making an angle of 30°.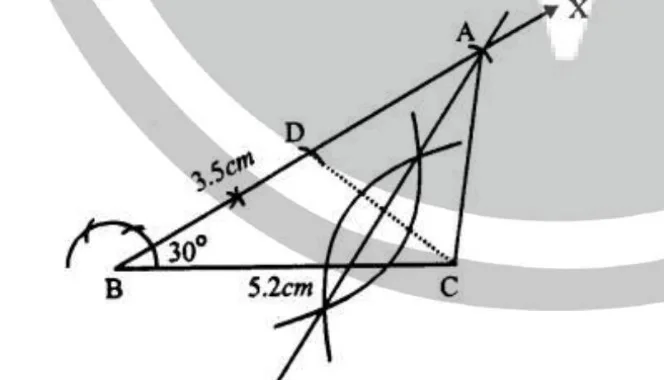
(iii) From BX, cut off BD = 3.5cm.
(iv) Join DC.
(v) Draw a perpendicular bisector of DC which intersects BX at A.
(vi) Join AC.
Then ∆ ABC is the required triangle.
Benefits of RS Aggarwal Solutions Class 9 Maths Chapter 13
Students should familiarise themselves with RS Aggarwal Class 9 Maths Chapter 13, which has been created by seasoned educators across India. It will answer all of your questions in the lead-up to the test. You can write an answer to get full marks by following the steps in the RS Aggarwal answers for Class 9 Maths, Chapter 13. The chapter is explained in simple terms so that everyone can understand it. You can identify the areas of the construction that require extra attention. The most effective way for a student to review every idea before the test is to use the RS Aggarwal Chapter 13 Maths Class 9. All solutions are provided in a step-by-step manner to help students comprehend them better.| CBSE Class 9 Maths Syllabus | CBSE Class 9 Science Syllabus |
| CBSE Class 9 Computer Application Syllabus | CBSE Class 9 Social Science Syllabus |
RS Aggarwal Solutions Class 9 Maths Chapter 13 FAQs
Which is better RS Aggarwal or RD Sharma?
RD Sharma is known for its comprehensive approach, while R.S. Aggarwal is praised for its clear explanations and varied exercises.
Is RS Aggarwal important?
RS Aggarwal is one of the most important reference books for high school grades and is recommended to every high school student.
Is RS Aggarwal tough?
This book has introductory, level 1, level 2 and level 3 exercises (easy to hard). Agarwal is good for practise only and provided conventional methods instead shortcuts/solving concept based. No concepts are explained before you start the chapter.
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.