
The trajectory formula serves to determine the flight path of an object in motion under the influence of gravity. It's particularly applicable to projectiles or celestial bodies. For Example, when a stone is thrown, its path approximates a parabola.
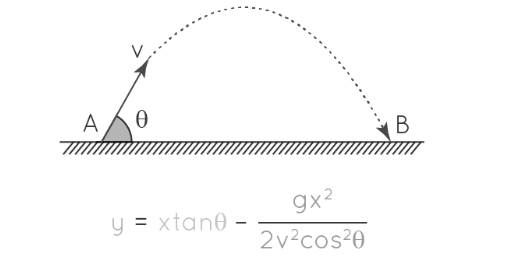
This formula precisely describes the trajectory:
y=xtanθ− gx 2 / 2v 2 cos 2 θ
Here are the variables: θ represents the projection angle from the horizontal. v denotes the initial velocity. g stands for the acceleration due to gravity. y is the vertical component. x is the horizontal component.
This formula allows the prediction of the projectile's path based on the initial motion values, enabling accurate projections without the necessity of observing the actual path of the object. To comprehend it better, let's explore solved examples using the trajectory formula.
Trajectory Formula Solved Examples
Example 1: Suppose a boy throws a stone with an initial velocity of 6 m/s at an angle of 60∘. Determine the equation of the projectile's path using g = 9.8 m/s^2 and the trajectory formula.
Solution: Given: θ = 60∘, v (initial velocity) = 6 m/s Utilizing the trajectory formula,y=xtan(θ)− gx 2 / 2v 2 cos 2 (θ)
Substituting the values: y=xtan60− 9.8x 2 / 2×6 2 ×cos 2 60 y=x√3−0.544x 2 Therefore, the equation for the projectile's trajectory is y=x√3−0.544x 2 .Example 2: Trevor strikes a ball with an initial velocity of 45 m/s. The far end of the field in the ball's direction of travel is 140.0 m away. If the initial angle of projection is 66.4°, determine the vertical height when the ball reaches the field's end using the trajectory formula.
Solution: Given: θ = 66.4°, v = 45 m/s, x = 140.0 m Using the trajectory formula,y=xtanθ− gx 2 / 2v 2 cos 2 θ
y=(140)tan66.4°− 9.8×140×140 / 2×45 2 ×cos 2 66.4° y=320.6− 192080 / 648 y=320.6−296.4=24.2 The vertical height when the ball reaches the end of the field is 24.2 m.Example 3: Suppose a boy throws a stone with an initial velocity of 3 m/s at an angle of 60∘. Determine the equation of the projectile's path using g = 9.8 m/s^2 and the trajectory formula.
Solution: Given: θ = 60∘, v (initial velocity) = 6 m/s Utilizing the trajectory formula,y=xtanθ− gx 2 / 2v 2 cos 2 θ
Substituting the values: y=xtan60− 9.8x 2 / 2×3 2 ×cos 2 60 y=x√3− 1.089x 2 Therefore, the equation for the projectile's trajectory is y=x√3−0.544x 2 .These Solved examples demonstrate the practical application of this formula in determining the path of projectiles thrown at certain angles with specific initial velocities, showcasing how it aids in calculating the vertical and horizontal components of an object's path.
When an object is thrown at an angle relative to the horizontal direction, it traces a curved path in the shape of a parabola, known as a projectile trajectory.Understanding the trajectory formula is crucial in predicting the path of objects influenced by gravity, such as projectiles or celestial bodies. This formula, y=xtanθ− gx 2 / 2v 2 cos 2 θ , encapsulates the relationships between key variables: the projection angle ( θ), initial velocity ( v), acceleration due to gravity ( g), and the components of horizontal ( x) and vertical (y) motion.
By utilizing this formula, it becomes possible to accurately forecast the trajectory of an object in motion, bypassing the necessity of observing its actual path.
The trajectory formula serves as a fundamental tool in physics and mathematics, enabling the precise prediction of an object's flight path, contributing to various fields such as ballistics, astronomy, and mechanics.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| Foil Formula | Function Notation Formula |
| Hexagonal Pyramid Formula | Hypothesis Testing Formula |
Trajectory Formula FAQs
What does the trajectory formula determine?
What does the equation y = x tan(θ) - (gx^2) / (2v^2 cos^2 θ) represent?
What are the key variables in the trajectory formula?
How does the formula aid in predicting object paths?










