Uniform Distribution Formula, Definition, Solved Examples

Uniform Distribution Formula: A continuous probability distribution known as the uniform distribution represents events that have an equal likelihood of occurring. This distribution is characterized by two parameters, 'a' and 'b', where 'a' stands for the minimum value and 'b' denotes the maximum value, typically represented as u(a, b). Visually, the probability density function is depicted as a rectangle with a base of (b - a) and a height of 1 / (b - a). Exploring the uniform distribution formula in further detail will offer a deeper understanding of its principles.

Uniform Distribution Formula

The uniform distribution formula defines the probability density function for a continuous random variable X within a uniform distribution as f(x) = 1 / (b - a). Represented as U(a, b), where 'a' and 'b' are constants such that 'a' is the minimum value and 'b' is the maximum value, and for which a ≤ x ≤ b.

In this equation:

'a' signifies the minimum value.

'b' represents the maximum value.

This probability distribution function can be expressed as:

f(x) = 1 / (b - a) for a ≤ x ≤ b.

Moreover, when considering the mean (μ) and variance (σ^2), the probability density can be redefined in terms of these statistical measures.

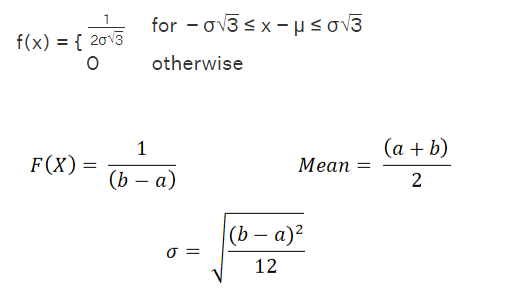
Uniform Distribution Formula Solved Examples

Example 1: Uniform Probability Density Function and Function Height

In the case of a uniform probability density function, the function's height:

1. Varies for different values of x
2. Decreases as x increases
3. Remains constant for each value of x

Solution:

A uniform probability distribution function, as implied by its name, refers to a symmetrical and uniform distribution for a finite continuous variable dataset. This distribution possesses a flat probability density where the area under the curve equals 1. In this scenario, the mean is equal to the median, and all values within the distribution are equally probable.

Hence, for a uniform probability density function, the height of the function remains consistent for each value of x.

Answer: c. Remains constant for each value of x

Example 2: Applying the Uniform Probability Density Function to a Random Variable Given a random variable X ~ (0, 23) according to a uniform probability density function, determine P(2 < X < 20).

Solution:  P(2 < X < 20)=    (20−2)⋅ 1/23−0 ​ =  18 / 23 ​

The uniform distribution, characterized by equal probability of events within a specified range, is represented by the U(a, b) formula, where 'a' and 'b' designate the minimum and maximum values, respectively. Its probability density function, f(x)=1/ b−a  ​ , illustrates the uniform nature of this distribution, ensuring that all values within the range have the same probability of occurring.

Understanding the uniform distribution provides insight into the consistent nature of probabilities across its range. In scenarios where the distribution exhibits an even and symmetrical pattern, the probability density function remains constant for each value of 'x'. This uniformity makes it easier to calculate probabilities within the distribution, such as determining the likelihood of specific intervals.

The uniform distribution offers a straightforward model for scenarios where events have an equal chance of occurring within a defined range, making it a fundamental concept in probability theory and statistics. Its formula and properties simplify the analysis of probabilities for continuous random variables with consistent and predictable outcomes.

Uniform Distribution Formula Key Points

Uniform distribution in statistics ensures equal probability for all outcomes.

Also termed as a rectangle distribution, it maintains a constant value within its range.

There are two types: discrete and continuous uniform distributions.

It provides a straightforward graphical representation, either in graph form or as a list.

Examples of uniform distributions include rolling a die or tossing a coin.