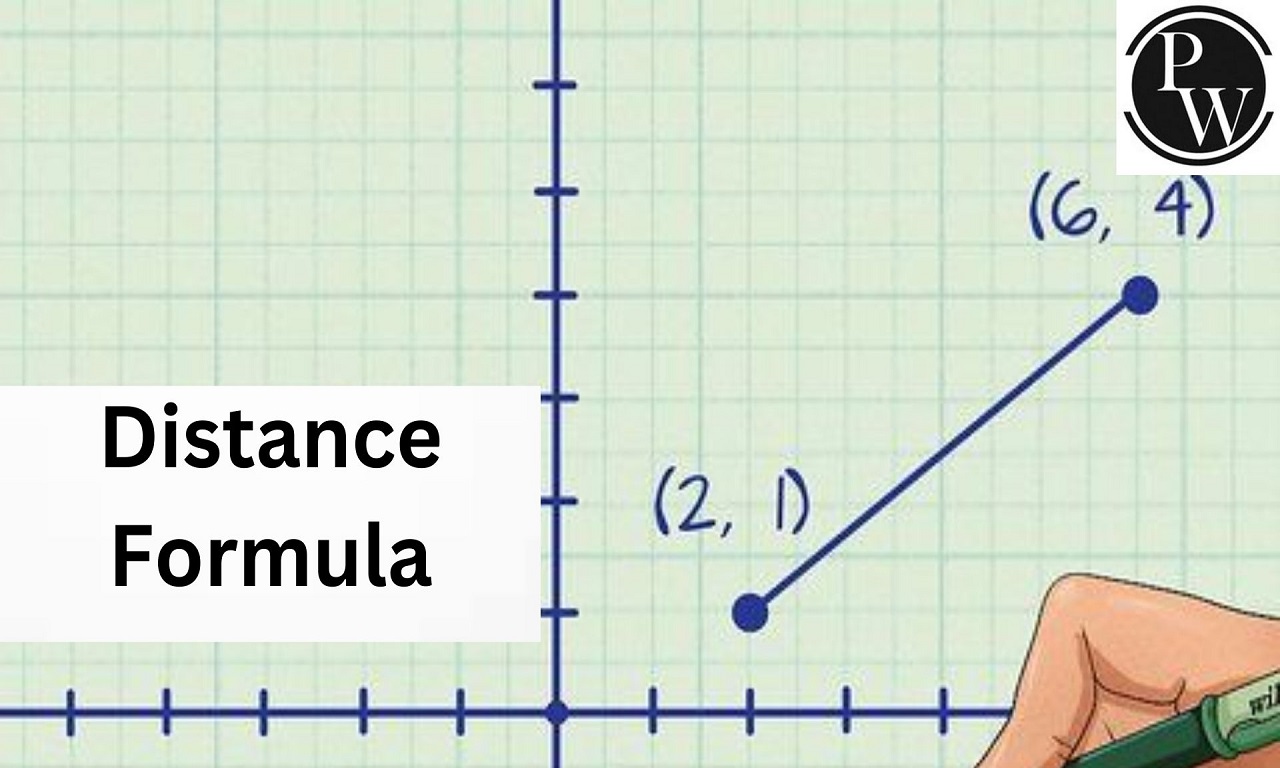
The Distance Formula, frequently encountered in Class 10 mathematics, serves to compute the distance between two points in coordinate geometry. Understanding its fundamental concepts is crucial, given its significance in various applications, such as estimating distances between moving objects or locations. List of Distance Formulas for Class 10:
Distance between Points (x
1
, y
1
) and (x
2
, y
2
):
D=[ (x
2
−x
1
)
2
+(y
2
−y
1
)
2
]
1/2
Distance of a Point P(x, y) from the Origin O(0,0):
D= (x
2
+y
2
)
Coordinates of a Point dividing Line Segment AB(x
1
, y
1
) and B(x
2
, y
2
) in ratio m
1
: m
2
:
( (m
1
x
2
+m
2
x
1
) /(m
1
+m
2
) , (m
1
y
2
+m
2
y
1
) /(m
1
+m
2
) )
Midpoint of Line Segment AB(x
1
, y
1
) and B(x
2
, y
2
):
( (x
1
+x
2
)/2 , ( y
1
+y
2
)/2 )
Applications of Distance Formula
The distance formula finds applications in both algebra and geometry: Navigation systems utilize the distance formula, derived from Pythagoras' theorem, to determine coordinates on sea and land, forming an integral part of navigation technology. In coordinate geometry, it aids in identifying the shape of a given quadrilateral. If the sides are equal, it implies a square. Additionally, it's instrumental in finding the shortest path between two points.
Distance Formula Solved Examples
Example 1:
Use the distance formula to find the distance between points P(-5,7) and Q(-1,3).
Solution:
Distance between Points (x
1
, y
1
) and (x
2
, y
2
):
D=[ (x
2
−x
1
)
2
+(y
2
−y
1
)
2
]
1/2
D= (−1−(−5))
2
+(3−7)
2
= 4
2
+(−4)
2
= 32
Example 2:
Determine the coordinates of the point dividing the line segment joining (4, –2) and (7, 4) in the ratio 2:1 internally.
Solution: Let the coordinates be (x, y).
x= (m
1
x
2
+m
2
x
1
) / m
1
+m
2
= 3 4∗2+7∗1 =5
y= ( m
1
y
2
+m
2
y
1
) / m
1
+m
2
= 3 −2∗2+4∗1 =0
Hence, the coordinates are (5, 0).
Strategies for Memorizing the Distance Formula
Mastering the distance formula in Class 10 is pivotal for problem-solving. Employ these straightforward tips to aid in memorization:
Comprehensive Understanding: Grasp all concepts linked to the Class 10 distance formula. This knowledge base will facilitate logical application of the formula across diverse problems.
Practice Problem-Solving: Engage in solving a multitude of problems that revolve around the distance formula. Regular practice enhances comprehension and the ability to apply the formula effectively in various scenarios.
Utilize Online Resources: Explore internet resources such as formula sheets. These materials are readily available for learning and revision. Downloading formula sheets onto mobiles, tablets, or laptops enables convenient revision at any time.
Distance Formula is a crucial tool in Class 10 mathematics, allowing for the calculation of distances between points in coordinate geometry. Mastering its fundamental concepts and formulas is vital due to its wide-ranging applications, from estimating distances between moving objects to aiding in navigation systems on both land and sea.
The formulas for calculating distances between points, from a point to the origin, dividing line segments, and finding midpoints serve as fundamental tools. These formulas find practical use not only in algebra and geometry but also in real-world scenarios, determining shapes of quadrilaterals and establishing the shortest path between two points.
To effectively grasp and apply the Distance Formula, a comprehensive understanding of its concepts, regular practice in problem-solving, and utilization of online resources such as formula sheets are essential strategies. These strategies aid in memorization and practical application, ensuring proficiency in using the Distance Formula across various scenarios in mathematics.
Explore Now Online Course of Class 9
Neev Fastrack 2024
and Class 10
Udaan Fastrack 2024
to enhance your Maths knowledge. and build a strong foundation.
