NCERT Solutions for Class 12 Chemistry Chapter 2 Solutions
NCERT Solutions for Class 12 Chemistry Chapter 2 Solutions contains all the questions with detailed solutions. Students are advised to practice these questions for better understanding of the concepts given in the chapter.
Krati Saraswat21 Aug, 2025
Share
NCERT Solutions for Class 12 Chemistry Chapter 2: NCERT Solutions for Class 12 Chemistry Chapter 2, Solutions, provide a detailed explanation of important concepts such as types of solutions, solubility, Raoult’s law, colligative properties, and abnormal molar masses. These solutions are designed as per the latest CBSE syllabus and cover all essential topics required for board exams.
The CBSE exam pattern includes a mix of theoretical and numerical questions, with a focus on concept-based short and long-answer questions, as well as numerical problems based on colligative properties. Solving previous year questions (PYQs) helps students understand frequently asked topics and improve their problem-solving skills. These solutions are an excellent resource for board exam preparation and competitive exams like JEE and NEET.
NCERT Solutions for Class 12 Chemistry Chapter 1
NCERT Solutions for Class 12 Chemistry Chapter 2 Overview
NCERT Solutions for Class 12 Chemistry Chapter 2 cover several important topics. It is highly recommended for students to review each topic thoroughly in order to gain a comprehensive understanding of the concepts taught in the chapter and make optimal use of the provided solutions. These solutions are the result of dedicated efforts by the Physics Wallah teachers aimed at assisting students in grasping the concepts covered in this chapter. By going through and practicing these solutions, the objective is for students to achieve excellent results in their exams effortlessly.NCERT Solutions for Class 12 Chemistry Chapter 2
Answer the following Questions of NCERT Solutions for Class 12 Chemistry Chapter 2:
Question 1. Calculate the mass percentage of benzene (C 6 H 6 ) and carbon tetrachloride (CCl 4 ) if 22 g of benzene is dissolved in 122 g of carbon tetrachloride. Solution : Mass percentage of C 6 H 6
Mass percentage of CCl 4 
Alternatively, Mass percentage of CCl 4 = (100 − 15.28)% = 84.72%
Question 2. Calculate the mole fraction of benzene in solution containing 30% by mass in carbon tetrachloride. 
= 0.3846 mol Molar mass of carbon tetrachloride (CCl 4 ) = 1 × 12 + 4 × 35.5 = 154 g mol −1 ∴Number of moles of CCl 4 = 70 / 154 = 0.4545 mol Thus, the mole fraction of C 6 H 6 is given as: 
= 0.458Solution : Molarity is given by:
(a) Molar mass of Co (NO 3 ) 2 .6H 2 O = 59 + 2 (14 + 3 × 16) + 6 × 18 = 291 g mol −1 ∴Moles of Co (NO 3 ) 2 .6H 2 O 
= 0.103 mol Therefore, molarity 
= 0.023 M (b) Number of moles present in 1000 mL of 0.5 M H 2 SO 4 = 0.5 mol ∴Number of moles present in 30 mL of 0.5 M H 2 SO 4 
= 0.015 mol Therefore, molarity 
= 0.03 M
Question 4. Calculate the mass of urea (NH 2 CONH 2 ) required in making 2.5 kg of 0.25 molal aqueous solution.
= 36.95 g = 37 g of urea (approximately) Hence, mass of urea required = 37 g Question 5. Calculate (a) molality (b) molarity and (c) mole fraction of KI if the density of 20% (mass/mass) aqueous KI is 1.202 g mL -1. 
= 1.506 m = 1.51 m (approximately) (b) It is given that the density of the solution = 1.202 g mL −1 ∴Volume of 100 g solution 
= 83.19 mL = 83.19 × 10 −3 L Therefore, molarity of the solution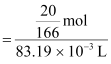 
= 1.45 M (c) Moles of KI 
Moles of water 
Therefore, mole fraction of KI 
= 0.0263 Question 6. H 2 S, a toxic gas with rotten egg like smell, is used for the qualitative analysis. If the solubility of H 2 S in water at STP is 0.195 m, calculate Henry’s law constant. 
= 55.56 mol ∴Mole fraction of H 2 S, x 
= 0.0035 At STP, pressure (p) = 0.987 bar According to Henry’s law: p = K H x 
= 282 bar
= 2.5 atm = 2.5 × 1.01325 × 10 5 Pa = 2.533125 × 10 5 Pa According to Henry’s law: 
= 0.00152 We can write, 
[Since, 
is negligible as compared to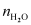 
] In 500 mL of soda water, the volume of water = 500 mL [Neglecting the amount of soda present] We can write: 500 mL of water = 500 g of water nH 2 0= 27.78 mol of water Now, 
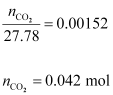Hence, quantity of CO 2 in 500 mL of soda water = (0.042 × 44)g = 1.848 g
= 450 mm of Hg 
= 700 mm of Hg p total = 600 mm of Hg From Raoult’s law, we have: 
Therefore, total pressure, 
Therefore, 
= 1 − 0.4 = 0.6 Now, 
= 450 × 0.4 = 180 mm of Hg 
= 700 × 0.6 = 420 mm of Hg Now, in the vapour phase: Mole fraction of liquid A 
= 0.30 And, mole fraction of liquid B = 1 − 0.30 = 0.70
= 23.8 mm of Hg Weight of water taken, w 1 = 850 g Weight of urea taken, w 2 = 50 g Molecular weight of water, M 1 = 18 g mol −1 Molecular weight of urea, M 2 = 60 g mol −1 Now, we have to calculate vapour pressure of water in the solution. We take vapour pressure as p 1 . Now, from Raoult’s law, we have: 
Hence, the vapour pressure of water in the given solution is 23.4 mm of Hg and its relative lowering is 0.0173.
= 121.67 g (approximately) Hence, 121.67 g of sucrose is to be added. Question 11. Calculate the mass of ascorbic acid (Vitamin C, C 6 H 8 O 6 ) to be dissolved in 75 g of acetic acid to lower its melting point by 1.5°C. K f = 3.9 K kg mol −1. Solution : Mass of acetic acid, w 1 = 75 g Molar mass of ascorbic acid (C 6 H 8 O 6 ), M 2 = 6 × 12 + 8 × 1 + 6 × 16 = 176 g mol −1 Lowering of melting point, ΔT f = 1.5 K We know that: 
= 5.08 g (approx) Hence, 5.08 g of ascorbic acid is needed to be dissolved. Question 12. Calculate the osmotic pressure in pascals exerted by a solution prepared by dissolving 1.0 g of polymer of molar mass 185,000 in 450 mL of water at 37°C. Solution : It is given that: Volume of water, V = 450 mL = 0.45 L Temperature, T = (37 + 273)K = 310 K Number of moles of the polymer, 
We know that: Osmotic pressure, 
= 30.98 Pa = 31 Pa (approximately)
Mole fraction is denoted by ‘x’. If in a binary solution, the number of moles of the solute and the solvent are n A and n B respectively, then the mole fraction of the solute in the solution is given by, 
Similarly, the mole fraction of the solvent in the solution is given as: 
(ii) Molality Molality (m) is defined as the number of moles of the solute per kilogram of the solvent. It is expressed as: Molality (m) 
(iii) Molarity Molarity (M) is defined as the number of moles of the solute dissolved in one Litre of the solution. It is expressed as: Molarity (M) 
(iv) Mass percentage: The mass percentage of a component of a solution is defined as the mass of the solute in grams present in 100 g of the solution. It is expressed as: Mass % of a component 
Question 15. Concentrated nitric acid used in laboratory work is 68% nitric acid by mass in aqueous solution. What should be the molarity of such a sample of the acid if the density of the solution is 1.504 g mL −1?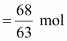 
= 1.079 mol Given, Density of solution = 1.504 g mL −1 (Mass / Density) = Volume of 100 g solution = 
Molarity of solution 
= 0.056 mol ⇒ Molality of solution 
= 0.62 m Number of moles of water 
= 5 mol ⇒ Mole fraction of glucose 
And, mole fraction of water 
= 1 − 0.011 = 0.989 If the density of the solution is 1.2 g mL −1 , then the volume of the 100 g solution can be given as: 
⇒ Molarity of the solution 
= 0.67 M
Molar mass of NaHCO 3 = 1 × 23 + 1 × 1 × 12 + 3 × 16 = 84 g mol −1 ⇒ Number of moles of NaHCO 3 
According to the question, 
⇒ 84x = 106 − 106x ⇒ 190x = 106 ⇒ x = 0.5579 Therefore, number of moles of Na 2 CO 3 
= 0.0053 mol And, number of moles of NaHCO 3 
= 0.0053 mol HCl reacts with Na 2 CO 3 and NaHCO 3 according to the following equation. 
1 mol of Na 2 CO 3 reacts with 2 mol of HCl. Therefore, 0.0053 mol of Na 2 CO 3 reacts with 2 × 0.0053 mol = 0.0106 mol. Similarly, 1 mol of NaHCO 3 reacts with 1 mol of HCl. Therefore, 0.0053 mol of NaHCO 3 reacts with 0.0053 mol of HCl. Total moles of HCl required = (0.0106 + 0.0053) mol = 0.0159 mol In 0.1 M of HCl, 0.1 mol of HCl is preset in 1000 mL of the solution. Therefore, 0.0159 mol of HCl is present in 
= 159 mL of the solution Hence, 159 mL of 0.1 M of HCl is required to react completely with 1 g mixture of Na 2 CO 3 and NaHCO 3, containing equimolar amounts of both.
= 75 + 160 = 235 g Total amount of solution = 300 + 400 = 700 g Therefore, mass percentage (w/w) of the solute in the resulting solution, 
= 33.57% And, mass percentage (w/w) of the solvent in the resulting solution, = (100 − 33.57)% = 66.43%
= 2 × 12 + 6 × 1 + 2 ×16 = 62 gmol −1 Number of moles of ethylene glycol 
= 3.59 mol Therefore, molality of the solution 
= 17.95 m Total mass of the solution = (222.6 + 200) g = 422.6 g Given, Density of the solution = 1.072 g mL −1 ⇒ Volume of the solution 
= 394.22 mL = 0.3942 × 10 −3 L ∴ Molarity of the solution 
= 9.11 M
= 1.5 × 10 −3 % (ii) Molar mass of chloroform (CHCl 3 ) = 1 × 12 + 1 × 1 + 3 × 35.5 = 119.5 g mol −1 Now, according to the question, 15 g of chloroform is present in 10 6 g of the solution. i.e., 15 g of chloroform is present in (10 6 − 15) ≈ 106 g of water. ∴ Molality of the solution 
= 1.26 × 10 −4 m 
Therefore, when the temperature is increased, heat is supplied and the equilibrium shifts backwards, thereby decreasing the solubility of gases. Question 23. State Henry’s law and mention some important applications? Solution : Henry’s law states that partial pressure of a gas in the vapour phase is proportional to the mole fraction of the gas in the solution. If p is the partial pressure of the gas in the vapour phase and x is the mole fraction of the gas, then Henry’s law can be expressed as: p = K H x Where, K H is Henry’s law constant Some important applications of Henry’s law are mentioned below.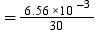
= 2.187 × 10 −4 mol Let the number of moles of the solvent be x. According to Henry’s law, p = K H x 
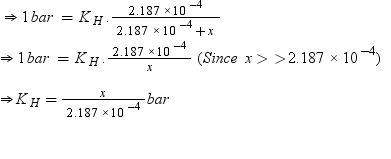Number of moles present in 5.00 × 10 −2 g of ethane 
= 1.67 × 10 −3 mol According to Henry’s law, p = K H x = 7.636 bar Hence, partial pressure of the gas shall be 7.636 bar.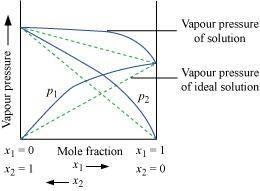
Vapour pressure of a two-component solution showing positive deviation from Raoult’s law 
Vapour pressure of a two-component solution showing negative deviation from Raoult’s law In the case of an ideal solution, the enthalpy of the mixing of the pure components for forming the solution is zero. Δ sol H = 0 In the case of solutions showing positive deviations, absorption of heat takes place. ∴Δ sol H = Positive In the case of solutions showing negative deviations, evolution of heat takes place. ∴Δ sol H = Negative Question 26. An aqueous solution of 2% non-volatile solute exerts a pressure of 1.004 bar at the normal boiling point of the solvent. What is the molar mass of the solute? 
Mass of solute, (w 2 ) = 2 g Mass of solvent (water), (w 1 ) = 98 g Molar mass of solvent (water), (M 1 ) = 18 g mol −1 According to Raoult’s law, 
= 41.35 g mol −1 Hence, the molar mass of the solute is 41.35 g mol −1. 
Vapour pressure of octane 
= 46.8 kPa We know that, Molar mass of heptane (C 7 H 16 ) = 7 × 12 + 16 × 1 = 100 g mol −1 ∴ Number of moles of heptane 
= 0.26 mol Molar mass of octane (C 8 H 18 ) = 8 × 12 + 18 × 1 = 114 g mol −1 ∴ Number of moles of octane = 35 /114 mol = 0.31 mol Mole fraction of heptane, 
= 0.456 And, mole fraction of octane, x 2 = 1 − 0.456 = 0.544 Now, partial pressure of heptane, 
= 0.456 × 105.2 = 47.97 kPa Partial pressure of octane, 
= 0.544 × 46.8 = 25.46 kPa Hence, vapour pressure of solution, p total = p 1 + p 2 = 47.97 + 25.46 = 73.43 kPa
= 55.56 mol Therefore, mole fraction of the solute in the solution is 
. It is given that, Vapour pressure of water, 
= 12.3 kPa Applying the relation, 
⇒ 12.3 − p 1 = 0.2177 ⇒ p 1 = 12.0823 = 12.08 kPa (approximately) Hence, the vapour pressure of the solution is 12.08 kPa. Then, the vapour pressure of the octane after dissolving the non-volatile solute is 
Molar mass of solute, M 2 = 40 g mol −1 Mass of octane, w 1 = 114 g Molar mass of octane, (C 8 H 18 ), M 1 = 8 × 12 + 18 × 1 = 114 g mol −1 Applying the relation, 
Hence, the required mass of the solute is 8 g.
And, the no. of moles of solute, 
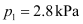Applying the relation: 
After the addition of 18 g of water: 
Again, applying the relation: 
Dividing equation (i) by (ii), we have: 
Therefore, the molar mass of the solute is 23 g mol −1. (ii) Putting the value of ‘M’ in equation (i), we have: .gif)
Hence, the vapour pressure of water at 298 K is 3.53 kPa. Page No 60:
= 0.0146 mol Therefore, molality of the solution, 
= 0.1537 mol kg −1 Applying the relation, ΔT f = K f × m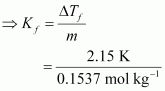 
= 13.99 K kg mol −1 Molar of glucose (C 6 H 12 O 6 ) = 6 × 12 + 12 × 1 + 6 × 16 = 180 g mol −1 5% glucose in water means 5 g of glucose is present in (100 − 5) g = 95 g of water. ∴ Number of moles of glucose 
= 0.0278 mol Therefore, molality of the solution, 
= 0.2926 mol kg −1 Applying the relation, ΔT f = K f × m = 13.99 K kg mol −1 × 0.2926 mol kg−1 = 4.09 K (approximately) Hence, the freezing point of 5% glucose solution is (273.15 − 4.09) K= 269.06 K.
Then, 
= 110.87 g mol −1 
= 196.15 g mol −1 Now, we have the molar masses of AB 2 and AB 4 as 110.87 g mol −1 and 196.15 g mol−1 respectively. Let the atomic masses of A and B be x and y respectively. Now, we can write: 
Subtracting equation (i) from (ii), we have 2y = 85.28 ⇒ y = 42.64 Putting the value of ‘y’ in equation (1), we have x + 2 × 42.64 = 110.87 ⇒ x = 25.59 Hence, the atomic masses of A and B are 25.59 u and 42.64 u respectively. Question 33. At 300 K, 36 g of glucose present in a litre of its solution has an osmotic pressure of 4.98 bar. If the osmotic pressure of the solution is 1.52 bars at the same temperature, what would be its concentration? 
= 0.061 mol Since the volume of the solution is 1 L, the concentration of the solution would be 0.061 M.
has polar −OH group and can form H−bond. Thus, it is highly soluble in water. (v) Chloroform is insoluble in water. (vi) Pentanol (C 5 H 11 OH) has polar −OH group, but it also contains a very bulky non-polar −C 5 H 11 group. Thus, pentanol is partially soluble in water.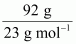
= 4 mol Therefore, molality of Na + ions in the lake 
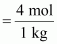= 4 m
Now, 
= s × s = s 2 Then, we have, K sp = 
= 2.45 × 10 −8 mol L−1 Hence, the maximum molarity of CuS in an aqueous solution is 2.45 × 10 −8 mol L −1. 
= 1.424% Question 40. Nalorphene (C 19 H 21 NO 3 ), similar to morphine, is used to combat withdrawal symptoms in narcotic users. Dose of nalorphene generally given is 1.5 mg. Calculate the mass of 1.5 × 10 −3 m aqueous solution required for the above dose. 
is given as: 
In 1.5 × 10 −3 m aqueous solution of nalorphene, 1 kg (1000 g) of water contains 1.5 × 10 −3 mol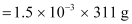 
= 0.4665 g Therefore, total mass of the solution 
This implies that the mass of the solution containing 0.4665 g of nalorphene is 1000.4665 g. Therefore, mass of the solution containing 1.5 mg of nalorphene is: 
Hence, the mass of aqueous solution required is 3.22 g.
mol of benzoic acid = 0.0375 mol of benzoic acid Molar mass of benzoic acid (C 6 H 5 COOH) = 7 × 12 + 6 × 1 + 2 × 16 = 122 g mol −1 Hence, required benzoic acid = 0.0375 mol × 122 g mol −1 = 4.575 g Question 42. The depression in freezing point of water observed for the same amount of acetic acid, trichloroacetic acid and trifluoroacetic acid increases in the order given above. Explain briefly. 
Among H, Cl, and F, H is least electronegative while F is most electronegative. Then, F can withdraw electrons towards itself more than Cl and H. Thus, trifluoroacetic acid can easily lose H + ions i.e., trifluoroacetic acid ionizes to the largest extent. Now, the more ions produced, the greater is the depression of the freezing point. Hence, the depression in the freezing point increases in the order: Acetic acid < trichloroacetic acid < trifluoroacetic acid
∴No. of moles present in 10 g of 
= 0.0816 mol It is given that 10 g of 
is added to 250 g of water. ∴Molality of the solution, 
Let α be the degree of dissociation of 
undergoes dissociation according to the following equation: 
Since α is very small with respect to 1, 1 − α ≈ 1 Now, 
Again, 
Total moles of equilibrium = 1 − α + α + α = 1 + α 
Hence, the depression in the freezing point of water is given as: 
Question 44. 19.5 g of CH 2 FCOOH is dissolved in 500 g of water. The depression in the freezing point of water observed is 1.0°C. Calculate the van’t Hoff factor and dissociation constant of fluoroacetic acid. Solution : It is given that: 
We know that: 
Therefore, observed molar mass of 
The calculated molar mass of 
is: 
Therefore, van’t Hoff factor, 
Let α be the degree of dissociation of 
Now, the value of K a is given as: 
Taking the volume of the solution as 500 mL, we have the concentration: 
Therefore, 
= 17.535 mm of Hg Mass of glucose, w 2 = 25 g Mass of water, w 1 = 450 g We know that, Molar mass of glucose (C 6 H 12 O 6 ), M 2 = 6 × 12 + 12 × 1 + 6 × 16 = 180 g mol −1 Molar mass of water, M 1 = 18 g mol −1 Then, number of moles of glucose, 
= 0.139 mol And, number of moles of water, 
= 25 mol We know that, 
⇒ 17.535 − p 1 = 0.097 ⇒ p 1 = 17.44 mm of Hg Hence, the vapour pressure of water is 17.44 mm of Hg. Question 46. Henry’s law constant for the molality of methane in benzene at 298 Kis 4.27 × 10 5 mm Hg. Calculate the solubility of methane in benzene at 298 Kunder 760 mm Hg. 
= 177.99 × 10 −5 = 178 × 10 −5 (approximately) Hence, the mole fraction of methane in benzene is 178 × 10 −5. 
= 0.714 mol Number of moles of liquid B, 
= 5.556 mol Then, mole fraction of A, 
= 0.114 And, mole fraction of B, x B = 1 − 0.114 = 0.886 Vapour pressure of pure liquid B, 
= 500 torr Therefore, vapour pressure of liquid B in the solution, 
= 500 × 0.886 = 443 torr Total vapour pressure of the solution, p total = 475 torr ∵ Vapour pressure of liquid A in the solution, p A = p total − p B = 475 − 443 = 32 torr Now, 
= 280.7 torr Hence, the vapour pressure of pure liquid A is 280.7 torr.| 100 ×x acetone | 0 | 11.8 | 23.4 | 36.0 | 50.8 | 58.2 | 64.5 | 72.1 |
| p acetone /mm Hg | 0 | 54.9 | 110.1 | 202.4 | 322.7 | 405.9 | 454.1 | 521.1 |
| p chloroform /mm Hg | 632.8 | 548.1 | 469.4 | 359.7 | 257.7 | 193.6 | 161.2 | 120.7 |
| 100 ×x acetone | 0 | 11.8 | 23.4 | 36.0 | 50.8 | 58.2 | 64.5 | 72.1 |
| p acetone /mm Hg | 0 | 54.9 | 110.1 | 202.4 | 322.7 | 405.9 | 454.1 | 521.1 |
| p chloroform /mm Hg | 632.8 | 548.1 | 469.4 | 359.7 | 257.7 | 193.6 | 161.2 | 120.7 |
| p tota (mm Hg) | 632.8 | 603.0 | 579.5 | 562.1 | 580.4 | 599.5 | 615.3 | 641.8 |
It can be observed from the graph that the plot for the p total of the solution curves downwards. Therefore, the solution shows negative deviation from the ideal behaviour.
Molar mass of toluene 
Now, no. of moles present in 80 g of benzene 
= 1.026 And, no. of moles present in 100 g of toluene = 100/92 = 1.087 mol ∴Mole fraction of benzene, x b 
And, mole fraction of toluene, 
It is given that vapour pressure of pure benzene, 
And, vapour pressure of pure toluene, 
Therefore, partial vapour pressure of benzene,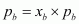 
And, partial vapour pressure of toluene, 
Hence, mole fraction of benzene in vapour phase is given by: 
Question 50. The air is a mixture of a number of gases. The major components are oxygen and nitrogen with approximate proportion of 20% is to 79% by volume at 298 K. The water is in equilibrium with air at a pressure of 10 atm. At 298 Kif the Henry’s law constants for oxygen and nitrogen are 3.30 × 10 7 mm and 6.51 × 10 7 mm respectively, calculate the composition of these gases in water.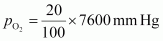 
= 1520 mm Hg Partial pressure of nitrogen, 
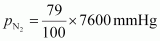= 6004 mmHg Now, according to Henry’s law: p = K H .x For oxygen: 
For nitrogen: 
Hence, the mole fractions of oxygen and nitrogen in water are 4.61 ×10 −5and 9.22 × 10−5 respectively. Question 51. Determine the amount of CaCl 2 (i = 2.47) dissolved in 2.5 litre of water such that its osmotic pressure is 0.75 atm at 27°C. Solution : We know that, 
Here, R = 0.0821 L atm K -1mol-1 M = 1 × 40 + 2 × 35.5 = 111g mol -1 Therefore, w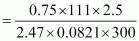 
= 3.42 g Hence, the required amount of CaCl 2 is 3.42 g.
ions are produced. ⇒ Total number of ions produced = 3 ⇒ i =3 Given, w = 25 mg = 0.025 g V = 2 L T = 25 0C = (25 + 273) K = 298 K Also, we know that: R = 0.0821 L atm K -1mol-1 M = (2 × 39) + (1 × 32) + (4 × 16) = 174 g mol -1 Appling the following relation, 
NCERT Solutions for Class 12 Chemistry Chapter 2 Solutions FAQs
Which chapter of chemistry class 12 is most important?
Organic chemistry is the most important topic for CBSE Class 12 Chemistry exam.
What is the important reaction in aldehyde ketone and carboxylic acid?
The carbonyl groups in aldehydes and ketones can be oxidized to form the next “oxidation level” compound-carboxylic acid. Adding water to an aldehyde or ketone produces a product called a hydrate or gemdiol (two OH groups on one carbon). The reaction is catalyzed by acids and bases.
Is Class 12 chemistry difficult?
“As per my meticulous observation, the difficulty level of the Chemistry paper of Class 12 was high. The questions asked in the paper were tricky, although they were from the NCERT course.
What are the 4 main elements of organic chemistry?
Four elements, hydrogen, carbon, oxygen and nitrogen, are the major components of most organic compounds.
Is ketone acidic or basic?
The acidosis is usually attributed to the 'acidic' nature of the ketone bodies (acetoacetate, 3-hydroxybutyrate, and acetone). However, acetoacetate and 3-hydroxybutyrate are produced not as acids but as their conjugate bases, and acetone is neither an acid nor a base.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App