NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise
NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise contains all the questions with detailed solutions. Students are advised to solve these questions for better understanding of the concepts.
Krati Saraswat30 Jan, 2024
Share
NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise
NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise Applications of Derivatives is prepared by the academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of Chapter 6. Given below is step by step solutions of all questions given in the NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise.NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise Overview
NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise is prepared by our experts to help students understand the concepts of the chapter better. Students can solve these questions before their examinations these questions will help them to understand the concepts better and by doing these questions students can easily ace their examinations.NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise
Solve The Following Questions NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise
Question 1. Using differentials, find the approximate value of each of the following: (a) (17/81) 1/4 (b) (33) 1/5 Solution :
= 0.497
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.1
Question 2. Show that the function given by f(x) = logx / x has maximum value at x = e Solution :
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2
Question 3. The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base? Solution : Let ΔABC be isosceles where BC is the base of fixed length b . Let the length of the two equal sides of ΔABC be a . Draw AD⊥BC.
Therefore, the area is decreasing at the rate of √3b cm
2
/s.
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.3
Question 4. Find the equation of the normal to the curve y 2 = 4 x at the point (1, 2). Solution : Equation of the curve is y 2 = 4 x ……….(i)
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.4
Question 5. Show that the normal at any point θ to the curve x = a cosθ + a θ sin θ, y = a sin θ - aθ cos θ is at a constant distance from the origin. Solution : We have x = a cos θ + a θ sin θ .
Hence, the perpendicular distance of the normal from the origin is constant.
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5
Question 6. Find the intervals in which the function f given by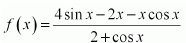
is (i) increasing (ii) decreasing.
Solution :
Question
7. Find the intervals in which the function f given by
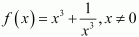is (i) increasing (ii) decreasing.
Solution :
Question
8. Find the maximum area of an isosceles triangle inscribed in the ellipse
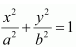with its vertex at one end of the major axis.
Solution :
Equation of the ellipse is
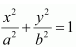
Let the major axis be along the
x
−axis.
Let ABC be the triangle inscribed in the ellipse where vertex C is at (
a
, 0).
Since the ellipse is symmetrical with respect to the
x
−axis and
y
−axis, we can assume the coordinates of A to be (−
x
1
,
y
1
) and the coordinates of B to be (−
x
1
, −
y
1
).
Question 9. A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m3. If building of tank costs ` 70 per sq. meter for the base and ` 45 per square meter for sides. What is the cost of least expensive tank?
Solution :
Given: Depth of tank = 2 m
Let
l
,
b
, and
h
represent the length, breadth, and height of the tank respectively.
Then, we have height (
h)
= 2 m
Volume of the tank = 8m
3
Volume of the tank =
l
×
b
×
h
∴ 8 =
l
×
b
× 2
lb = 4, b = 4/l
Now, area of the base =
lb
= 4
Area of the 4 walls (
A)
= 2
h
(
l
+
b)
Thus, by second derivative test, the area is the minimum when
l
= 2.
We have
l
=
b
=
h
= 2.
∴Cost of building the base = Rs 70 × (
lb
) = Rs 70 (4) = Rs 280
Cost of building the walls = Rs 2
h
(
l
+
b
) × 45 = Rs 90 (2) (2 + 2)
= Rs 8 (90) = Rs 720
Required total cost = Rs (280 + 720) = Rs 1000
Hence, the total cost of the tank will be Rs 1000.
Question
10. The sum of the perimeter of a circle and square is k where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
Solution :
Let r be the radius of the circle and a be the side of square.
Therefore, sum of areas is minimum when side of the square is double the radius of the circle.
Question
11. A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening.
Solution :
Let
x
and
y
be the length and breadth of the rectangular window.
Radius of the semicircular opening = x/2
It is given that the perimeter of the window is 10 m.
∴Area of the window (
A)
is given by,
Thus, when
Therefore, by second derivative test, the area is the maximum when length x = 20/π + 4m.
Hence, the required dimensions of the window to admit maximum light is given bylength = 20/π+4m and breadth = 10/π+4m.
Question
12. A point on the hypotenuse of a triangle is at distances a and b from the sides of the triangle. Show that the maximum length of the hypotenuse is
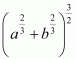Solution :
Let ΔABC be right-angled at B. Let AB =
x
and BC =
y
.
Let P be a point on the hypotenuse of the triangle such that P is at a distance of
a
and
b
from the sides AB and BC respectively.
Let ∠C =
θ
.
We have,
AC = √x
2
+ y
2
Now,
PC =
b
cosec
θ
And, AP =
a
sec
θ
∴AC = AP + PC
⇒ AC =
b
cosec
θ
+
a
sec
θ
… (1)
Therefore, by second derivative test, the length of the hypotenuse is the maximum when tan θ(b/a)
1/3
Now, when tan θ(b/a)
1/3
, we have:
Hence, the maximum length of the hypotenuses is
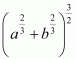Question
13. Find the points at which the function f given by f(x) = (x - 2)
4
(x + 1)
3
has:
(i) local maxima
(ii) local minima
(iii) point of inflexion.
Solution :
Given: f(x) = (x - 2)
4
(x + 1)
3
Now, for values of
x
close to 2/7 and to the left of 2/7, f'(x) > 0. Also, for values of
x
close to 2/7 and to the right of 2/7, f'(x) < 0
Thus, x = 2/7 is the point of local maxima.
Now, for values of
x
close to 2 and to the left of 2, f'(x) < 0 Also, for values of
x
close to 2 and to the right of 2, f'(x) > 0
Thus,
x
= 2 is the point of local minima.
Now, as the value of
x
varies through −1,f'(x) does not changes its sign.
Thus,
x
= −1 is the point of inflexion.
Question
14. Find the absolute maximum and minimum values of the function f given by f(x) = cos
2
x + sin x , x ∊ [0,π ]
Solution :
Given:f(x) = cos
2
x + sin x ……….(i)
Now, evaluating the value of
f
at critical points x = π/2 and x = π/6 and at the end points of the interval [0,π ] (i.e., at
x
= 0 and
x
= π), we have:
Hence, the absolute maximum value of
f
is 5/4 occurring at x = π/6 and the absolute minimum value of
f
is 1 occurring at x = 0, π/2, and π.
Question
15. Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is 4r/3
Solution :
Let r be the radius of base of cone and h be the height of the cone inscribed in a sphere of radius
The volume (
V)
of the cone is given by,
V = 1/3πR
2
h
Now, from the right triangle BCD, we have:
BC = √r
2
- R
2
∴
h
= r+√r
2
- R
2
Hence, it can be seen that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius
r
is 4r/3.
Question
16. Let
f
be a function defined on [
a
,
b
] such that
f
'(
x
) > 0, for all
x
∈ (
a
,
b
). Then prove that
f
is an increasing function on (
a
,
b
).
Solution :
Let x1, x2∈(a,b) such that x1<x2.
Consider the sub-interval [x1, x2]. Since f(x) is differentiable on (a, b) and [x1, x2]⊂(a,b).
Therefore, f(x) is continous on [x1, x2] and differentiable on (x1, x2).
By the Lagrange's mean value theorm, there exists c∈(x1, x2) such that
f'(c)=f(x2)-f(x1)x2-x1 ...(1)
Since f'(x) ) > 0 for all x∈(a,b), so in particular, f'(c) > 0.
f'(c)>0⇒f(x2)-f(x1)x2-x1>0 [Using (1)]
⇒f(x2)-f(x1)>0 [∵ x2-x1>0 when x1<x2]
⇒f(x2)>f(x1)⇒f(x1)<f(x2)
Since x1, x2 are arbitrary points in (a,b).
Therefore, x1<x2⇒f(x1)<f(x2) for all x1,x2∈(a, b)
Hence,f(x) is increasing on (a,b).
Question
17. Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R/√3 Also find the maximum volume.
Solution :
A sphere of fixed radius (
R)
is given.
Let
r
and
h
be the radius and the height of the cylinder respectively.
From the given figure, we have h = 2√R
2
- r
2
The volume (
V)
of the cylinder is given by,
Now, it can be observed that at
∴The volume is the maximum when r
2
= 2R
2
/3
When r
2
= 2R
2
/3, the height of the cylinder is
Hence, the volume of the cylinder is the maximum when the height of the cylinder is
2R/√3
Question
18. Show that the height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and having semi-vertical angle
α
is one-third that of the cone and the greatest volume of the cylinder is 4/27πh
3
tan2
α
.
Solution :
The given right circular cone of fixed height (
h)
and semi-vertical angle (
α
)
can be drawn as:
Here, a cylinder of radius
R
and height
H
is inscribed in the cone.
Then, ∠GAO =
α
, OG =
r
, OA =
h
, OE =
R
, and CE =
H
.
We have,
r
=
h
tan
α
Now, since ΔAOG is similar to ΔCEG, we have:
Now, the volume (
V)
of the cylinder is given by,
∴By second derivative test, the volume of the cylinder is the greatest when
Thus, the height of the cylinder is one-third the height of the cone when the volume of the cylinder is the greatest.
Now, the maximum volume of the cylinder can be obtained as:
Choose the correct answer in the Exercises 19 to 24:
Question
19. A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic meter per hour. Then the depth of wheat is increasing at the rate of:
(A) 1 m/h
(B) 0.1 m/h
(C) 1.1 m/h
(D) 0.5 m/h
Solution :
Let
r
be the radius of the cylinder.
Then, volume (
V)
of the cylinder is given by,
Differentiating with respect to time
t
, we have:
The tank is being filled with wheat at the rate of 314 cubic metres per hour.
Thus, we have:
Hence, the depth of wheat is increasing at the rate of 1 m/h.
The correct answer is A.
Question
20. The slope of the tangent to the curve x = t
2
+ 3t – 8, y = 2t
2
– 2t – 5 at the point (2,– 1) is
(A) 22/7
(B) 6/7
(C) 7/6
(D) -6/7
Solution :
The given curve is x = t
2
+ 3t – 8 and y = 2t
2
– 2t – 5
The given point is (2, −1).
At
x
= 2, we have:
The common value of
t
is 2.
Hence, the slope of the tangent to the given curve at point (2, −1) is
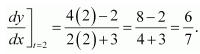Therefore, option (B) is correct.
Question
21.
The line
y
=
mx
+ 1 is a tangent to the curve
y
2
= 4
x
if the value of
m
is
(A) 1
(B) 2
(C) 3
(D) 1/2
Solution :
The equation of the tangent to the given curve is
y
=
mx
+ 1.
Now, substituting
y
=
mx
+ 1 in
y
2
= 4
x
, we get:
Since a tangent touches the curve at one point, the roots of equation (i) must be equal.
Therefore, we have:
Discriminant = 0
Hence, the required value of
m
is 1.
Therefore, option (A) is correct.
Question
22.
The normal at the point (1, 1) on the curve 2
y
+
x
2
= 3 is
(A) x + y = 0
(B) x − y = 0
(C) x + y + 1 = 0
(D) x − y = 1
Solution : The equation of the given curve is 2 y + x 2 = 3. Differentiating with respect to x , we have:
The slope of the normal to the given curve at point (1, 1) is
Hence, the equation of the normal to the given curve at (1, 1) is given as:
⇒ y - 1 = 1(x - 1)
⇒ y - 1 = x - 1
⇒ x - y = 0
Therefore, option (B) is correct.
Question
23.
The normal to the curve
x
2
= 4
y
passing (1, 2) is
(A) x + y = 3
(B) x − y = 3
(C) x + y = 1
(D) x − y = 1
Solution : The equation of the given curve is x 2 = 4 y . Differentiating with respect to x , we have:
The slope of the normal to the given curve at point (
h
,
k
) is given by,
∴Equation of the normal at point (
h
,
k
) is given as:
Now, it is given that the normal passes through the point (1, 2).
Therefore, we have:
Since (
h
,
k
) lies on the curve
x
2
= 4
y
, we have
h
2
= 4
k.
⇒ k =h
2
/4
From equation (i), we have:
Hence, the equation of the normal is given as:
Therefore, option (A) is correct.
Question
24. The points on the curve 9
y
2
=
x
3
where the normal to the curve make equal intercepts with axes are:
Solution :
The equation of the given curve is 9
y
2
=
x
3
.
Differentiating with respect to
x
, we have:
The slope of the normal to the given curve at point (x
1
,y
1
) is
∴ The equation of the normal to the curve at (x
1
,y
1
) is
It is given that the normal makes equal intercepts with the axes.
Therefore, We have:
Also, the point(x
1
,y
1
)lies on the curve, so we have
9y
1
2
= x
1
3
.....................(ii)
From (i) and (ii), we have:
Therefore, option (A) is correct.
NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise FAQs
Are miscellaneous questions important for class 12 maths?
Miscellaneous questions are very important and meaningful. It is advised to practice miscellaneous exercises which are available at the end of the chapters in NCERT books.
Is miscellaneous exercise important for class 12 board 2024?
This exercise is considered to be tough as compared to the previous exercises but it is not as important as previous exercises of this chapter for board exams. There are very few questions in board exams that are asked from miscellaneous exercises but it is very important for competitive exams.
How many exercises are there in Chapter 6 Maths Class 12?
Class 12 Maths Chapter 6 Application of Derivatives has 102 questions in 6 exercises along with 24 more provided in a miscellaneous exercise.
Which chapter is required for application of derivatives?
In chapter 6, we are going to learn how to determine the rate of change of quantity, finding the equations of tangents, finding turning points on the graphs for various functions, maxima and minima and so on.
Why do we use derivatives in math?
Derivatives are used to find the rate of changes of a quantity with respect to the other quantity.
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.