NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5 (Applications of Derivatives)
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5 contains all the questions with detailed solutions. Students are advised to solve these questions for better understanding of the concepts in exercise 6.5.
Krati Saraswat2 Feb, 2024
Share
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5 (Applications of Derivatives)
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5 Applications of Derivatives is prepared by the academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of Chapter 6. Given below is step by step solutions of all questions given in NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5.NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5 Overview
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5 covers these important topics. Students are encouraged to review each topic thoroughly in order to fully understand the concepts taught in the chapter and make optimal use of the provided solutions. These solutions are the outcome of the dedicated effort that the Physics Wallah teachers have been doing to aid students in understanding the ideas covered in this chapter. After going over and rehearsing these responses, the goal is for students to easily score outstanding exam results.NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5
Solve The Following Questions of NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5:
NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise
Question 1. Find the maximum and minimum values, if any, of the following functions given by (i) f(x) = (2x − 1) 2 + 3 (ii) f(x) = 9x 2 + 12x + 2 (iii) f(x) = −(x − 1) 2 + 10 (iv) g(x) =x 3 + 1 Solution : (i) The given function is f(x) = (2x − 1) 2 + 3. It can be observed that (2x− 1) 2 ≥ 0 for every x∈R. Therefore, f(x) = (2x − 1) 2 + 3 ≥ 3 for every x∈R. The minimum value of f is attained when 2x − 1 = 0. 2x − 1 = 0⇒ x = 1/2 ∴Minimum value of f =
= 3
Hence, functionf does not have a maximum value.
(ii) The given function is f(x) = 9x
2
+ 12x + 2 = (3x + 2)
2
− 2.
It can be observed that (3x + 2)
2
≥ 0 for every x∈R.
Therefore, f(x) = (3x + 2)
2
− 2 ≥ −2 for every x∈R.
The minimum value of f is attained when 3x + 2 = 0.
3x + 2 = 0⇒ x = -2/3
∴Minimum value off =
Hence, functionf does not have a maximum value.
(iii) The given function is f(x) = − (x − 1)
2
+ 10.
It can be observed that (x − 1)
2
≥ 0 for every x∈R.
Therefore,f(x) = − (x − 1)2 + 10 ≤ 10 for every x∈R.
The maximum value off is attained when (x − 1) = 0.
(x − 1) = 0⇒x = 1
∴Maximum value off = f(1) = − (1 − 1)
2
+ 10 = 10
Hence, functionf does not have a minimum value.
(iv) The given function isg(x) =x
3
+ 1.
Hence, functiong neither has a maximum value nor a minimum value.
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.1
Question 2. Find the maximum and minimum values, if any, of the following functions given by (i) f(x) = |x + 2| − 1 (ii) g(x) = − |x + 1| + 3 (iii) h(x) = sin(2x) + 5 (iv) f(x) = |sin 4x + 3| (v) h(x) =x+ 1,x ∈ (−1, 1) Solution :
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.1
Question 3. Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be: (i).f(x) =x 2 (ii).g(x) =x 3 − 3x (iii) h(x) = sinx + cosx, 0 < x < π/2 (iv) f(x) = sinx − cosx, 0 <x < 2π (v) f(x) =x 3 − 6x 2 + 9x + 15 (v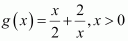i)
(vii)
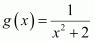(viii)
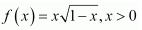Solution :
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2
Question 4. Prove that the following functions do not have maxima or minima: (i) f(x) =ex (ii) g(x) = logx (iii) h(x) =x 3 +x 2 + x + 1 Solution : We have, f(x) = ex ∴ f'(x) = e x Now, if f'(x) = 0. But, the exponential function can never assume 0 for any value ofx. Therefore, there does not existc∈R such that f'(c) = 0 Hence, functionf does not have maxima or minima. We have, g(x) = logx ∴ g'(x) = 1/x Since log xnis defined for a positive number x, g'(x) > 0 for any x Therefore, there does not existc∈R such that g'(c) = 0 Hence, functiong does not have maxima or minima. We have, h(x) =x 3 +x 2 +x + 1 h'(x) =3x 2 +2x + 1 Now, h(x) = 0 ⇒ 3x 2 + 2x + 1 = 0⇒
Therefore, there does not exist c∈R such that h'(c) = 0
Hence, functionh does not have maxima or minima.
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.3
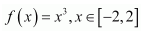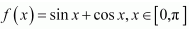Question 5. Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals: (i)
(ii)
(iii)
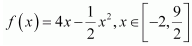(iv)
Solution :
(i) The given function isf(x) = x3.
f'(x) = 3x
2
Now, f'(x) = 0 ⇒ x = 0
Then, we evaluate the value off at critical point x = 0 and at end points of the interval [−2, 2].
f(0) = 0
f(−2) = (−2)
3
= −8
f(2) = (2)
3
= 8
Hence, we can conclude that the absolute maximum value off on [−2, 2] is 8 occurring atx = 2. Also, the absolute minimum value off on [−2, 2] is −8 occurring at x = −2.
(ii) The given function is f(x) = sinx + cosx.
Then, we evaluate the value off at critical point π/4 and at the end points of the interval [0, π].
Hence, we can conclude that the absolute maximum value off on [0, π] is√2 occurring atx = π4 and the absolute minimum value off on [0, π] is −1 occurring atx = π.
Then, we evaluate the value off at critical pointx = 4 and at the end points of the interval
.
Hence, we can conclude that the absolute maximum value off on
is 8 occurring atx = 4 and the absolute minimum value off on
is −10 occurring atx = −2.
Hence, we can conclude that the absolute maximum value off on [−3, 1] is 19 occurring atx = −3 and the minimum value off on [−3, 1] is 3 occurring atx = 1.
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.4
Question 6. Find the maximum profit that a company can make, if the profit function is given by p(x) = 41 − 72x − 18x 2 Solution : The profit function is given as p (x) = 41 − 72x− 18x 2 . ∴ p'(x)=−72−36x ⇒ x=−7236 =−2 Also, p''(−2)=−36 <0 By second derivative test, x=−2 is the point of local maxima of p. ∴ Maximum profit=p(−2) =41−72(−2)−18(−2) 2 =41+144−72=113 Hence, the maximum profit that the company can make is 113 units. The solution given in the book has some error. The solution is created according to the question given in the book. Question 7. Find both the maximum value and the minimum value of 3x 4 − 8x 3 + 12x 2 − 48x + 25 on the interval [0, 3] Solution : Let f(x) = 3x 4 − 8x 3 + 12x 2 − 48x + 25.
Now,f'(x) = 0 gives x = 2 or x
2
+ 2 = 0 for which there are no real roots.
Therefore, we consider only x = 2∈[0, 3].
Now, we evaluate the value off at critical pointx = 2 and at the end points of the interval [0, 3].
Hence, we can conclude that the absolute maximum value offon [0, 3] is 25 occurring atx= 0 and the absolute minimum value off at [0, 3] is − 39 occurring atx = 2.
Question
8. At what points in the interval [0, 2π], does the function sin 2x attain its maximum value?
Solution :
Letf(x) = sin 2x.
Question
9. What is the maximum value of the function sinx + cosx?
Solution :
Let f(x) = sinx + cosx.
Now,f''(x) will be negative when (sinx + cosx) is positive i.e., when sin xand cosxare both positive. Also, we know that sinx and cosx both are positive in the first quadrant. Then,f''(x) will be negative when x ∊ (0, π/2).
Thus, we consider x = π/4
∴By second derivative test,f will be the maximum at x = π/4 and the maximum value of f is
.
Question
10. Find the maximum value of 2x
3
− 24x + 107 in the interval [1, 3]. Find the maximum value of the same function in [−3, −1].
Solution :
Let f(x) = 2x
3
− 24x + 107.
We first consider the interval [1, 3].
Then, we evaluate the value off at the critical pointx = 2∈ [1, 3] and at the end points of the interval [1, 3].
f(2) = 2(8) − 24(2) + 107 = 16 − 48 + 107 = 75
f(1) = 2(1) − 24(1) + 107 = 2 − 24 + 107 = 85
f(3) = 2(27) − 24(3) + 107 = 54 − 72 + 107 = 89
Hence, the absolute maximum value off(x) in the interval [1, 3] is 89 occurring atx = 3.
Next, we consider the interval [−3, −1].
Evaluate the value off at the critical pointx = −2∈ [−3, −1] and at the end points of the interval [1, 3].
f(−3) = 2 (−27) − 24(−3) + 107 = −54 + 72 + 107 = 125
f(−1) = 2(−1) − 24 (−1) + 107 = −2 + 24 + 107 = 129
f(−2) = 2(−8) − 24 (−2) + 107 = −16 + 48 + 107 = 139
Hence, the absolute maximum value off(x) in the interval [−3, −1] is 139 occurring atx = −2.
Question
11. It is given that atx = 1, the function x
4
− 62x
2
+ax + 9 attains its maximum value, on the interval [0, 2]. Find the value of a.
Solution :
Let f(x) =x
4
− 62x
2
+ax + 9.
Hence, the value ofa is 120.
Question
12. Find the maximum and minimum values ofx + sin 2x on [0, 2π].
Solution :
Let f(x) =x + sin 2x.
Hence, we can conclude that the absolute maximum value off(x) in the interval [0, 2π] is 2π occurring atx = 2π and the absolute minimum value off(x) in the interval [0, 2π] is 0 occurring atx = 0.
Question
13. Find two numbers whose sum is 24 and whose product is as large as possible.
Solution :
Let one number be x. Then, the other number is (24 −x).
Let P(x) denote the product of the two numbers. Thus, we have:
∴By second derivative test,x = 12 is the point of local maxima of P. Hence, the product of the numbers is the maximum when the numbers are 12 and 24 − 12 = 12.
Question
14. Find two positive numbers x andy such that x +y = 60 and xy
3
is maximum.
Solution :
The two numbers arex andy such that x +y = 60.
⇒y = 60 −x
Let f(x) =xy
3
.
∴By second derivative test,x= 15 is a point of local maxima off. Thus, functionxy3 is maximum whenx = 15 andy = 60 − 15 = 45.
Hence, the required numbers are 15 and 45.
Question
15. Find two positive numbersxandysuch that their sum is 35 and the product x
2
y
5
is a maximum
Solution :
Let one number bex. Then, the other number is y = (35 −x).
Let P(x) =x
2
y
5
. Then, we have:
∴ By second derivative test,
P
(
x
) will be the maximum when
x
= 10 and
y
= 35 − 10 = 25.
Hence, the required numbers are 10 and 25.
Question
16. Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.
Solution :
Let one number be x. Then, the other number is (16 −x).
Let the sum of the cubes of these numbers be denoted by S(x). Then,
∴ By second derivative test, x = 8 is the point of local minima of S.
Hence, the sum of the cubes of the numbers is the minimum when the numbers are 8 and 16 − 8 = 8.
Question
17. A square piece of tin of side 18 cm is to made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
Solution :
Let the side of the square to be cut off be x cm. Then, the length and the breadth of the box will be (18 − 2x) cm each and the height of the box is x cm.
Therefore, the volume V(x) of the box is given by,
∴ By second derivative test,x = 3 is the point of maxima of V.
Hence, if we remove a square of side 3 cm from each corner of the square tin and make a box from the remaining sheet, then the volume of the box obtained is the largest possible.
Question
18. A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
Solution :
Let the side of the square to be cut off be x cm. Then, the height of the box isx, the length is 45 − 2x, and the breadth is 24 − 2x.
Therefore, the volumeV(x) of the box is given by,
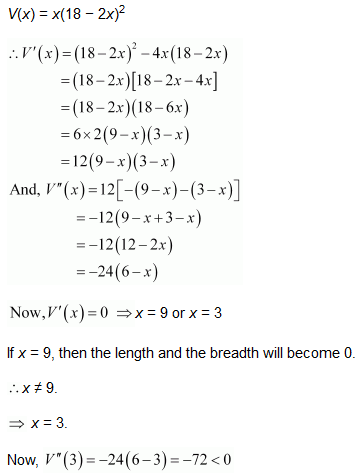∴By second derivative test,x = 5 is the point of maxima.
Hence, the side of the square to be cut off to make the volume of the box maximum possible is 5 cm.
Question
19. Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
Solution :
Let a rectangle of lengthl and breadthb be inscribed in the given circle of radiusa.
Then, the diagonal passes through the centre and is of length 2a cm.
∴By the second derivative test, when l = √2a , then the area of the rectangle is the maximum.
Since l = b = √2a, the rectangle is a square.
Hence, it has been proved that of all the rectangles inscribed in the given fixed circle, the square has the maximum area.
Question
20. Show that the right circular cylinder of given surface and maximum volume is such that is heights is equal to the diameter of the base.
Solution :
Letr andh be the radius and height of the cylinder respectively.
Then, the surface area (S) of the cylinder is given by,
Hence, the volume is the maximum when the height is twice the radius i.e., when the height is equal to the diameter.
Question
21. Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area?
Solution :
Letr andh be the radius and height of the cylinder respectively.
Then, volume (V) of the cylinder is given by,
Question
22. A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
Solution :
Let a piece of lengthl be cut from the given wire to make a square.
Then, the other piece of wire to be made into a circle is of length (28 −l) m.
Now, side of square = l/4
Letr be the radius of the circle. Then, 2πr = 28 -
l
⇒ r = 1/2π(28 - l)
The combined areas of the square and the circle (A) is given by,
Question
23. Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is 8/27 of the volume of the sphere.
Solution :
Letr andh be the radius and height of the cone respectively inscribed in a sphere of radius R.
Question
24. Show that the right circular cone of least curved surface and given volume has an altitude equal to √2 time the radius of the base.
Solution :
Let randh be the radius and the height (altitude) of the cone respectively.
Then, the volume (V) of the cone is given as: V =13πr
2
h ⇒ h =3Vπr
2
The surface area (S)of the cone is given by,
S = πrl (wherel is the slant height)
Hence, for a given volume, the right circular cone of the least curved surface has an altitude equal to√2 times the radius of the base.
Question
25. Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is tan
-1
√2
Solution :
Letθ be the semi-vertical angle of the cone.
It is clear that
Let r,h, and l be the radius, height, and the slant height of the cone respectively.
The slant height of the cone is given as constant.
Now,r =l sinθ and h =l cosθ
The volume (V) of the cone is given by,
V=1/3πr
2
h =1/3π (l
2
sin
2
θ)(lcosθ)
=1/3πl
3
sinθ cosθ
⇒dV/dθ =l
3
π/3 [sin
2
θ (−sinθ) + cosθ(2sinθ cosθ)]
=l
3
π / 3[−sin3θ+2sinθcos2θ]
⇒d
2
V / dθ
2
=l
3
π / 3 [−3sin
2
θ cosθ + 2cos
3
θ− 4sin
2
θ cosθ ]
=l3π/3 [2cos
3
θ − 7sin
2
θ cosθ]
∴By second derivative test, the volume (V) is the maximum when
θ = tan
-1
√2
Hence, for a given slant height, the semi-vertical angle of the cone of the maximum volume is
tan
-1
√2.
Question
26. Show that semi-vertical angle of right circular cone of given surface area and maximum volume is
sin
-1
(1/3)
Solution :
Let r be the radius, l be the slant height and h be the height of the cone of given surface area,S.
Also, let α be the semi-vertical angle of the cone.
Question
27. The point on the curve x
2
= 2y which is nearest to the point (0, 5) is
(A) (2√2 , 4)
(B) (2√2 , 0)
(C) (0, 0)
(D) (2, 2)
Solution :
Equation of the curve is x
2
= 2y
For each value of
x
, the position of the point will be(x, x
2
/2)
Let P (x, x
2
/2) be any point on the curve (i), then according to question,
Distance between given point (0, 5) and
Therefore, option (A) is correct.
Question
28. For all real values of x, the minimum value of
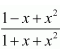is
(A) 0
(B) 1
(C) 3
(D) 1/3
Solution :
Let f =
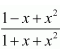
∴By second derivative test,f is the minimum atx= 1 and the minimum value is given by f(1) = 1-1+1/1+1+1 = 1/3
The correct answer is D.
Question
29. The maximum value of
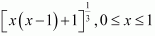is
(A)(1/3)
1/3
(B)1/2
(C) 1
(D) 0
Solution :
Then, we evaluate the value off at critical point x = 1/2 and at the end points of the interval [0, 1] {i.e., atx = 0 andx = 1}.
Hence, we can conclude that the maximum value off in the interval [0, 1] is 1.
The correct answer is C.
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5 FAQs
How many exercise are there in application of derivatives?
Class 12 Maths Chapter 6 Application of Derivatives has 102 questions in 6 exercises along with 24 more provided in a miscellaneous exercise.
What are the applications of derivatives?
To calculate the profit and loss in business using graphs. To check the temperature variation.
What is the full form of AOD in maths?
AOD stands for Application of Derivatives.
Which chapter is required for application of derivatives?
In chapter 6, we are going to learn how to determine the rate of change of quantity, finding the equations of tangents, finding turning points on the graphs for various functions, maxima and minima and so on.
What is the basic rule of derivatives?
The Sum rule says the derivative of a sum of functions is the sum of their derivatives. The Difference rule says the derivative of a difference of functions is the difference of their derivatives.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.